4.3 平行线的性质 课件(共22张PPT)
文档属性
| 名称 | 4.3 平行线的性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
4.3
平行线的性质
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
经历探索平行线性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
【过程与方法】
经历观察、测量、推理、交流等活动,进一步发展空间观念,有条理地思考和表达自己的探索过程和结果,从而进一步增强分析、概括、表达能力.
【情感态度】
在自己独立思考的基础上,积极参与小组活动.在对平行线的性质进行的讨论中,敢于发表自己的看法,并从中获益.
【教学重点】
平行线的三条性质及简单应用.
【教学难点】
平行线的三条性质及简单应用.
情境导入
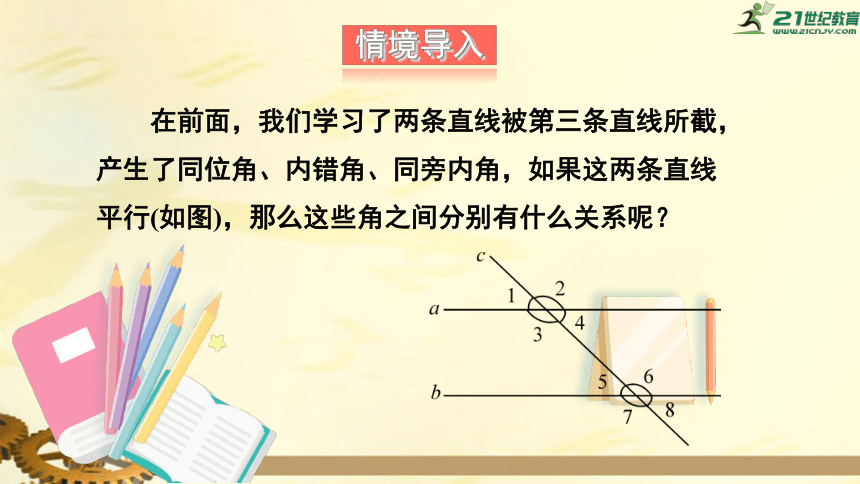
在前面,我们学习了两条直线被第三条直线所截,产生了同位角、内错角、同旁内角,如果这两条直线平行(如图),那么这些角之间分别有什么关系呢?
在图
4-20
和图
4-21
中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
=
=
根据这些操作,
你能猜想出什么结论?
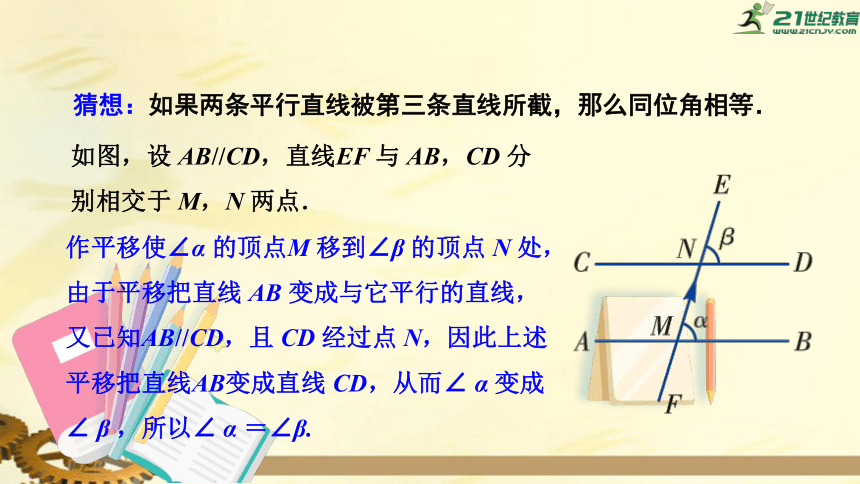
猜想:如果两条平行直线被第三条直线所截,那么同位角相等.
如图,设
AB//CD,直线EF
与
AB,CD
分别相交于
M,N
两点.
作平移使∠α
的顶点M
移到∠β
的顶点
N
处,由于平移把直线
AB
变成与它平行的直线,又已知AB//CD,且
CD
经过点
N,因此上述平移把直线AB变成直线
CD,从而∠
α
变成∠
β
,所以∠
α
=∠β.
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
两条平行直线被第三条直线所截,内错角相等吗?同旁内角互补吗?
如图,平行直线
AB,CD
被直线
EF
所截,∠1与∠2是内错角,∠1与∠3是同旁内角.
因为
AB∥CD,
所以∠1
=∠4(两条平行直线被第三条直线所截,同位角相等).
又因为∠2
=∠4
(对顶角相等),
所以∠1
=∠2
(等量代换).
平行线的性质2
两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
两条平行直线被第三条直线所截,内错角相等吗?同旁内角互补吗?
如图,平行直线
AB,CD
被直线
EF
所截,∠1与∠2是内错角,∠1与∠3是同旁内角.
因为
AB∥CD,
所以∠1
=∠4(两条平行直线被第三条直线所截,同位角相等).
又因为∠3
+∠4
=
180°,
所以∠1
+∠3
=
180°
(等量代换).
平行线的性质3
两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
归纳
如图,
直线
AB,CD
被直线
EF
所截,
AB∥CD,∠1
=
100°,试求∠3的度数.
解
因为
AB∥CD,
所以∠1
=∠2
=
100°(两直线平行,同位角相等).
又因为∠2
+∠3
=
180°,
所以∠3
=
180°
-∠2
=
180°
-
100°
=
80°.
在例
1
中,你能分别用平行线的性质
2
和性质
3
求出∠3
的度数吗?
4
解
因为
AB∥CD,
所以∠1
=∠4
=
100°(两直线平行,内错角相等).
又因为∠3
+∠4
=
180°,
所以∠3
=
180°
-∠4
=
180°
-
100°
=
80°.
在例
1
中,你能分别用平行线的性质
2
和性质
3
求出∠3
的度数吗?
5
解
因为
AB∥CD,
所以∠5
=180°-∠1
=
80°(两直线平行,同旁内角互补).
又因为∠3
=∠5
,(对顶角相等)
所以∠5
=
80°(等量代换).
如图,AD∥BC,∠B
=
∠D,试问
∠A
与∠C
相等吗?为什么?
解
因为
AD∥BC,
所以∠A
+∠B
=
180°,
∠D
+∠C
=
180°
(两直线平行,
同旁内角互补).
又因为∠B
=∠D
(已知),
所以∠A
=∠C.
练
习
1.
如图,AB∥CD,
CD∥EF,
BC∥ED,
∠B
=
70°,求∠C,∠D
和
∠E
的度数.
解:
因为AB∥CD,所以
∠C
=∠B
=
70°,
因为
BC∥ED,
所以
∠C
+
∠D
=180°,
所以
∠D
=110°,
因为
CD∥EF,
所以
∠E
=∠D
=
110°.
2.
如图,直线
AB,CD
被直线
AE
所截,AB∥CD,∠1
=
105°.
求∠2,∠3,∠4
的度数.
解
因为
AB∥CD,
所以∠2
=∠1
=
105°,(两直线平行,
内错角相等)
所以∠3
=180°-∠1=75°,(两直线平行,同旁内角互补).
所以∠4
=∠1
=
105°
,(两直线平行,
同位角相等)
随堂演练
1.如图,一把长方形直尺沿直线断开并错位,点
E、D、B、F在同一条直线上,若∠ADE=125°,则∠DBC的度数为
(
)
A.55°
B.65°
C.75°
D.125°
A
2.
如图,AB∥CD,BF∥CE,则∠B
与∠C有什么关系?请说明理由.
解:因为AB∥CD,
所以∠B
=∠1.
因为BF∥CE,
所以∠C
=∠2.
因为∠1
+∠2
=
180°,
所以∠B
+∠C
=
180°.
即∠B
与∠C
互补.
课堂小结
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
4.3
平行线的性质
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
经历探索平行线性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
【过程与方法】
经历观察、测量、推理、交流等活动,进一步发展空间观念,有条理地思考和表达自己的探索过程和结果,从而进一步增强分析、概括、表达能力.
【情感态度】
在自己独立思考的基础上,积极参与小组活动.在对平行线的性质进行的讨论中,敢于发表自己的看法,并从中获益.
【教学重点】
平行线的三条性质及简单应用.
【教学难点】
平行线的三条性质及简单应用.
情境导入
在前面,我们学习了两条直线被第三条直线所截,产生了同位角、内错角、同旁内角,如果这两条直线平行(如图),那么这些角之间分别有什么关系呢?
在图
4-20
和图
4-21
中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
=
=
根据这些操作,
你能猜想出什么结论?
猜想:如果两条平行直线被第三条直线所截,那么同位角相等.
如图,设
AB//CD,直线EF
与
AB,CD
分别相交于
M,N
两点.
作平移使∠α
的顶点M
移到∠β
的顶点
N
处,由于平移把直线
AB
变成与它平行的直线,又已知AB//CD,且
CD
经过点
N,因此上述平移把直线AB变成直线
CD,从而∠
α
变成∠
β
,所以∠
α
=∠β.
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
两条平行直线被第三条直线所截,内错角相等吗?同旁内角互补吗?
如图,平行直线
AB,CD
被直线
EF
所截,∠1与∠2是内错角,∠1与∠3是同旁内角.
因为
AB∥CD,
所以∠1
=∠4(两条平行直线被第三条直线所截,同位角相等).
又因为∠2
=∠4
(对顶角相等),
所以∠1
=∠2
(等量代换).
平行线的性质2
两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
两条平行直线被第三条直线所截,内错角相等吗?同旁内角互补吗?
如图,平行直线
AB,CD
被直线
EF
所截,∠1与∠2是内错角,∠1与∠3是同旁内角.
因为
AB∥CD,
所以∠1
=∠4(两条平行直线被第三条直线所截,同位角相等).
又因为∠3
+∠4
=
180°,
所以∠1
+∠3
=
180°
(等量代换).
平行线的性质3
两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
归纳
如图,
直线
AB,CD
被直线
EF
所截,
AB∥CD,∠1
=
100°,试求∠3的度数.
解
因为
AB∥CD,
所以∠1
=∠2
=
100°(两直线平行,同位角相等).
又因为∠2
+∠3
=
180°,
所以∠3
=
180°
-∠2
=
180°
-
100°
=
80°.
在例
1
中,你能分别用平行线的性质
2
和性质
3
求出∠3
的度数吗?
4
解
因为
AB∥CD,
所以∠1
=∠4
=
100°(两直线平行,内错角相等).
又因为∠3
+∠4
=
180°,
所以∠3
=
180°
-∠4
=
180°
-
100°
=
80°.
在例
1
中,你能分别用平行线的性质
2
和性质
3
求出∠3
的度数吗?
5
解
因为
AB∥CD,
所以∠5
=180°-∠1
=
80°(两直线平行,同旁内角互补).
又因为∠3
=∠5
,(对顶角相等)
所以∠5
=
80°(等量代换).
如图,AD∥BC,∠B
=
∠D,试问
∠A
与∠C
相等吗?为什么?
解
因为
AD∥BC,
所以∠A
+∠B
=
180°,
∠D
+∠C
=
180°
(两直线平行,
同旁内角互补).
又因为∠B
=∠D
(已知),
所以∠A
=∠C.
练
习
1.
如图,AB∥CD,
CD∥EF,
BC∥ED,
∠B
=
70°,求∠C,∠D
和
∠E
的度数.
解:
因为AB∥CD,所以
∠C
=∠B
=
70°,
因为
BC∥ED,
所以
∠C
+
∠D
=180°,
所以
∠D
=110°,
因为
CD∥EF,
所以
∠E
=∠D
=
110°.
2.
如图,直线
AB,CD
被直线
AE
所截,AB∥CD,∠1
=
105°.
求∠2,∠3,∠4
的度数.
解
因为
AB∥CD,
所以∠2
=∠1
=
105°,(两直线平行,
内错角相等)
所以∠3
=180°-∠1=75°,(两直线平行,同旁内角互补).
所以∠4
=∠1
=
105°
,(两直线平行,
同位角相等)
随堂演练
1.如图,一把长方形直尺沿直线断开并错位,点
E、D、B、F在同一条直线上,若∠ADE=125°,则∠DBC的度数为
(
)
A.55°
B.65°
C.75°
D.125°
A
2.
如图,AB∥CD,BF∥CE,则∠B
与∠C有什么关系?请说明理由.
解:因为AB∥CD,
所以∠B
=∠1.
因为BF∥CE,
所以∠C
=∠2.
因为∠1
+∠2
=
180°,
所以∠B
+∠C
=
180°.
即∠B
与∠C
互补.
课堂小结
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
