第4章 相交线与平行线 复习题4 习题课件(共24张PPT)
文档属性
| 名称 | 第4章 相交线与平行线 复习题4 习题课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 10:21:06 | ||
图片预览








文档简介
(共24张PPT)
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
[选自教材P108]
×
×
[选自教材P108]
解:
对顶角:∠2
和∠4,∠1
和∠3.
同位角:
∠1
和∠5,
∠1
和∠8,
∠4
和∠6,
∠2
和∠7,∠5
和∠7,∠6
和∠8.
内错角:∠2
和∠6,∠3
和∠8,∠4
和∠7,∠5
和∠3.
同旁内角:∠6
和∠3,∠7
和∠3,∠4
和∠8,∠2
和∠5,∠6和∠7.
[选自教材P108]
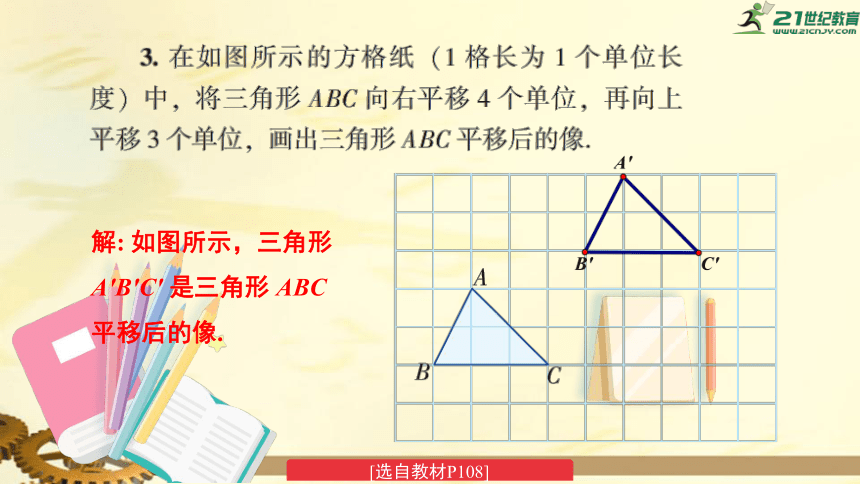
解:
如图所示,三角形A′B′C′
是三角形
ABC平移后的像.
解:
因为
AB∥CD,
∠DCE
=
78°,
所以∠B
=∠DCE
=
78°.
因为
AD∥BE
,
所以∠D
=∠DCE
=78°,
∠A+∠B
=180°,
所以∠A
=180°-∠B
=180°-78°
=102°,
所以∠A,∠B,∠D
的度数分别为
102°,78°,78°.
[选自教材P108]
解:(1)答案不唯一,例如:∠1=∠2,则
a∥b,
理由:同位角相等,两直线平行;
或∠2=∠3,则a∥b,理由:内错角相等,两直线平行;
或∠3+∠4=180°,则a∥b,理由:
同旁内角互补,两直线平行;
或∠5+∠6=180°,则a∥b,理由:如果∠5+∠6
=
180°,那么∠5
与∠6
的对顶角之和等于180°,即同旁内角互补,两直线平行,则
a∥b.
[选自教材P108]
(2)答案不唯一.如∠3=∠5,则
c∥d,
理由:
同位角相等,两直线平行,
或∠4=∠6,则
c∥d,理由:内错角相等,两直线平行,
或∠1=∠5,则
c∥d,理由:如果∠1
=
∠5,且∠1
=
∠3,那么∠3=∠5,
即同位角相等,两直线平行,则
c∥d,
或∠2+∠6=180°,则
c∥d,理由:如果∠2+∠6=180°,那么∠6
与∠2
的对顶角之和等于180°,即同旁内角互补,两直线平行,则
c∥d.
[选自教材P108]
解:因为∠1=∠2,
所以
AB∥DC,
所以∠A+∠ADC
=180°.
因为∠A
=65°,
所以∠ADC
=180°-∠A
=180°-65°
=115°.
[选自教材P108]
[选自教材P109]
已知
等式的基本性质
同位角相等,两直线平行
解:
根据题意知,在点
A
与点
B
处的正北方向是平行的,
所以
30°+∠ABC+60°
=180°,
所以∠ABC
=90°,
所以
CB⊥AB.
因为BC
=12
m,
所以点
C
到直线
AB
的距离是线段
CB
的长度,
即
12
m.
[选自教材P109]
解:
(1)如下图所示.
(2)如下图所示.
[选自教材P109]
解:
因为
a∥b∥c,AB⊥a,AB⊥b,
a
与
b
的距离是
5
cm,
b
与
c
的距离是
2
cm,即
AB
=
5
cm,
BC
=2
cm,所以
AC
=AB
-
BC
=5-2=3
(cm).
所以
a
与
c
的距离为
3
cm.
[选自教材P109]
[选自教材P109]
解:先画出两电线杆的公垂线段,量得长为2.6cm,由比例尺1∶500,计算得1300cm,即两电线杆之间的距离为13m.
[选自教材P110]
解:
(1)BD∥l1
.
(2)因为
l1⊥AB,BD∥l1,
所以
BD⊥AB,所以∠ABD
=90°,
所以∠DBC
=∠ABC-∠ABD
=120°-90°=30°.
因为
BD∥l2,所以∠α
=∠DBC
=30°.
[选自教材P110]
∠DAE
两直线平行,同位角相等
∠EAC
两直线平行,内错角相等
∠DAE
∠EAC
角平分线定义
[选自教材P110]
解:
作一条直线分别于
a,
b
相交,
找出一对同位角,
用量
角器进行测量,
如果两角相等,
则
a∥b
(答案不唯一).
[选自教材P110]
解:
AB∥CD.
理由如下:
因为
OB,
OD
分别平分∠ABD,∠BDC,
所以∠1=∠ABO,
∠2=∠CDO.
又因为∠1+∠2=90°,
所以∠ABD+∠BDC
=∠ABO+∠1+∠CDO+∠2=180°.
所以
AB∥CD.
[选自教材P111]
解:因为
OF⊥CD,所以∠COF
=∠DOF
=90°.
因为∠AOF
=25°,
所以∠AOD
=∠AOF+∠FOD
=25°+90°
=115°,
所以∠BOC
=∠AOD
=115°.
又因为∠COF
=90°,∠AOF
=25°,
所以∠AOC
=90°-25°
=65°,所以∠DOB
=∠AOC
=65°.
因为
OE⊥AB,所以∠EOB
=90°,
所以∠EOD
=∠EOB-∠DOB
=90°-65°
=25°.
[选自教材P111]
解:如右图所示,
过点
E
作
EF∥AB,
所以∠A+∠AEF
=180°.
又因为
AB∥CD,
所以
EF∥CD,
所以∠C+∠CEF
=180°,
所以∠A+∠AEC+∠C
=∠A+∠AEF+∠CEF+∠C
=
180°
+180°
=360°.
[选自教材P111]
[选自教材P111]
略.
提示:
图中的平行线和垂线可根据平行线、垂线的概念进行判断.请自己动手设计一些图案.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
[选自教材P108]
×
×
[选自教材P108]
解:
对顶角:∠2
和∠4,∠1
和∠3.
同位角:
∠1
和∠5,
∠1
和∠8,
∠4
和∠6,
∠2
和∠7,∠5
和∠7,∠6
和∠8.
内错角:∠2
和∠6,∠3
和∠8,∠4
和∠7,∠5
和∠3.
同旁内角:∠6
和∠3,∠7
和∠3,∠4
和∠8,∠2
和∠5,∠6和∠7.
[选自教材P108]
解:
如图所示,三角形A′B′C′
是三角形
ABC平移后的像.
解:
因为
AB∥CD,
∠DCE
=
78°,
所以∠B
=∠DCE
=
78°.
因为
AD∥BE
,
所以∠D
=∠DCE
=78°,
∠A+∠B
=180°,
所以∠A
=180°-∠B
=180°-78°
=102°,
所以∠A,∠B,∠D
的度数分别为
102°,78°,78°.
[选自教材P108]
解:(1)答案不唯一,例如:∠1=∠2,则
a∥b,
理由:同位角相等,两直线平行;
或∠2=∠3,则a∥b,理由:内错角相等,两直线平行;
或∠3+∠4=180°,则a∥b,理由:
同旁内角互补,两直线平行;
或∠5+∠6=180°,则a∥b,理由:如果∠5+∠6
=
180°,那么∠5
与∠6
的对顶角之和等于180°,即同旁内角互补,两直线平行,则
a∥b.
[选自教材P108]
(2)答案不唯一.如∠3=∠5,则
c∥d,
理由:
同位角相等,两直线平行,
或∠4=∠6,则
c∥d,理由:内错角相等,两直线平行,
或∠1=∠5,则
c∥d,理由:如果∠1
=
∠5,且∠1
=
∠3,那么∠3=∠5,
即同位角相等,两直线平行,则
c∥d,
或∠2+∠6=180°,则
c∥d,理由:如果∠2+∠6=180°,那么∠6
与∠2
的对顶角之和等于180°,即同旁内角互补,两直线平行,则
c∥d.
[选自教材P108]
解:因为∠1=∠2,
所以
AB∥DC,
所以∠A+∠ADC
=180°.
因为∠A
=65°,
所以∠ADC
=180°-∠A
=180°-65°
=115°.
[选自教材P108]
[选自教材P109]
已知
等式的基本性质
同位角相等,两直线平行
解:
根据题意知,在点
A
与点
B
处的正北方向是平行的,
所以
30°+∠ABC+60°
=180°,
所以∠ABC
=90°,
所以
CB⊥AB.
因为BC
=12
m,
所以点
C
到直线
AB
的距离是线段
CB
的长度,
即
12
m.
[选自教材P109]
解:
(1)如下图所示.
(2)如下图所示.
[选自教材P109]
解:
因为
a∥b∥c,AB⊥a,AB⊥b,
a
与
b
的距离是
5
cm,
b
与
c
的距离是
2
cm,即
AB
=
5
cm,
BC
=2
cm,所以
AC
=AB
-
BC
=5-2=3
(cm).
所以
a
与
c
的距离为
3
cm.
[选自教材P109]
[选自教材P109]
解:先画出两电线杆的公垂线段,量得长为2.6cm,由比例尺1∶500,计算得1300cm,即两电线杆之间的距离为13m.
[选自教材P110]
解:
(1)BD∥l1
.
(2)因为
l1⊥AB,BD∥l1,
所以
BD⊥AB,所以∠ABD
=90°,
所以∠DBC
=∠ABC-∠ABD
=120°-90°=30°.
因为
BD∥l2,所以∠α
=∠DBC
=30°.
[选自教材P110]
∠DAE
两直线平行,同位角相等
∠EAC
两直线平行,内错角相等
∠DAE
∠EAC
角平分线定义
[选自教材P110]
解:
作一条直线分别于
a,
b
相交,
找出一对同位角,
用量
角器进行测量,
如果两角相等,
则
a∥b
(答案不唯一).
[选自教材P110]
解:
AB∥CD.
理由如下:
因为
OB,
OD
分别平分∠ABD,∠BDC,
所以∠1=∠ABO,
∠2=∠CDO.
又因为∠1+∠2=90°,
所以∠ABD+∠BDC
=∠ABO+∠1+∠CDO+∠2=180°.
所以
AB∥CD.
[选自教材P111]
解:因为
OF⊥CD,所以∠COF
=∠DOF
=90°.
因为∠AOF
=25°,
所以∠AOD
=∠AOF+∠FOD
=25°+90°
=115°,
所以∠BOC
=∠AOD
=115°.
又因为∠COF
=90°,∠AOF
=25°,
所以∠AOC
=90°-25°
=65°,所以∠DOB
=∠AOC
=65°.
因为
OE⊥AB,所以∠EOB
=90°,
所以∠EOD
=∠EOB-∠DOB
=90°-65°
=25°.
[选自教材P111]
解:如右图所示,
过点
E
作
EF∥AB,
所以∠A+∠AEF
=180°.
又因为
AB∥CD,
所以
EF∥CD,
所以∠C+∠CEF
=180°,
所以∠A+∠AEC+∠C
=∠A+∠AEF+∠CEF+∠C
=
180°
+180°
=360°.
[选自教材P111]
[选自教材P111]
略.
提示:
图中的平行线和垂线可根据平行线、垂线的概念进行判断.请自己动手设计一些图案.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
