4.4 平行线的判定 习题课件(共12张PPT)
文档属性
| 名称 | 4.4 平行线的判定 习题课件(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 10:35:58 | ||
图片预览



文档简介
(共12张PPT)
第4章
相交线与平行线
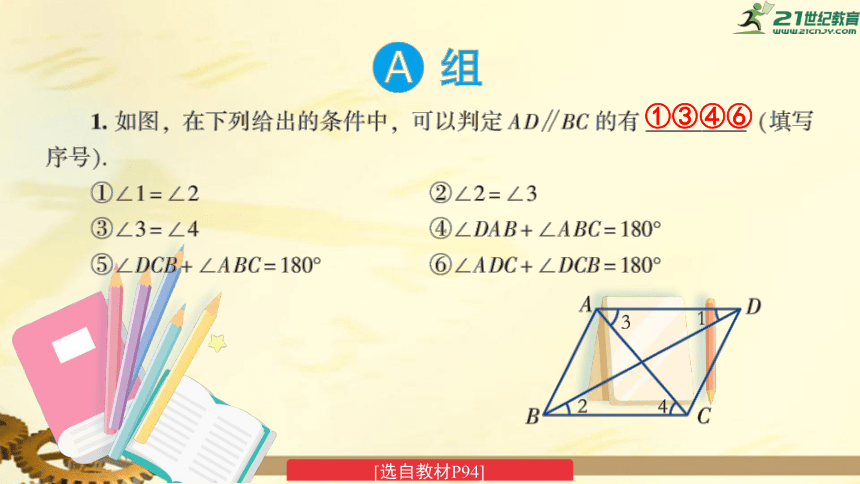
[选自教材P94]
①③④⑥
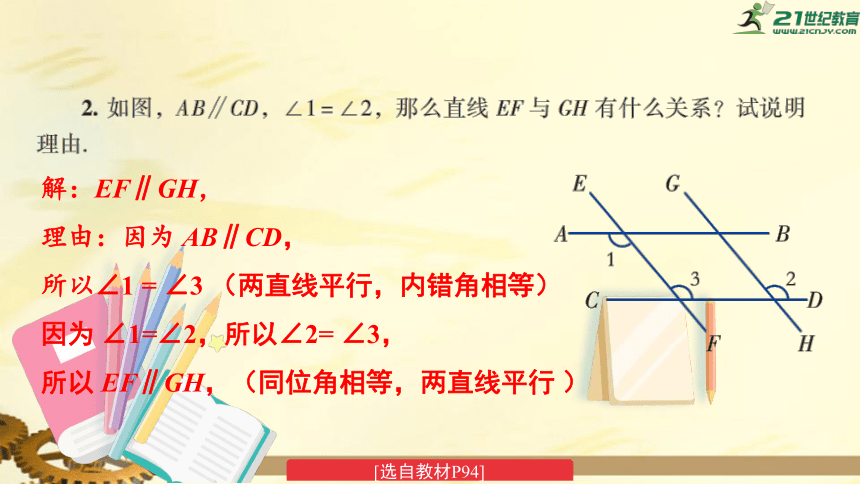
解:EF∥GH,
理由:因为
AB∥CD,
所以∠1
=
∠3
(两直线平行,内错角相等)
因为
∠1=∠2,所以∠2=
∠3,
所以
EF∥GH,(同位角相等,两直线平行
)
[选自教材P94]
两直线平行,同位角相等
同位角相等,两直线平行
[选自教材P95]
[选自教材P95]
解:AC∥BD
.
理由:因为∠1=∠2
所以
AC∥BD,(内错角相等,两直线平行)
AB∥CD.
理由:因为
CB
平分∠ACD
与∠ABD,
所以∠BCD
=∠1
,∠ABC
=∠2,
因为∠1=∠2,所以
∠
BCD
=
∠ABC,
所以
AB∥CD
.(内错角相等,两直线平行)
[选自教材P95]
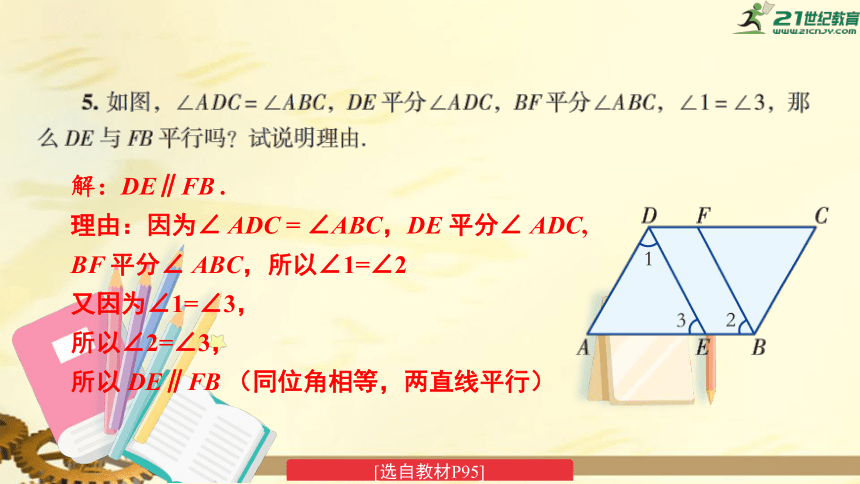
解:DE∥FB
.
理由:因为∠
ADC
=
∠ABC,DE
平分∠
ADC,
BF
平分∠
ABC,所以∠1=∠2
又因为∠1=∠3,
所以∠2=∠3,
所以
DE∥FB
(同位角相等,两直线平行)
[选自教材P95]
解:
答案不唯一.
可以延长阅读栏的边,使它与墙边相交,检查相交成的角是否为直角,如延长
DC
交
AB
于点
E,若∠AEC=90°,则阅读栏的边与墙平行,否则不平行,如右图所示.
[选自教材P95]
解:
AB∥CD.
理由:
因为∠1
与∠3
互余,
所以∠3
的余角是∠1.
又因为∠2
与∠3
的余角互补,
所以∠2+∠1=180°,
所以
AB∥CD
(同旁内角互补,两直线平行).
解:
(1)能.理由:
因为∠1+∠3=180°,∠3+∠4=180°,
所以∠1=∠4,
所以
AB∥CD
(内错角相等,两直线平行).
(2)能.理由:
因为∠1+∠2=180°,
∠3+∠4=180°,∠2=∠3,所以∠1=∠4.
所以
AB∥CD
(内错角相等,两直线平行).
[选自教材P95]
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第4章
相交线与平行线
[选自教材P94]
①③④⑥
解:EF∥GH,
理由:因为
AB∥CD,
所以∠1
=
∠3
(两直线平行,内错角相等)
因为
∠1=∠2,所以∠2=
∠3,
所以
EF∥GH,(同位角相等,两直线平行
)
[选自教材P94]
两直线平行,同位角相等
同位角相等,两直线平行
[选自教材P95]
[选自教材P95]
解:AC∥BD
.
理由:因为∠1=∠2
所以
AC∥BD,(内错角相等,两直线平行)
AB∥CD.
理由:因为
CB
平分∠ACD
与∠ABD,
所以∠BCD
=∠1
,∠ABC
=∠2,
因为∠1=∠2,所以
∠
BCD
=
∠ABC,
所以
AB∥CD
.(内错角相等,两直线平行)
[选自教材P95]
解:DE∥FB
.
理由:因为∠
ADC
=
∠ABC,DE
平分∠
ADC,
BF
平分∠
ABC,所以∠1=∠2
又因为∠1=∠3,
所以∠2=∠3,
所以
DE∥FB
(同位角相等,两直线平行)
[选自教材P95]
解:
答案不唯一.
可以延长阅读栏的边,使它与墙边相交,检查相交成的角是否为直角,如延长
DC
交
AB
于点
E,若∠AEC=90°,则阅读栏的边与墙平行,否则不平行,如右图所示.
[选自教材P95]
解:
AB∥CD.
理由:
因为∠1
与∠3
互余,
所以∠3
的余角是∠1.
又因为∠2
与∠3
的余角互补,
所以∠2+∠1=180°,
所以
AB∥CD
(同旁内角互补,两直线平行).
解:
(1)能.理由:
因为∠1+∠3=180°,∠3+∠4=180°,
所以∠1=∠4,
所以
AB∥CD
(内错角相等,两直线平行).
(2)能.理由:
因为∠1+∠2=180°,
∠3+∠4=180°,∠2=∠3,所以∠1=∠4.
所以
AB∥CD
(内错角相等,两直线平行).
[选自教材P95]
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
