18.1.1 勾股定理 课件(共29张PPT)
文档属性
| 名称 | 18.1.1 勾股定理 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第
18
章
勾股定理
18.1
勾股定理
第
1
课时
勾股定理
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
能说出勾股定理,并能应用其进行简单的计算和实际运用.
【过程与方法】
经历观察—猜想—归纳—验证的数学发现过程,发展合情推理的能力,体会数形结合和由特殊到一般的数学思想.
【情感态度】
通过对勾股定理历史的了解和实例应用,体会勾股定理的文化价值;通过获得成功的经验和克服困难的经历,增进数学学习的信心.
【教学重点】
探索勾股定理.
【教学难点】
利用数形结合的方法验证勾股定理.
新课导入
毕达哥拉斯在朋友家里做客时,从砖铺成的地面中发现了直角三角形三边的数量关系.
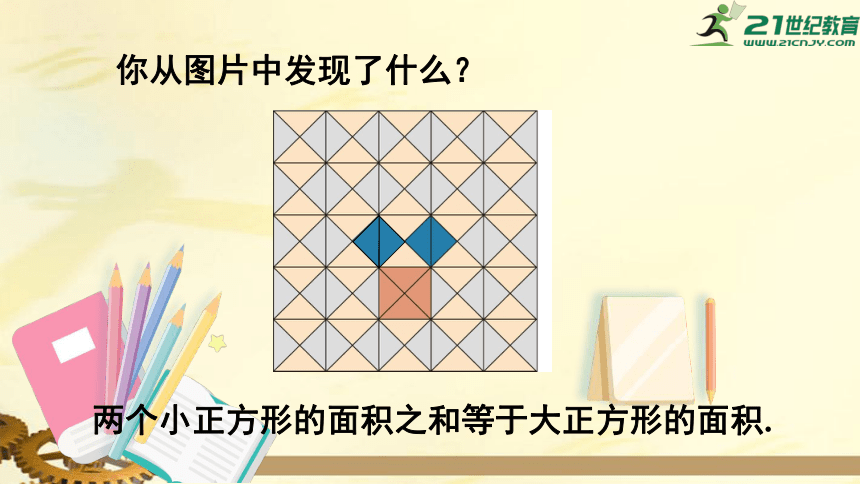
你从图片中发现了什么?
两个小正方形的面积之和等于大正方形的面积.
新课探究
探究
在行距、列距都是
1
的方格网中,任意作出几个以格点为顶点的直角三角形,分别以直角三角形的各边为正方形的一边,向形外作正方形.
(1)
a
b
c
S1
S2
S3
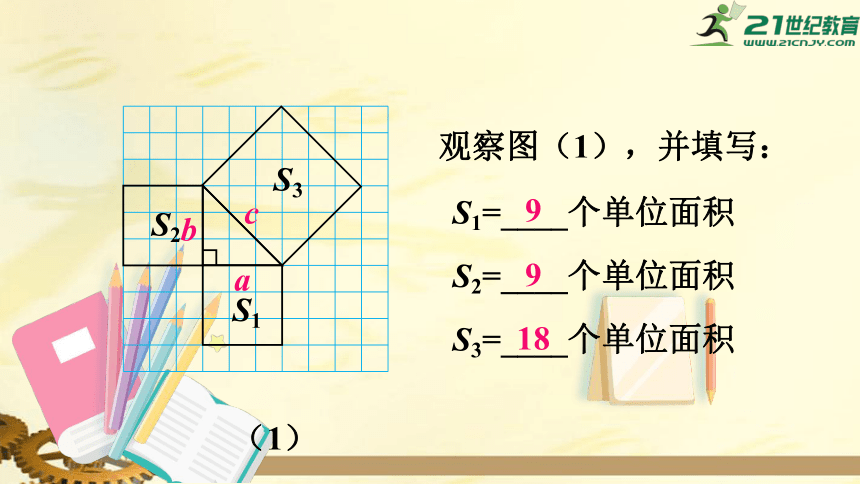
观察图(1),并填写:
S1=____个单位面积
S2=____个单位面积
S3=____个单位面积
9
9
18
(2)
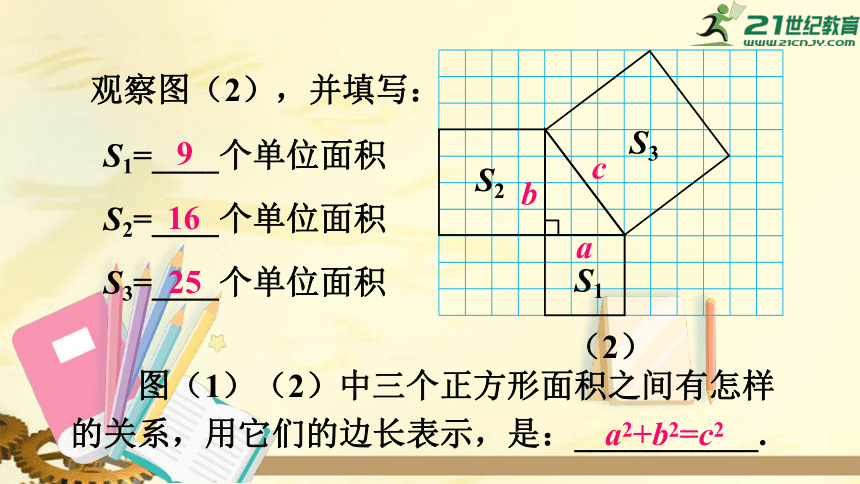
观察图(2),并填写:
S1=____个单位面积
S2=____个单位面积
S3=____个单位面积
9
16
25
a
b
c
S1
S2
S3
图(1)(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是:___________.
a2+b2=c2
定理
直角三角形两条直角边的平方和,等于斜边的平方.
我们称上述定理为勾股定理,国外称为毕达哥拉斯定理.
如果直角三角形的两直角边用
a,b
表示,斜边用
c
表示,那么勾股定理可表示为
a2+b2=c2
涨知识
汉代数学家赵爽把勾股定理叙述成:勾股各自乘,并之为弦实,开方除之即弦.
1.
设直角三角形的两条直角边长分别为
a
和
b,斜边长为
c.
(1)已知
a
=
6,c
=
10,求
b;
(2)已知
a
=
5,b
=
12,求
c;
(3)已知
c
=
25,b
=
15,求
a.
b
=
8
c
=
13
a
=
20
练习
2.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形
A,B,C,D
的边长分别是
12,16,9,12,求最大正方形
E的面积.
解:根据图形正方形E
的边长为:
故E的面积为:252
=
625.
已知:如图(1),在
Rt△ABC
中,∠C
=
90°,AB
=
c,BC
=
a,AC
=
b.
求证:a2
+
b2
=
c2.
(1)
A
C
B
a
b
c
证明:取
4
个与
Rt△ABC
全等的直角三角形,把它们拼成如图(2)所示的边长为
a+b
的正方形EFGH.
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
(2)
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
从图中可见,
A1B1=B1C1=C1D1=A1D1=c.
因为∠B1A1E+∠A1B1E=90°,
而∠A1B1E=∠D1A1H,
因此∠B1A1E+∠D1A1H=90°,
∠D1A1B1=90°.
同理:∠A1B1C1=∠B1C1D1=∠C1D1A1=90°,
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
所以四边形A1B1C1D1是边长为c的正方形.
S正方形EFGH
–
4S△ABC
=S正方形A1B1C1D1,
即(a+b)2
–
4×
ab=c2.
化简,得a2+b2=c2.
1
2
你还有其他的方法证明吗?
b
b
a
a
S=a2+b2
a
c
b
a
c
b
小正方形的面积=
(a-b)2
即c2=a2+b2.
=c2-4×
ab
如图是我国古代证明该命题的“赵爽弦图”.
赵爽弦图
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
你是如何理解的?你会证明吗?
世界上几个文明古国相继发现和研究过勾股定理,据说其证明方法多达
400
多种,有兴趣的同学可以继续研究.
1874年美国总统Garfield证明
A
B
C
D
E
a
b
c
c
a
b
练习
作8个全等的直角三角形(2条直角边长分别为a、b斜边长为
c)再作3个边长分别为
a、b、c
的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗?写出你的验证过程.
解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4×
ab,
由右图可得(a+b)2=c2+4×
ab.
所以a2+b2=c2.
随堂演练
1.在Rt△ABC中,两直角边长分别为3和
,则斜边长为
.
2.在Rt△ABC中,若斜边长为
,一条直角边的长为2,则另一条直角边的长为
.
3.在Rt△ABC中,∠C=90°,a=6,c=10,则b=
.
4.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a=
,∠A=60°,求b,c.
5.已知直角三角形的两边长分别为
3,2,求另一条边长.
解:当斜边的长为3时,另一条边长
当两条直角边长分别为3、2时,斜边长
6.如图,已知长方形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,求DE的长.
解:∵∠A=∠C′=∠C=90°,
∠AEB=∠C′ED,AB=C′D,
∴△AEB≌△C′ED.
∴AE=C′E,
∴C′E=AD-ED=8-ED.
又在△EC′D中,
课堂小结
定理
直角三角形两条直角边的平方和,等于斜边的平方.
a2+b2=c2
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第
18
章
勾股定理
18.1
勾股定理
第
1
课时
勾股定理
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
能说出勾股定理,并能应用其进行简单的计算和实际运用.
【过程与方法】
经历观察—猜想—归纳—验证的数学发现过程,发展合情推理的能力,体会数形结合和由特殊到一般的数学思想.
【情感态度】
通过对勾股定理历史的了解和实例应用,体会勾股定理的文化价值;通过获得成功的经验和克服困难的经历,增进数学学习的信心.
【教学重点】
探索勾股定理.
【教学难点】
利用数形结合的方法验证勾股定理.
新课导入
毕达哥拉斯在朋友家里做客时,从砖铺成的地面中发现了直角三角形三边的数量关系.
你从图片中发现了什么?
两个小正方形的面积之和等于大正方形的面积.
新课探究
探究
在行距、列距都是
1
的方格网中,任意作出几个以格点为顶点的直角三角形,分别以直角三角形的各边为正方形的一边,向形外作正方形.
(1)
a
b
c
S1
S2
S3
观察图(1),并填写:
S1=____个单位面积
S2=____个单位面积
S3=____个单位面积
9
9
18
(2)
观察图(2),并填写:
S1=____个单位面积
S2=____个单位面积
S3=____个单位面积
9
16
25
a
b
c
S1
S2
S3
图(1)(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是:___________.
a2+b2=c2
定理
直角三角形两条直角边的平方和,等于斜边的平方.
我们称上述定理为勾股定理,国外称为毕达哥拉斯定理.
如果直角三角形的两直角边用
a,b
表示,斜边用
c
表示,那么勾股定理可表示为
a2+b2=c2
涨知识
汉代数学家赵爽把勾股定理叙述成:勾股各自乘,并之为弦实,开方除之即弦.
1.
设直角三角形的两条直角边长分别为
a
和
b,斜边长为
c.
(1)已知
a
=
6,c
=
10,求
b;
(2)已知
a
=
5,b
=
12,求
c;
(3)已知
c
=
25,b
=
15,求
a.
b
=
8
c
=
13
a
=
20
练习
2.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形
A,B,C,D
的边长分别是
12,16,9,12,求最大正方形
E的面积.
解:根据图形正方形E
的边长为:
故E的面积为:252
=
625.
已知:如图(1),在
Rt△ABC
中,∠C
=
90°,AB
=
c,BC
=
a,AC
=
b.
求证:a2
+
b2
=
c2.
(1)
A
C
B
a
b
c
证明:取
4
个与
Rt△ABC
全等的直角三角形,把它们拼成如图(2)所示的边长为
a+b
的正方形EFGH.
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
(2)
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
从图中可见,
A1B1=B1C1=C1D1=A1D1=c.
因为∠B1A1E+∠A1B1E=90°,
而∠A1B1E=∠D1A1H,
因此∠B1A1E+∠D1A1H=90°,
∠D1A1B1=90°.
同理:∠A1B1C1=∠B1C1D1=∠C1D1A1=90°,
H
G
E
F
A1
B1
C1
D1
a
a
a
a
b
b
b
b
c
c
c
c
所以四边形A1B1C1D1是边长为c的正方形.
S正方形EFGH
–
4S△ABC
=S正方形A1B1C1D1,
即(a+b)2
–
4×
ab=c2.
化简,得a2+b2=c2.
1
2
你还有其他的方法证明吗?
b
b
a
a
S=a2+b2
a
c
b
a
c
b
小正方形的面积=
(a-b)2
即c2=a2+b2.
=c2-4×
ab
如图是我国古代证明该命题的“赵爽弦图”.
赵爽弦图
赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
你是如何理解的?你会证明吗?
世界上几个文明古国相继发现和研究过勾股定理,据说其证明方法多达
400
多种,有兴趣的同学可以继续研究.
1874年美国总统Garfield证明
A
B
C
D
E
a
b
c
c
a
b
练习
作8个全等的直角三角形(2条直角边长分别为a、b斜边长为
c)再作3个边长分别为
a、b、c
的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗?写出你的验证过程.
解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4×
ab,
由右图可得(a+b)2=c2+4×
ab.
所以a2+b2=c2.
随堂演练
1.在Rt△ABC中,两直角边长分别为3和
,则斜边长为
.
2.在Rt△ABC中,若斜边长为
,一条直角边的长为2,则另一条直角边的长为
.
3.在Rt△ABC中,∠C=90°,a=6,c=10,则b=
.
4.在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a=
,∠A=60°,求b,c.
5.已知直角三角形的两边长分别为
3,2,求另一条边长.
解:当斜边的长为3时,另一条边长
当两条直角边长分别为3、2时,斜边长
6.如图,已知长方形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,求DE的长.
解:∵∠A=∠C′=∠C=90°,
∠AEB=∠C′ED,AB=C′D,
∴△AEB≌△C′ED.
∴AE=C′E,
∴C′E=AD-ED=8-ED.
又在△EC′D中,
课堂小结
定理
直角三角形两条直角边的平方和,等于斜边的平方.
a2+b2=c2
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
