18.1.2 勾股定理的应用 课件(共25张PPT)
文档属性
| 名称 | 18.1.2 勾股定理的应用 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 10:40:19 | ||
图片预览








文档简介
(共25张PPT)
第
2
课时
勾股定理的应用
第18章
勾股定理
18.1
勾股定理
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
掌握勾股定理在实际问题中的应用
【过程与方法】
通过勾股定理在实际问题中的应用,感受勾股定理的应用方法
【情感态度】
培养良好的思维意识,发展数学理念,体会勾股定理的应用价值
【教学重点】
勾股定理的实际应用
【教学难点】
勾股定理的灵活应用
新课导入
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)a=6,b=8,求c;
(2)a=8,c=17,求b.
c=10
b=15
这节课我们就来学习用勾股定理解决实际问题.
提问
新课探究
例1
现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到
10
m,消防车高
3
m.救人时云梯伸至最长,在完成从
9
m
高处救人后,还要从
12
m
高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到
0.1
m)
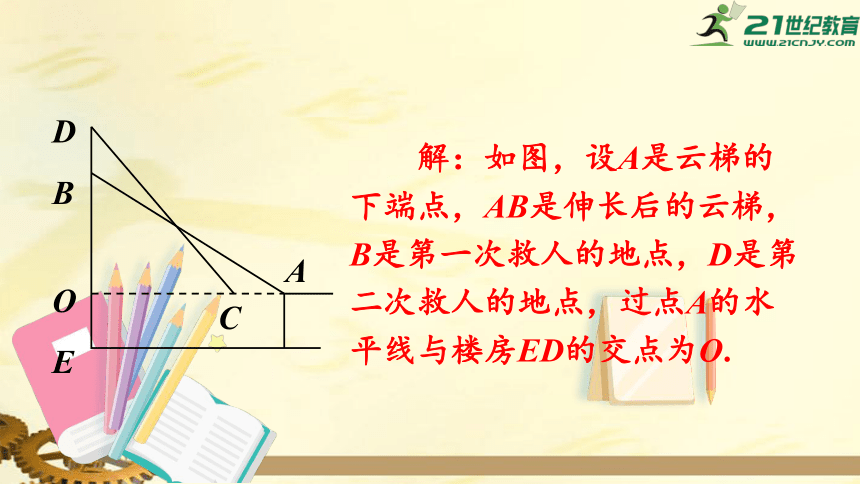
解:如图,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O.
E
D
B
O
A
C
则OB=9–3=6(m),
OD=12–3=9(m).
根据勾股定理,得
AO2=AB2–OB2=102–62=64,
解得
AO=8(m)
设AC=x,则OC=8-x,
E
D
B
O
A
C
于是根据勾股定理,得
OC2+OD2=CD2,
即
(8-x)2+92=102,
解得
x≈3.6
答:消防车要从原处再向着火的楼房靠近约3.6米.
E
D
B
O
A
C
一个门框的尺寸如图所示,一块长3
m,宽2.2
m的长方形薄木板能否从门框内通过?为什么?
练习
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC=
≈2.24.
因为AC大于木板的宽2.2
m,所
以木板能从门框内通过.
例2
已知:如图所示,在Rt△ABC中,两条直角边AC=5,BC=12.
求斜边上的高CD的长.
A
C
B
D
解
在Rt△ABC中,
AB2=AC2+BC2
=52+122=169,
AB=
=13.
又∵Rt△ABC的面积
S△ABC=
AC·BC=
AB·CD,
∴CD
=
=
=
.
1
2
1
2
AC·BC
AB
5×12
13
60
13
A
C
B
D
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60
m,AC=20m.求A,B两点间的距离(结果取整数).
解:
练习
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示
的点吗?
在数轴上找到点A,使OA=3;
作直线l⊥OA,在l上取一点B,使AB=2;
以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点.
1
2
3
A
B
C
O
1
2
3
2
下面都是利用勾股定理画出的美丽图形。
随堂演练
1.求出下列直角三角形中未知的边.
AC=8
AB=17
2.
如图,一架2.6米长的梯子AB
斜靠在一竖直的墙AO上,这时AO
为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
C
O
D
B
A
在Rt△COD中,根据勾股定理,
OD2=CD2–OC2=2.62–(2.4
–
0.5)2=3.15.
解:在Rt△AOB中,根据勾股定理,
OB2=AB2
–
OA2=2.62
–
2.42=1.
OB=1.
3.
如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)AD⊥BC于D,则BD=CD=3.
在Rt△ABD中,由勾股定理
AD2=AB2-BD2=62-32=27,故AD=3
≈5.2
(2)S=
·BC·AD=
×6×3
≈15.6
解:点A即为表示
的点.
4.在数轴上作出表示
的点.
这是我们刚上课时提出的问题,现在你会算了吗?
解:设水深为h尺.
由题意得:AC=3,BC=6,OC=h,
由勾股定理得:
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第
2
课时
勾股定理的应用
第18章
勾股定理
18.1
勾股定理
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
掌握勾股定理在实际问题中的应用
【过程与方法】
通过勾股定理在实际问题中的应用,感受勾股定理的应用方法
【情感态度】
培养良好的思维意识,发展数学理念,体会勾股定理的应用价值
【教学重点】
勾股定理的实际应用
【教学难点】
勾股定理的灵活应用
新课导入
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)a=6,b=8,求c;
(2)a=8,c=17,求b.
c=10
b=15
这节课我们就来学习用勾股定理解决实际问题.
提问
新课探究
例1
现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图,已知云梯最多只能伸长到
10
m,消防车高
3
m.救人时云梯伸至最长,在完成从
9
m
高处救人后,还要从
12
m
高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到
0.1
m)
解:如图,设A是云梯的下端点,AB是伸长后的云梯,B是第一次救人的地点,D是第二次救人的地点,过点A的水平线与楼房ED的交点为O.
E
D
B
O
A
C
则OB=9–3=6(m),
OD=12–3=9(m).
根据勾股定理,得
AO2=AB2–OB2=102–62=64,
解得
AO=8(m)
设AC=x,则OC=8-x,
E
D
B
O
A
C
于是根据勾股定理,得
OC2+OD2=CD2,
即
(8-x)2+92=102,
解得
x≈3.6
答:消防车要从原处再向着火的楼房靠近约3.6米.
E
D
B
O
A
C
一个门框的尺寸如图所示,一块长3
m,宽2.2
m的长方形薄木板能否从门框内通过?为什么?
练习
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC=
≈2.24.
因为AC大于木板的宽2.2
m,所
以木板能从门框内通过.
例2
已知:如图所示,在Rt△ABC中,两条直角边AC=5,BC=12.
求斜边上的高CD的长.
A
C
B
D
解
在Rt△ABC中,
AB2=AC2+BC2
=52+122=169,
AB=
=13.
又∵Rt△ABC的面积
S△ABC=
AC·BC=
AB·CD,
∴CD
=
=
=
.
1
2
1
2
AC·BC
AB
5×12
13
60
13
A
C
B
D
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60
m,AC=20m.求A,B两点间的距离(结果取整数).
解:
练习
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示
的点吗?
在数轴上找到点A,使OA=3;
作直线l⊥OA,在l上取一点B,使AB=2;
以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点.
1
2
3
A
B
C
O
1
2
3
2
下面都是利用勾股定理画出的美丽图形。
随堂演练
1.求出下列直角三角形中未知的边.
AC=8
AB=17
2.
如图,一架2.6米长的梯子AB
斜靠在一竖直的墙AO上,这时AO
为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
C
O
D
B
A
在Rt△COD中,根据勾股定理,
OD2=CD2–OC2=2.62–(2.4
–
0.5)2=3.15.
解:在Rt△AOB中,根据勾股定理,
OB2=AB2
–
OA2=2.62
–
2.42=1.
OB=1.
3.
如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)AD⊥BC于D,则BD=CD=3.
在Rt△ABD中,由勾股定理
AD2=AB2-BD2=62-32=27,故AD=3
≈5.2
(2)S=
·BC·AD=
×6×3
≈15.6
解:点A即为表示
的点.
4.在数轴上作出表示
的点.
这是我们刚上课时提出的问题,现在你会算了吗?
解:设水深为h尺.
由题意得:AC=3,BC=6,OC=h,
由勾股定理得:
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
