北京市良乡第二中学2020-2021学年第二学期九年级数学开学考试试题(word版,含答案)
文档属性
| 名称 | 北京市良乡第二中学2020-2021学年第二学期九年级数学开学考试试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 705.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 11:33:05 | ||
图片预览




文档简介
1118870010795000良乡二中初三数学入学检测2021.3
一、选择题(本题共24分,每小题3分)
1.抛物线false的顶点坐标是( )
A.false B.false C.false D.false
2. 已知△ABC,AC=3,CB=4,以点C为圆心,r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
5119370100330A.r>3 B.r≥4 C.33. 如图,AB为☉O的直径,C为☉O上的一点,过点C作☉O的切线,交直径AB的延长线于点D.若∠A=25°,则∠D的度数是 ( )
A. 25° B. 40° C. 50° D. 65°
5048250438154.点A是函数false(x>0)图象上的一点,过点A分别向x轴,y轴作垂线,垂足为B,C,则四边形ABOC的面积是( )
A.3 B.6 C.12 D.24
5. 若一个扇形的半径是18cm,且它的弧长是12π cm,则此扇形的圆心角等于( )
527685026035A.30° B.60° C.90° D.120°
6.如图,⊙O的直径AB垂直于弦CD,垂足为E.若false,AC=2,则CD的长是( )
A.4 B.false C.2 D.false
7.二次函数y=x2-2x,若A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是 ( )
A.y1y2 D.不能确定
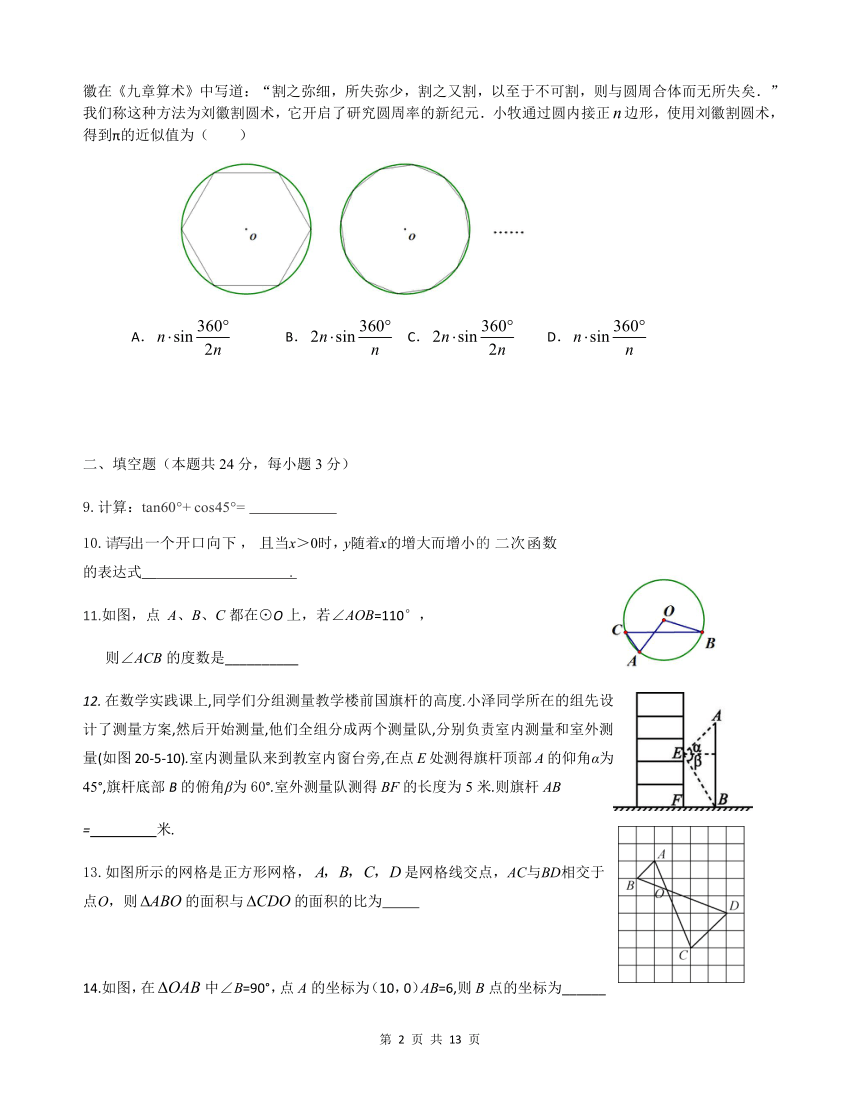
8. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正false边形,使用刘徽割圆术,得到π的近似值为( )
A.false B.false C.false D.false
二、填空题(本题共24分,每小题3分)
9.计算:tan60°+ cos45°=
473773538100010.请写出一个开口向下, 且当x>0时,y随着x的增大而增小的二次函数的表达式 .
11.如图,点 A、B、C都在⊙O上,若∠AOB=110°,
则∠ACB的度数是__________
48444151227455479933013335在数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量,他们全组分成两个测量队,分别负责室内测量和室外测量(如图20-5-10).室内测量队来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°.室外测量队测得BF的长度为5米.则旗杆AB
= 米.?
13.如图所示的网格是正方形网格,false是网格线交点,AC与BD相交于点O,则false的面积与false的面积的比为
14.如图,在false中∠B=90°,点A的坐标为(10,0)AB=6,则B点的坐标为______
9207577470
在平面直角坐标系xOy中,A(-2,m)在反比例函数false(k<0)上,将A点向下平移3个单位得到点B,B点恰在反比例函数false上,则k的值为__________。
16.已知双曲线false与直线false交于点false,false.
(1)若false,则false ;
(2)若false时,false,则k 0,b 0(填“>”、“=”或“<”).
良乡二中初三数学入学检测答题卡 2021.3
一、选择题(本题共24分,每小题3分)
1
2
3
4
5
6
7
8
二、填空题(本题共24分,每小题3分)
9
10
11
12
13
14
15
16
解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)
4289425183515解答应写出文字说明、演算步骤或证明过程.
17.如图,AC平分∠BAD,∠B=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AB=2,AC=3,求AD的长.
18.已知抛物线y=ax2+bx+c(a≠0)图像上部分点的横坐标x与纵坐标y的对应值如下表:
…
…
…
5
0
-3
-4
-3
0
…
(1)求此抛物线的解析式;
(2)画出函数图像,结合图像直接写出当false时,y 的范围.
39008055080
19.已知:如图,直线 l,和直线外一点P.
求作:过点P作直线PC,使得PC∥l,
4068445280035作法:①在直线l上取点false,以点false为圆心,false长为半径画圆,交直线l于A,B两点;
②连接false,以点false为圆心,false长为半径画弧,交半圆于点C;
③作直线false.
直线false即为所求作.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明
证明:连接BP
∵BC=AP
∴false=
∴false∠BPC( )(填推理依据)
∴直线PC∥l.
已知:如图1,△ABC中,tanB=false,BC=6,过点A作BC边上的高,垂足为点D,且满足
BD:CD=2:1,求△ABC的面积.
333375231775
5148580-5715021.如图所示,一次函数false的图象与反比例函数false的图象交于点P,PA⊥false轴于点A,PB⊥false轴于点B,一次函数的图象分别交false轴、false轴于点C、点D,且false,false.
(1)求点D的坐标;
(2)求一次函数与反比例函数的表达式;
(3)根据图象写出当false取何值时,一次函数的值小于反比例函数的值?
414083563500
22.已知:AB为⊙O的直径,点D为弧BC的中点,过点D作⊙O的切线交AB的延长线于点E,连接CB.
(1)求证:BC∥DE;
(2)若cos E=false,E =20,求BC的长.
426339010477523.在平面直角坐标系false中,抛物线false与false轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)①直接写出抛物线的对称轴是________;
②用含a的代数式表示b;
(2)横、纵坐标都是整数的点叫做整点.若抛物线与false轴交于P、Q两点,该抛物线在P、Q之间的部分与线段PQ所围成的区域(不包括边界)恰有七个整点,结合函数图象,求a的取值范围.
24.在△ABC中,AB=AC,∠BAC=90°,点D是线段BC上的动点(BD>CD),作射线AD,点B关于射线AD的对称点为P,作直线CP,交射线AD于点Q.连接AP,BQ.
4387850113665(1)依题意补全图形,直接写出∠AQP的度数;
(2)用等式表示线段AQ,CQ,BQ之间的数量关系,并证明.
46431202540
在平面直角坐标系xOy中,对于点P,若点Q满足条件:以线段PQ为对角线的正方形,边均与某条坐标轴垂直,则称点Q为点P的“正轨点”,该正方形为点P的“正轨正方形”如下图所示.
(1)已知点A的坐标是(1,3).
①在(-3,-1),(2,2),(3,3)中,是点A的“正轨点”的坐标是 .
②若点A的“正轨正方形”的面积是4,写出一个点A的“正轨点”的坐标 .
(2)若点B(1,0)的“正轨点”在直线y=2x+2上,求点B的“正轨点”的坐标;
(3)已知点C(n,0),若直线y=2x+n上存在点C的“正轨点”,使得点C的“正轨正方形”面积小于4,直接写出n的取值范围.
良乡二中初三数学入学检测答案评标2021.3
B 2. C 3.B 4.A 5.D 6. C 7.C 8.A
false (或false)
false (不唯一,只要满足a<0,false即可)
55°
false
false
(6.4,4.8)
-3
(1)0;(2)<;>.(每空1分)
(1)解:∵AC分∠BAD,
∴∠BAC=∠CAD …………………………………………… 1分
∵∠B=∠ACD,
∴ △ABC∽△ACD …………………………………………………………… 2分
∵△ABC∽△ACD
∴ false……………………………………………………………… 3分
∵AB=2 AC=3
∴AD=false ……………………………… 5分
18.解:(1)∵设二次函数的解析式为false
由题意得,false 1
解得,false
∴false 2
(2)画图略 3
false 5
19.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹); 2
3023235189230
(2)完成下面的证明
证明:∵BC=AP
.∴false=false 3
∴false∠BPC( 同弧(或等弧)所对的圆周角相等 )
5
∴直线false.
解:如图1所示:
∵BC=6,BD:CD=2:1,
∴BD=4, --------------------------------------------------------1
∵AD⊥BC,tanB=,
∴=,
∴AD= BD=, --------------------------------------------4
∴S△ABC=BC?AD=×6×=8; ---------------------------------------------------5
21.解:(1)由图象可知,函数false的图象经过点A(1,6),可得false=6.---1
设直线AB的解析式为false.
∵ A(1,6),B(6,1)两点在函数false的图象上,
∴ false 解得false----------------------------------------3
∴ 直线AB的解析式为false.------------------------------------4
(2)题图中阴影部分(不包括边界)所含格点的个数是3.--------------------5
22.
(1)
证明:连结OD.…………………………………………..…………..1分
∵DE切⊙O于点D,
∴OD⊥DE,
又∵点D为弧BC的中点,
∴OD⊥BC,
∴BC∥DE.…………………………………………………………..3分
(2)解:
3467100262890在Rt△OED中,∠ODE=90°,cosE=false,
∴false,
∵DE =20,
∴OE=25,
∴OD=15,AB=30,
∵BC∥DE,
∴∠ABC =∠E,
∴cos ∠ABC=false,…………………………….…….4分
连接AC,
在Rt△ABC中,∠ACB=90°,cos ∠ABC=false,
∴BC=24.……………………………………………..6分
23. (1) ①对称轴是:x=1. …………………………………… 1分
②b=-2a. …………………………………… 3分
(2)由题可知:A(0,3) B(2,3)
①若a>0时
∵-8≤-a+3<-7
∴10<a≤11 ………………………………… 5分
②若a<0时 ……
当x=-1时,y=3a+3
∵恰有7个整数点
∴3a+3≤1-a+3≤4
∴-1≤a≤-23 ………………………………… 7分
24.(1)补图如图;…… 2分
∠AQP=45°……………… 3分
279717597155-105410135890
CQ+BQ=2AQ
延长QB至点M使MB=CQ①
由对称可知:∠ABQ=∠APQ,AB=AP
∵AB=AC
∴AC=AP
∴∠ACP=∠APQ;
∴∠ACP=∠ABQ
∴∠ABM=∠ACQ② ……… 4分
∵AB=AC③
由①②③可知△AMB≌△AQC(SAS) ……… 5分
∴∠MAB=∠QAC AM=AQ
∴∠MAB+∠BAQ=∠BAQ+∠QAC
即∠ MAQ=∠BAC=90° …… 6分
∴MQ=2AQ
即MB+BQ=2AQ
∴CQ+BQ=2AQ …7分
25. (1)①(-3,-1),(2,2)……………………………………………………2分
②(-1,1)……………………………………………………………………...3分
(2)∵点B(1,0)的“正轨点”在直线y=2x+2上,
∴false或false.
∴false或false.……………………………………………………….4分
∴点B的“正轨点”的坐标是false,(-3,-4).………………………...5分
(3)-2<n<2且n≠0…………………….…………………………………..7分
一、选择题(本题共24分,每小题3分)
1.抛物线false的顶点坐标是( )
A.false B.false C.false D.false
2. 已知△ABC,AC=3,CB=4,以点C为圆心,r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是( )
5119370100330A.r>3 B.r≥4 C.3
A. 25° B. 40° C. 50° D. 65°
5048250438154.点A是函数false(x>0)图象上的一点,过点A分别向x轴,y轴作垂线,垂足为B,C,则四边形ABOC的面积是( )
A.3 B.6 C.12 D.24
5. 若一个扇形的半径是18cm,且它的弧长是12π cm,则此扇形的圆心角等于( )
527685026035A.30° B.60° C.90° D.120°
6.如图,⊙O的直径AB垂直于弦CD,垂足为E.若false,AC=2,则CD的长是( )
A.4 B.false C.2 D.false
7.二次函数y=x2-2x,若A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是 ( )
A.y1
8. 公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正false边形,使用刘徽割圆术,得到π的近似值为( )
A.false B.false C.false D.false
二、填空题(本题共24分,每小题3分)
9.计算:tan60°+ cos45°=
473773538100010.请写出一个开口向下, 且当x>0时,y随着x的增大而增小的二次函数的表达式 .
11.如图,点 A、B、C都在⊙O上,若∠AOB=110°,
则∠ACB的度数是__________
48444151227455479933013335在数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量,他们全组分成两个测量队,分别负责室内测量和室外测量(如图20-5-10).室内测量队来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°.室外测量队测得BF的长度为5米.则旗杆AB
= 米.?
13.如图所示的网格是正方形网格,false是网格线交点,AC与BD相交于点O,则false的面积与false的面积的比为
14.如图,在false中∠B=90°,点A的坐标为(10,0)AB=6,则B点的坐标为______
9207577470
在平面直角坐标系xOy中,A(-2,m)在反比例函数false(k<0)上,将A点向下平移3个单位得到点B,B点恰在反比例函数false上,则k的值为__________。
16.已知双曲线false与直线false交于点false,false.
(1)若false,则false ;
(2)若false时,false,则k 0,b 0(填“>”、“=”或“<”).
良乡二中初三数学入学检测答题卡 2021.3
一、选择题(本题共24分,每小题3分)
1
2
3
4
5
6
7
8
二、填空题(本题共24分,每小题3分)
9
10
11
12
13
14
15
16
解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)
4289425183515解答应写出文字说明、演算步骤或证明过程.
17.如图,AC平分∠BAD,∠B=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AB=2,AC=3,求AD的长.
18.已知抛物线y=ax2+bx+c(a≠0)图像上部分点的横坐标x与纵坐标y的对应值如下表:
…
…
…
5
0
-3
-4
-3
0
…
(1)求此抛物线的解析式;
(2)画出函数图像,结合图像直接写出当false时,y 的范围.
39008055080
19.已知:如图,直线 l,和直线外一点P.
求作:过点P作直线PC,使得PC∥l,
4068445280035作法:①在直线l上取点false,以点false为圆心,false长为半径画圆,交直线l于A,B两点;
②连接false,以点false为圆心,false长为半径画弧,交半圆于点C;
③作直线false.
直线false即为所求作.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明
证明:连接BP
∵BC=AP
∴false=
∴false∠BPC( )(填推理依据)
∴直线PC∥l.
已知:如图1,△ABC中,tanB=false,BC=6,过点A作BC边上的高,垂足为点D,且满足
BD:CD=2:1,求△ABC的面积.
333375231775
5148580-5715021.如图所示,一次函数false的图象与反比例函数false的图象交于点P,PA⊥false轴于点A,PB⊥false轴于点B,一次函数的图象分别交false轴、false轴于点C、点D,且false,false.
(1)求点D的坐标;
(2)求一次函数与反比例函数的表达式;
(3)根据图象写出当false取何值时,一次函数的值小于反比例函数的值?
414083563500
22.已知:AB为⊙O的直径,点D为弧BC的中点,过点D作⊙O的切线交AB的延长线于点E,连接CB.
(1)求证:BC∥DE;
(2)若cos E=false,E =20,求BC的长.
426339010477523.在平面直角坐标系false中,抛物线false与false轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)①直接写出抛物线的对称轴是________;
②用含a的代数式表示b;
(2)横、纵坐标都是整数的点叫做整点.若抛物线与false轴交于P、Q两点,该抛物线在P、Q之间的部分与线段PQ所围成的区域(不包括边界)恰有七个整点,结合函数图象,求a的取值范围.
24.在△ABC中,AB=AC,∠BAC=90°,点D是线段BC上的动点(BD>CD),作射线AD,点B关于射线AD的对称点为P,作直线CP,交射线AD于点Q.连接AP,BQ.
4387850113665(1)依题意补全图形,直接写出∠AQP的度数;
(2)用等式表示线段AQ,CQ,BQ之间的数量关系,并证明.
46431202540
在平面直角坐标系xOy中,对于点P,若点Q满足条件:以线段PQ为对角线的正方形,边均与某条坐标轴垂直,则称点Q为点P的“正轨点”,该正方形为点P的“正轨正方形”如下图所示.
(1)已知点A的坐标是(1,3).
①在(-3,-1),(2,2),(3,3)中,是点A的“正轨点”的坐标是 .
②若点A的“正轨正方形”的面积是4,写出一个点A的“正轨点”的坐标 .
(2)若点B(1,0)的“正轨点”在直线y=2x+2上,求点B的“正轨点”的坐标;
(3)已知点C(n,0),若直线y=2x+n上存在点C的“正轨点”,使得点C的“正轨正方形”面积小于4,直接写出n的取值范围.
良乡二中初三数学入学检测答案评标2021.3
B 2. C 3.B 4.A 5.D 6. C 7.C 8.A
false (或false)
false (不唯一,只要满足a<0,false即可)
55°
false
false
(6.4,4.8)
-3
(1)0;(2)<;>.(每空1分)
(1)解:∵AC分∠BAD,
∴∠BAC=∠CAD …………………………………………… 1分
∵∠B=∠ACD,
∴ △ABC∽△ACD …………………………………………………………… 2分
∵△ABC∽△ACD
∴ false……………………………………………………………… 3分
∵AB=2 AC=3
∴AD=false ……………………………… 5分
18.解:(1)∵设二次函数的解析式为false
由题意得,false 1
解得,false
∴false 2
(2)画图略 3
false 5
19.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹); 2
3023235189230
(2)完成下面的证明
证明:∵BC=AP
.∴false=false 3
∴false∠BPC( 同弧(或等弧)所对的圆周角相等 )
5
∴直线false.
解:如图1所示:
∵BC=6,BD:CD=2:1,
∴BD=4, --------------------------------------------------------1
∵AD⊥BC,tanB=,
∴=,
∴AD= BD=, --------------------------------------------4
∴S△ABC=BC?AD=×6×=8; ---------------------------------------------------5
21.解:(1)由图象可知,函数false的图象经过点A(1,6),可得false=6.---1
设直线AB的解析式为false.
∵ A(1,6),B(6,1)两点在函数false的图象上,
∴ false 解得false----------------------------------------3
∴ 直线AB的解析式为false.------------------------------------4
(2)题图中阴影部分(不包括边界)所含格点的个数是3.--------------------5
22.
(1)
证明:连结OD.…………………………………………..…………..1分
∵DE切⊙O于点D,
∴OD⊥DE,
又∵点D为弧BC的中点,
∴OD⊥BC,
∴BC∥DE.…………………………………………………………..3分
(2)解:
3467100262890在Rt△OED中,∠ODE=90°,cosE=false,
∴false,
∵DE =20,
∴OE=25,
∴OD=15,AB=30,
∵BC∥DE,
∴∠ABC =∠E,
∴cos ∠ABC=false,…………………………….…….4分
连接AC,
在Rt△ABC中,∠ACB=90°,cos ∠ABC=false,
∴BC=24.……………………………………………..6分
23. (1) ①对称轴是:x=1. …………………………………… 1分
②b=-2a. …………………………………… 3分
(2)由题可知:A(0,3) B(2,3)
①若a>0时
∵-8≤-a+3<-7
∴10<a≤11 ………………………………… 5分
②若a<0时 ……
当x=-1时,y=3a+3
∵恰有7个整数点
∴3a+3≤1-a+3≤4
∴-1≤a≤-23 ………………………………… 7分
24.(1)补图如图;…… 2分
∠AQP=45°……………… 3分
279717597155-105410135890
CQ+BQ=2AQ
延长QB至点M使MB=CQ①
由对称可知:∠ABQ=∠APQ,AB=AP
∵AB=AC
∴AC=AP
∴∠ACP=∠APQ;
∴∠ACP=∠ABQ
∴∠ABM=∠ACQ② ……… 4分
∵AB=AC③
由①②③可知△AMB≌△AQC(SAS) ……… 5分
∴∠MAB=∠QAC AM=AQ
∴∠MAB+∠BAQ=∠BAQ+∠QAC
即∠ MAQ=∠BAC=90° …… 6分
∴MQ=2AQ
即MB+BQ=2AQ
∴CQ+BQ=2AQ …7分
25. (1)①(-3,-1),(2,2)……………………………………………………2分
②(-1,1)……………………………………………………………………...3分
(2)∵点B(1,0)的“正轨点”在直线y=2x+2上,
∴false或false.
∴false或false.……………………………………………………….4分
∴点B的“正轨点”的坐标是false,(-3,-4).………………………...5分
(3)-2<n<2且n≠0…………………….…………………………………..7分
同课章节目录
