2020-2021学年苏科版七年级数学下册课件:8.3幂的除法(27张)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册课件:8.3幂的除法(27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 332.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览



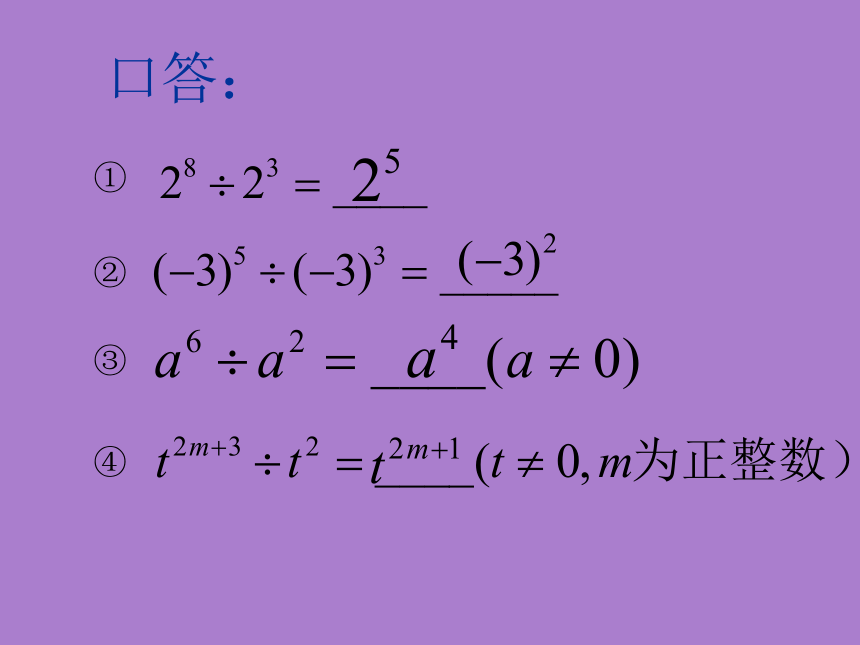

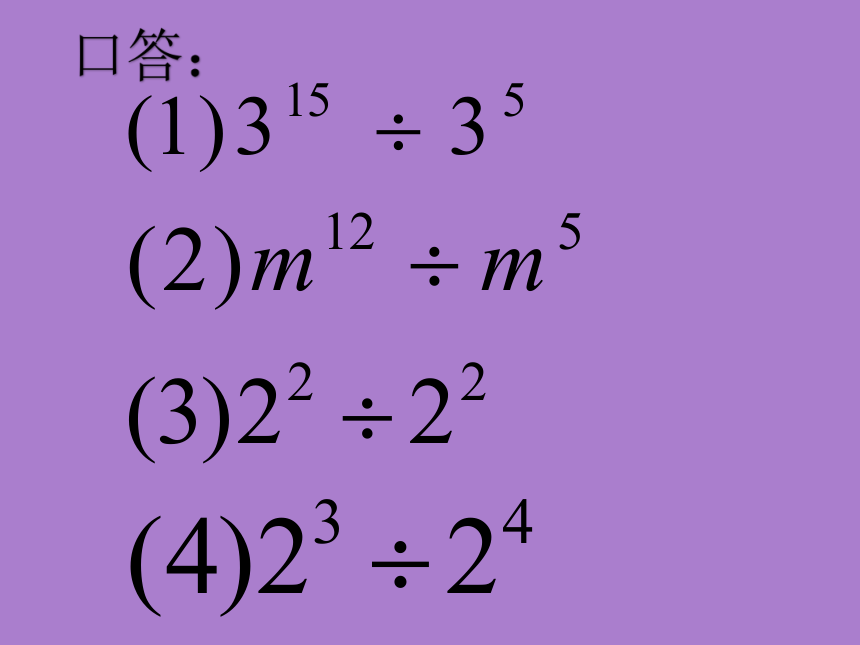

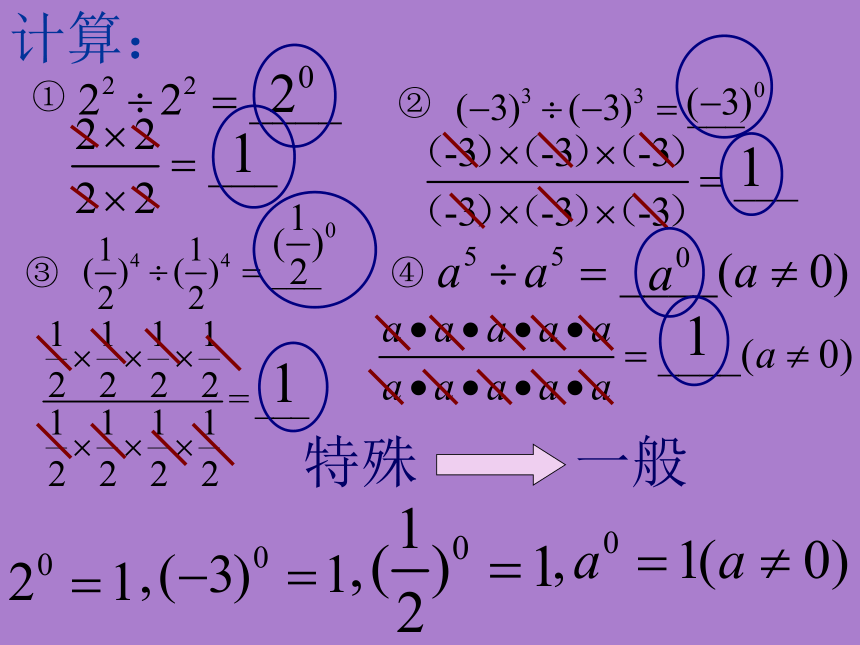

文档简介
2021
8.3 同底数幂的除法(2)
苏科版七年级下册 数学
复习回顾
1
知识回顾
2.am÷an=
1.同底数幂相除,底数____,指数___.
不变
相减
am–n
(a≠0, m、n都是正整数,且m>n)
口答:
①
②
③
④
探索新知
2
口答:
问题1:
当m=n时,结果会怎样呢?
计算:
①
②
③
④
特殊
一般
通过刚才的找规律,我们发现:
实际上,我们知道:
所以:
我们规定:
任何不等于0的数的0次幂等于1。
(0的0次方无意义)
幂的运算性质的适用范围扩展到正整数指数幂和零指数幂。
练一练
问题2:
当m<n时,结果又会怎样呢?
计算:
①
②
③
④
我们规定:
任何不等于0的数的-n次幂,
等于这个数的n次幂的倒数.
(底倒指反)
等于这个数的倒数的n次幂。
综合计算:
①
②
归纳总结:
目前,我们学习的所有幂的相关运算,指数的范围扩大了所有整数。
③
比谁算的快:
②
③
①
底数是分数
④
注意:
幂的运算要看清底数
底数是小数时要转化成分数
转化
练一练
例题讲解
3
例1
用小数或分数表示下列各数:
P57例2
用小数或分数表示下列各数:
(1)4-2;(2)-3-3;(3)3.14×10-4.
=116
?
=?127
?
=0.000314
变式:把下列各数写成负整数指数幂的形式:
(1)164;(2)0.0001;(3)?18.
?
(3)?18=?123=-2-3
?
(2)0.0001=1104=10-4
?
解:(1)164=????????????=8-????
?
例1
用小数或分数表示下列各数
(1) ;(2) ;(3)
解:
(1)
(2)
(3)
1、把下列各数写成负整数指数幂的形式:
①
②
③
④
逆向思维训练:
3、若
,则x= ,
,则
4、
2、若
有意义,则x满足______
例2
把下列各数写成负整指数幂的形式:
填空1
(1) ,则x=_____.
(2)162b=25·211,则b=____.
(4)若0.0000003=3×10m,则
m=________
-5
2
-2
-7
(1)
,则 x= ;
2
x
=
1
8
(2)
,则 x= ;
x
-1
=
1
10
(3)
,则 x= .
10
x
=
0.000 1
-3
10
-4
填空2
课堂小结
4
谈谈本节课收获的知识与方法.
一
二
一
同底数幂除法的运算性质
适用于一切整数指数幂;
个性质:
零指数幂、负指数幂;
个幂:
个方法:
由特殊到一般的思考问题的方法.
五、课堂小结
8.3 同底数幂的除法(2)
苏科版七年级下册 数学
复习回顾
1
知识回顾
2.am÷an=
1.同底数幂相除,底数____,指数___.
不变
相减
am–n
(a≠0, m、n都是正整数,且m>n)
口答:
①
②
③
④
探索新知
2
口答:
问题1:
当m=n时,结果会怎样呢?
计算:
①
②
③
④
特殊
一般
通过刚才的找规律,我们发现:
实际上,我们知道:
所以:
我们规定:
任何不等于0的数的0次幂等于1。
(0的0次方无意义)
幂的运算性质的适用范围扩展到正整数指数幂和零指数幂。
练一练
问题2:
当m<n时,结果又会怎样呢?
计算:
①
②
③
④
我们规定:
任何不等于0的数的-n次幂,
等于这个数的n次幂的倒数.
(底倒指反)
等于这个数的倒数的n次幂。
综合计算:
①
②
归纳总结:
目前,我们学习的所有幂的相关运算,指数的范围扩大了所有整数。
③
比谁算的快:
②
③
①
底数是分数
④
注意:
幂的运算要看清底数
底数是小数时要转化成分数
转化
练一练
例题讲解
3
例1
用小数或分数表示下列各数:
P57例2
用小数或分数表示下列各数:
(1)4-2;(2)-3-3;(3)3.14×10-4.
=116
?
=?127
?
=0.000314
变式:把下列各数写成负整数指数幂的形式:
(1)164;(2)0.0001;(3)?18.
?
(3)?18=?123=-2-3
?
(2)0.0001=1104=10-4
?
解:(1)164=????????????=8-????
?
例1
用小数或分数表示下列各数
(1) ;(2) ;(3)
解:
(1)
(2)
(3)
1、把下列各数写成负整数指数幂的形式:
①
②
③
④
逆向思维训练:
3、若
,则x= ,
,则
4、
2、若
有意义,则x满足______
例2
把下列各数写成负整指数幂的形式:
填空1
(1) ,则x=_____.
(2)162b=25·211,则b=____.
(4)若0.0000003=3×10m,则
m=________
-5
2
-2
-7
(1)
,则 x= ;
2
x
=
1
8
(2)
,则 x= ;
x
-1
=
1
10
(3)
,则 x= .
10
x
=
0.000 1
-3
10
-4
填空2
课堂小结
4
谈谈本节课收获的知识与方法.
一
二
一
同底数幂除法的运算性质
适用于一切整数指数幂;
个性质:
零指数幂、负指数幂;
个幂:
个方法:
由特殊到一般的思考问题的方法.
五、课堂小结
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
