2020--2021学年人教版数学九年级下册26.1反比例函数同步练习试卷(Word版 含解析)
文档属性
| 名称 | 2020--2021学年人教版数学九年级下册26.1反比例函数同步练习试卷(Word版 含解析) | 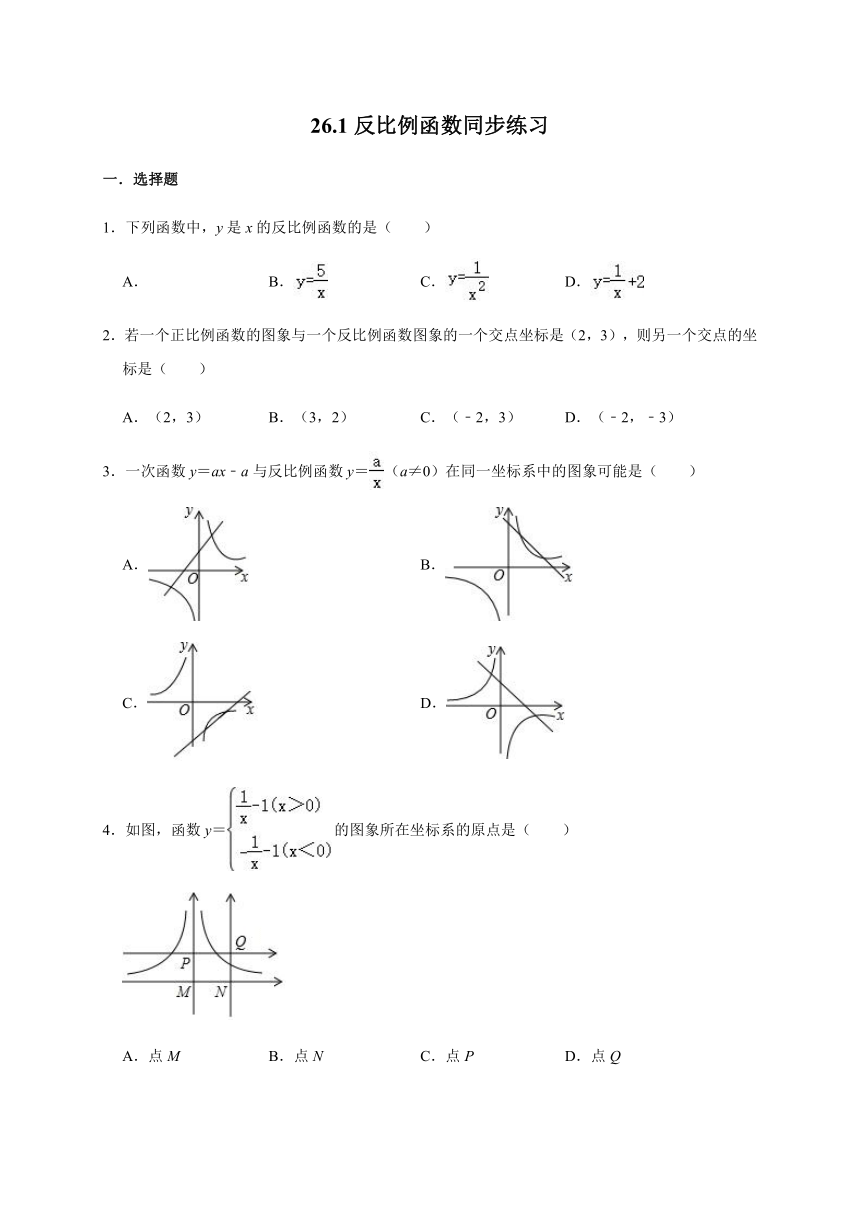 | |
| 格式 | docx | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 12:48:25 | ||
图片预览





文档简介
112268001164590026.1反比例函数同步练习
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A. B. C. D.
2.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,3) D.(﹣2,﹣3)
3.一次函数y=ax﹣a与反比例函数y=(a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
4.如图,函数y=的图象所在坐标系的原点是( )
A.点M B.点N C.点P D.点Q
5.如图,P是双曲线上一点,且图中的阴影部分的面积为3,则此反比例函数的解析式为( )
A.y= B.y=﹣ C.y= D.y=﹣
6.若点A(x1,1)、B(x2,﹣2)、C(x3,﹣3)在反比例函数y=﹣的图象上,则x1、x2、x3的大小关系是( )
A.x1<x2<x3 B.x1<x3<x2 C.x3<x1<x2 D.x2<x1<x3
7.如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数的图象上,若点B(﹣6,0),则反比例函数表达式为( )
A. B. C. D.
8.在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点M(a,b),则代数式的值为( )
A. B.﹣ C. D.﹣
9.如图,已知一次函数y=ax+b与反比例函数y=图象交于M、N两点,则不等式ax+b>解集为( )
A.x>2或﹣1<x<0 B.﹣1<x<0
C.﹣1<x<0或0<x<2 D.x>2
10.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E且四边形OEBF的面积为6,则k的值为( )
A.2 B.4 C.6 D.8
二.填空题
11.如图,Rt△AOB的一条直角边OA在x轴上,且S△AOB=2,若某反比例函数图象的一支经过点B,则该反比例函数的解析式为 .
12.已知反比例函数y=的图象的两个分支在第一、三象限内,那么k的取值范围是 .
13.如图,点M是反比例函数y=(x>0)图象上任意一点,过点M向y轴作垂线,垂足为点N,若点P是x轴上的动点,则△MNP的面积为 .
14.已知函数y=的图象在每个象限内,y的值随x的值增大而减小,则k的取值范围是 .
15.若反比例函数y=,当x≥a或x≤﹣a时,函数值y范围内的整数有k个;当x≥a+1或x≤﹣a﹣1时,函数值y范围内的整数有k﹣2个,则正整数a= .
三.解答题
16.已知一次函数y=kx+b与反比例函数y=的图象交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)请观察图象,直接写出不等式kx+b≤的解集.
17.如图,已知一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(﹣1,2)和点B.
(1)求b和k的值;
(2)请求出点B的坐标,并观察图象,直接写出关于x的不等式x+b>的解集;
(3)若点P在y轴上一点,当PA+PB最小时,求点P的坐标.
18.已知:如图,两点A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b(k≠0)和反比例函数y=(m≠0)图象的两个交点.
(1)求一次函数和反比例函数的的解析式.
(2)求△AOB的面积.
(3)观察图象,直接写出不等式kx+b≥的解集.
19.如图,反比例函数y=上(x>0)过点A(3,4),直线AC与x轴交于C(6,0),过点C作x轴的垂线交反比例函数的图象于点B.
(1)求反比例函数和直线AC的表达式;
(2)求△ABC的面积.
20.如图,直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为8,求△AOC的面积.
(3)若>x>0,直接写出x的取值范围.
参考答案
一.选择题
1.解:A、是正比例函数,不是反比例函数,故此选项不合题意;
B、是反比例函数,故此选项符合题意;
C、不是反比例函数,故此选项不合题意;
D、不是反比例函数,故此选项不合题意;
故选:B.
2.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(2,3)关于原点对称,
∴该点的坐标为(﹣2,﹣3).
故选:D.
3.解:A、由函数y=ax﹣a的图象可知a>0,﹣a>0,由函数y=(a≠0)的图象可知a>0,矛盾,错误;
B、由函数y=ax﹣a的图象可知a<0,由函数y=(a≠0)的图象可知a>0,相矛盾,故错误;
C、由函数y=ax﹣a的图象可知a>0,由函数y=(a≠0)的图象可知a<0,故错误;
D、由函数y=ax﹣a的图象可知a<0,﹣a>0,由函数y=(a≠0)的图象可知a<0,故正确;
故选:D.
4.解:由函数解析式和图象可知函数y=关于y轴对称,且在y=﹣1的上面,
所以点P是原点.
故选:C.
5.解:由题意得:点P是反比例函数图象上一点,S==3.
又由于反比例函数图象位于二、四象限,k<0,
则k=﹣6,故反比例函数的解析式为y=﹣.
故选:B.
6.解:∵反比例函数为y=y=﹣中的﹣(k2+1)<0,
∴函数图象在第二、四象限,在每个象限内,y随着x的增大而增大,
又∵A(x1,1)、B(x2,﹣2)、C(x3,﹣3)
∴x1<0,点B、C位于第四象限,
∴x2>x3>0.
∴x1<x3<x2
故选:B.
7.解:过点C作CD⊥x轴于D,
∵点B(﹣6,0),
∴菱形的边长为6,
∵在菱形ABOC中,∠A=60°,
∴∠DOC=60°,
在Rt△CDO中,OD=6×cos60°=3,CD=6×sin60°=3,
则C(﹣3,3),
∵顶点C在反比例函数的图象上,
∴k=﹣3×=﹣9,
∴反比例函数为y=﹣,
故选:D.
8.解:∵函数y=(x>0)与y=x﹣1的图象交于点M(a,b),
∴ab=4,b=a﹣1,
∴b﹣a=﹣1,
∴===﹣;
故选:D.
9.解:由图可知,x>2或﹣1<x<0时,ax+b>.
故选:A.
10.解:设F(a,),则B(a,),
因为矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF,
所以k+k+6=a?,
解得k=6,
故选:C.
二.填空题
11.解:设反比例函数的关系式为y=,
由题意得,S△AOB=2=|k|,
所以k=﹣4或k=4(舍去),
反比例函数的关系式为y=﹣,
故答案为:y=﹣.
12.解:∵反比例函数y=的图象的两个分支在第一、三象限内,
∴3k﹣2>0,
解得:k>,
故答案为k>.
13.解:设M的坐标是(m,n),则mn=4.
∵MN=m,△MNP的MN边上的高等于n.
∴△MNP的面积=mn=2.
故答案为2.
14.解:由题意可知:k﹣5>0,
∴k>5,
故答案为:k>5.
15.解:根据题意,反比例函数y=中,
当x≥a或x≤﹣a时,则﹣≤y≤,且y≠0,
同理,x≥a+1或x≤﹣a﹣1时,则﹣≤y≤,且y≠0,
∴正整数a只能为1、2、3、4,
∴当a=1时,
∵﹣≤y≤,
∴﹣4≤y≤4,且y≠0,则k=8;
∵﹣≤y≤,
∴﹣2≤y≤2,且y≠0,则k=4;
∴a=1不合题意;
同理可求,
当a=2时,符合题意;
当a=3时,不合题意;
当a=4时,符合题意;
综上,正整数a为2或4,
故答案为2或4.
三.解答题
16.解:(1)∵反比例函数y=的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,解得,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y=﹣;
(2)如图设直线AB交y轴于C,则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB=×4×3+×4×1=8;
(3)观察函数图象知,不等式kx+b≤的解集为﹣3≤x<0或x≥1.
17.解:(1)∵一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(﹣1,2),
把A(﹣1,2)代入两个解析式得:2=×(﹣1)+b,2=﹣k,
解得:b=,k=﹣2;
(2)联立一次函数解析式与反比例函数解析式成方程组:,
解得:或,
∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4,).
观察函数图象可知:关于x的不等式x+b>的解集x为﹣4<x<﹣1或x>0.
(3)作点A关于y轴的对称点A′,连接A′B交y轴于点P,此时点P即是所求,如图所示.
∵点A′与点A关于y轴对称,
∴点A′的坐标为(1,2),
设直线A′B的解析式为y=mx+n,
∴,解得:,
∴直线A′B的解析式为y=x+.
令x=0,则y=,
∴点P的坐标为(0,).
18.解:(1)∵A(﹣4,2)在上,
∴m=﹣4×2=﹣8.
∴反比例函数的解析式为.
∵B(n,﹣4)在上,
∴n=2,
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴,
解之得,
∴一次函数的解析式为y=﹣x﹣2;
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO==6;
(3)由图可得,不等式kx+b≥的解集为x≤﹣4或0<x≤2.
19.解:(1)把(3,4)代入反比例函数y=上,
得到k=12,所以反比例函数解析式为y=;
设直线AC的解析式为y=kx+b,代入(3,4)和(6,0),得
,解得,
所以y=﹣x+8;
(2)过A点作AH垂直于CB延长线于H点,
则AH=6﹣3=3.
由题意可知B点的横坐标为6,把x=6代入y=中,可得y=2,
所以B点坐标为(6,2).
则CB=2.
△ABC的面积为BC×AH=×2×3=3.
20.解:(1)∵点A的横坐标为4,点A在直线y=x上,
∴点A的纵坐标为y=×4=2,即A(4,2).
又∵点A(4,2)在双曲线y=上,
∴k=2×4=8;
(2)∵点C在双曲线y=上,且点C纵坐标为8,
∴C(1,8).
如图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.
∵S△COM=S△AON==4,
∴S△AOC=S四边形CMNA=×(|yA|+|yC|)×(|xA|﹣|xc|)=15.
(3)若>x>0,则x的取值范围是0<x<4.
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A. B. C. D.
2.若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2,3),则另一个交点的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,3) D.(﹣2,﹣3)
3.一次函数y=ax﹣a与反比例函数y=(a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
4.如图,函数y=的图象所在坐标系的原点是( )
A.点M B.点N C.点P D.点Q
5.如图,P是双曲线上一点,且图中的阴影部分的面积为3,则此反比例函数的解析式为( )
A.y= B.y=﹣ C.y= D.y=﹣
6.若点A(x1,1)、B(x2,﹣2)、C(x3,﹣3)在反比例函数y=﹣的图象上,则x1、x2、x3的大小关系是( )
A.x1<x2<x3 B.x1<x3<x2 C.x3<x1<x2 D.x2<x1<x3
7.如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数的图象上,若点B(﹣6,0),则反比例函数表达式为( )
A. B. C. D.
8.在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点M(a,b),则代数式的值为( )
A. B.﹣ C. D.﹣
9.如图,已知一次函数y=ax+b与反比例函数y=图象交于M、N两点,则不等式ax+b>解集为( )
A.x>2或﹣1<x<0 B.﹣1<x<0
C.﹣1<x<0或0<x<2 D.x>2
10.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E且四边形OEBF的面积为6,则k的值为( )
A.2 B.4 C.6 D.8
二.填空题
11.如图,Rt△AOB的一条直角边OA在x轴上,且S△AOB=2,若某反比例函数图象的一支经过点B,则该反比例函数的解析式为 .
12.已知反比例函数y=的图象的两个分支在第一、三象限内,那么k的取值范围是 .
13.如图,点M是反比例函数y=(x>0)图象上任意一点,过点M向y轴作垂线,垂足为点N,若点P是x轴上的动点,则△MNP的面积为 .
14.已知函数y=的图象在每个象限内,y的值随x的值增大而减小,则k的取值范围是 .
15.若反比例函数y=,当x≥a或x≤﹣a时,函数值y范围内的整数有k个;当x≥a+1或x≤﹣a﹣1时,函数值y范围内的整数有k﹣2个,则正整数a= .
三.解答题
16.已知一次函数y=kx+b与反比例函数y=的图象交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)请观察图象,直接写出不等式kx+b≤的解集.
17.如图,已知一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(﹣1,2)和点B.
(1)求b和k的值;
(2)请求出点B的坐标,并观察图象,直接写出关于x的不等式x+b>的解集;
(3)若点P在y轴上一点,当PA+PB最小时,求点P的坐标.
18.已知:如图,两点A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b(k≠0)和反比例函数y=(m≠0)图象的两个交点.
(1)求一次函数和反比例函数的的解析式.
(2)求△AOB的面积.
(3)观察图象,直接写出不等式kx+b≥的解集.
19.如图,反比例函数y=上(x>0)过点A(3,4),直线AC与x轴交于C(6,0),过点C作x轴的垂线交反比例函数的图象于点B.
(1)求反比例函数和直线AC的表达式;
(2)求△ABC的面积.
20.如图,直线y=x与双曲线y=(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=(k>0)上一点C的纵坐标为8,求△AOC的面积.
(3)若>x>0,直接写出x的取值范围.
参考答案
一.选择题
1.解:A、是正比例函数,不是反比例函数,故此选项不合题意;
B、是反比例函数,故此选项符合题意;
C、不是反比例函数,故此选项不合题意;
D、不是反比例函数,故此选项不合题意;
故选:B.
2.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(2,3)关于原点对称,
∴该点的坐标为(﹣2,﹣3).
故选:D.
3.解:A、由函数y=ax﹣a的图象可知a>0,﹣a>0,由函数y=(a≠0)的图象可知a>0,矛盾,错误;
B、由函数y=ax﹣a的图象可知a<0,由函数y=(a≠0)的图象可知a>0,相矛盾,故错误;
C、由函数y=ax﹣a的图象可知a>0,由函数y=(a≠0)的图象可知a<0,故错误;
D、由函数y=ax﹣a的图象可知a<0,﹣a>0,由函数y=(a≠0)的图象可知a<0,故正确;
故选:D.
4.解:由函数解析式和图象可知函数y=关于y轴对称,且在y=﹣1的上面,
所以点P是原点.
故选:C.
5.解:由题意得:点P是反比例函数图象上一点,S==3.
又由于反比例函数图象位于二、四象限,k<0,
则k=﹣6,故反比例函数的解析式为y=﹣.
故选:B.
6.解:∵反比例函数为y=y=﹣中的﹣(k2+1)<0,
∴函数图象在第二、四象限,在每个象限内,y随着x的增大而增大,
又∵A(x1,1)、B(x2,﹣2)、C(x3,﹣3)
∴x1<0,点B、C位于第四象限,
∴x2>x3>0.
∴x1<x3<x2
故选:B.
7.解:过点C作CD⊥x轴于D,
∵点B(﹣6,0),
∴菱形的边长为6,
∵在菱形ABOC中,∠A=60°,
∴∠DOC=60°,
在Rt△CDO中,OD=6×cos60°=3,CD=6×sin60°=3,
则C(﹣3,3),
∵顶点C在反比例函数的图象上,
∴k=﹣3×=﹣9,
∴反比例函数为y=﹣,
故选:D.
8.解:∵函数y=(x>0)与y=x﹣1的图象交于点M(a,b),
∴ab=4,b=a﹣1,
∴b﹣a=﹣1,
∴===﹣;
故选:D.
9.解:由图可知,x>2或﹣1<x<0时,ax+b>.
故选:A.
10.解:设F(a,),则B(a,),
因为矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF,
所以k+k+6=a?,
解得k=6,
故选:C.
二.填空题
11.解:设反比例函数的关系式为y=,
由题意得,S△AOB=2=|k|,
所以k=﹣4或k=4(舍去),
反比例函数的关系式为y=﹣,
故答案为:y=﹣.
12.解:∵反比例函数y=的图象的两个分支在第一、三象限内,
∴3k﹣2>0,
解得:k>,
故答案为k>.
13.解:设M的坐标是(m,n),则mn=4.
∵MN=m,△MNP的MN边上的高等于n.
∴△MNP的面积=mn=2.
故答案为2.
14.解:由题意可知:k﹣5>0,
∴k>5,
故答案为:k>5.
15.解:根据题意,反比例函数y=中,
当x≥a或x≤﹣a时,则﹣≤y≤,且y≠0,
同理,x≥a+1或x≤﹣a﹣1时,则﹣≤y≤,且y≠0,
∴正整数a只能为1、2、3、4,
∴当a=1时,
∵﹣≤y≤,
∴﹣4≤y≤4,且y≠0,则k=8;
∵﹣≤y≤,
∴﹣2≤y≤2,且y≠0,则k=4;
∴a=1不合题意;
同理可求,
当a=2时,符合题意;
当a=3时,不合题意;
当a=4时,符合题意;
综上,正整数a为2或4,
故答案为2或4.
三.解答题
16.解:(1)∵反比例函数y=的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,解得,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y=﹣;
(2)如图设直线AB交y轴于C,则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB=×4×3+×4×1=8;
(3)观察函数图象知,不等式kx+b≤的解集为﹣3≤x<0或x≥1.
17.解:(1)∵一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(﹣1,2),
把A(﹣1,2)代入两个解析式得:2=×(﹣1)+b,2=﹣k,
解得:b=,k=﹣2;
(2)联立一次函数解析式与反比例函数解析式成方程组:,
解得:或,
∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4,).
观察函数图象可知:关于x的不等式x+b>的解集x为﹣4<x<﹣1或x>0.
(3)作点A关于y轴的对称点A′,连接A′B交y轴于点P,此时点P即是所求,如图所示.
∵点A′与点A关于y轴对称,
∴点A′的坐标为(1,2),
设直线A′B的解析式为y=mx+n,
∴,解得:,
∴直线A′B的解析式为y=x+.
令x=0,则y=,
∴点P的坐标为(0,).
18.解:(1)∵A(﹣4,2)在上,
∴m=﹣4×2=﹣8.
∴反比例函数的解析式为.
∵B(n,﹣4)在上,
∴n=2,
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴,
解之得,
∴一次函数的解析式为y=﹣x﹣2;
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=﹣2.
∴点C(﹣2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO==6;
(3)由图可得,不等式kx+b≥的解集为x≤﹣4或0<x≤2.
19.解:(1)把(3,4)代入反比例函数y=上,
得到k=12,所以反比例函数解析式为y=;
设直线AC的解析式为y=kx+b,代入(3,4)和(6,0),得
,解得,
所以y=﹣x+8;
(2)过A点作AH垂直于CB延长线于H点,
则AH=6﹣3=3.
由题意可知B点的横坐标为6,把x=6代入y=中,可得y=2,
所以B点坐标为(6,2).
则CB=2.
△ABC的面积为BC×AH=×2×3=3.
20.解:(1)∵点A的横坐标为4,点A在直线y=x上,
∴点A的纵坐标为y=×4=2,即A(4,2).
又∵点A(4,2)在双曲线y=上,
∴k=2×4=8;
(2)∵点C在双曲线y=上,且点C纵坐标为8,
∴C(1,8).
如图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.
∵S△COM=S△AON==4,
∴S△AOC=S四边形CMNA=×(|yA|+|yC|)×(|xA|﹣|xc|)=15.
(3)若>x>0,则x的取值范围是0<x<4.
