17.1 勾股定理(第3课时) 课件(共20张PPT)
文档属性
| 名称 | 17.1 勾股定理(第3课时) 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 14:32:52 | ||
图片预览








文档简介
(共20张PPT)
人教版
八年级下
17.1
勾股定理(三)
新知导入
1.请叙述勾股定理的内容.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△
ABC中,∠C=90°,
那么
a
b
c
A
B
C
小试牛刀
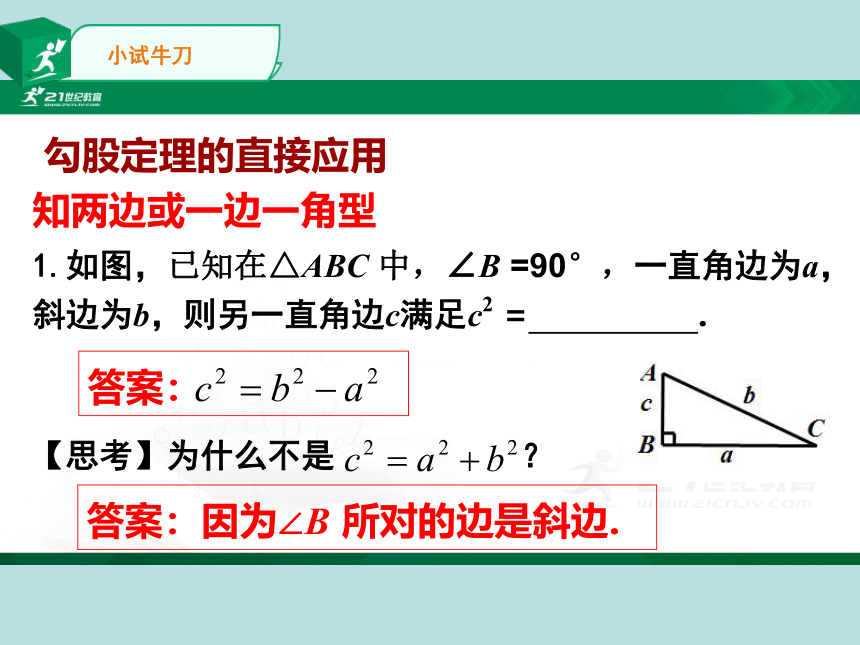
1.如图,已知在△ABC
中,∠B
=90°,一直角边为a,斜边为b,则另一直角边c满足c2
=
.
【思考】为什么不是
?
勾股定理的直接应用
知两边或一边一角型
答案:因为∠B
所对的边是斜边.
答案:
在△ABC中,∠C
=
90°,
AB
=
8
C
A
B
解:
(1)若∠A
=
45°,求
BC
、
CA
的长度;
45°
8
在Rt△ABC中,根据勾股定理
(2)若∠A
=
30°,求
BC的长为
;
CA
的长为
;
C
A
B
30°
8
4
新知探索
数学海螺图:
在数学中也有这样一幅美丽的“海螺型”图案
新知探索
由此可知,利用勾股定理,可以作出长为
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
你能在数轴上表示出
的点吗?
的线段.
新知探索
你能在数轴上表示出
的点吗?
-1
0
1
2
3
你能在数轴上画出表示
的点吗?
探究1:
√
√
新知探索
新知探索
利用勾股定理,长为
的线段是直角边为正整数
和
的三角形的斜边;
如何在数轴上表示无理数:
C
A
B
3
2
-1
0
1
2
3
4
5
新知讲解
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点。
你能在数轴上画出表示
的点
和
的点吗?
∴点C即为表示
的点
新知讲解
方法总结:
在数轴上表示无理数的点,关键是构造
直角三角形,使直角三角形斜边等于所要表示的无理数,这一步常借助于勾股定理来完成。
问题解决
你能在数轴上画出表示
的点和
的点吗?
√
A
C
B
l
0
1
2
3
4
0
1
2
3
4
5
A
课堂练习
1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为
的线段?
A
课堂练习
2.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
1.在数轴上画出无理数;
2.会用勾股定理解决简单的实际问题。
作业:
1.必做题:习题17.1
第6,
8,9题。
2.选做题:
课本习题17.1
第14题。
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版
八年级下
17.1
勾股定理(三)
新知导入
1.请叙述勾股定理的内容.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△
ABC中,∠C=90°,
那么
a
b
c
A
B
C
小试牛刀
1.如图,已知在△ABC
中,∠B
=90°,一直角边为a,斜边为b,则另一直角边c满足c2
=
.
【思考】为什么不是
?
勾股定理的直接应用
知两边或一边一角型
答案:因为∠B
所对的边是斜边.
答案:
在△ABC中,∠C
=
90°,
AB
=
8
C
A
B
解:
(1)若∠A
=
45°,求
BC
、
CA
的长度;
45°
8
在Rt△ABC中,根据勾股定理
(2)若∠A
=
30°,求
BC的长为
;
CA
的长为
;
C
A
B
30°
8
4
新知探索
数学海螺图:
在数学中也有这样一幅美丽的“海螺型”图案
新知探索
由此可知,利用勾股定理,可以作出长为
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
你能在数轴上表示出
的点吗?
的线段.
新知探索
你能在数轴上表示出
的点吗?
-1
0
1
2
3
你能在数轴上画出表示
的点吗?
探究1:
√
√
新知探索
新知探索
利用勾股定理,长为
的线段是直角边为正整数
和
的三角形的斜边;
如何在数轴上表示无理数:
C
A
B
3
2
-1
0
1
2
3
4
5
新知讲解
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点。
你能在数轴上画出表示
的点
和
的点吗?
∴点C即为表示
的点
新知讲解
方法总结:
在数轴上表示无理数的点,关键是构造
直角三角形,使直角三角形斜边等于所要表示的无理数,这一步常借助于勾股定理来完成。
问题解决
你能在数轴上画出表示
的点和
的点吗?
√
A
C
B
l
0
1
2
3
4
0
1
2
3
4
5
A
课堂练习
1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为
的线段?
A
课堂练习
2.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
1.在数轴上画出无理数;
2.会用勾股定理解决简单的实际问题。
作业:
1.必做题:习题17.1
第6,
8,9题。
2.选做题:
课本习题17.1
第14题。
课堂小结
https://www.21cnjy.com/help/help_extract.php
