24.6 正多边形与圆同步课时训练(含答案)
文档属性
| 名称 | 24.6 正多边形与圆同步课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 487.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览




文档简介
24.6正多边形与圆课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2false B.2 C.false D.4
2.已知正六边形false内接于false,若false的直径为false,则该正六边形的周长是( )
A.false B.false C.false D.false
3.如图,false,false分别为false的内接正三角形和内接正四边形的一边,若false恰好是同圆的一个内接正false边形的一边,则false的值为( )
A.8 B.10 C.12 D.14
4.如图,正五边形false内接于false,点false为false上一点(点false与点false,点false不重合),连接false,false,false,垂足为false,则false等于( )
A.72° B.54° C.36° D.64°
5.一个圆的内接正六边形与内接正方形的边长之比为( )
A.false B.false C.false D.false
6.如图,正六边形false内接于false,连接false,则false的度数是( )
A.false B.false C.false D.false
7.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶false B.false∶false C.3∶2 D.1∶2
8.如图,⊙O是正六边形ABCDEF的外接圆,⊙O的半径长为a,下列说法中不正确的是( )
A.正六边形ABCDEF的中心角等于60° B.正六边形ABCDEF的周长等于6a
C.正六边形ABCDEF的边心距等于false D.正六边形ABCDEF的面积等于3false
9.如图,正false内接于半径是1的圆,则阴影部分的面积是( )
A.false B.false C.false D.false
10.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8 B.10 C.12 D.15
二、填空题
11.一个半径为4cm的圆内接正六边形的周长等于_____cm.
12.如图,已知false为false直径,若false是false内接正false边形的一边,false是false内接正false边形的一边,false,则false_____.
13.公元263年左右,我国数学家刘徽发现当正多边形的边数无限增加时,这个正多边形面积可无限接近它的外接圆的面积,因此可以用正多边形的面积来近似估计圆的面积,如图,false是正十二边形的外接圆,设正十二边形的半径false的长为1,如果用它的面积来近似估计false的面积,那么false的面积约是___.
14.如图,正五边形false内接于false,false是false的中点,则false的度数为________.
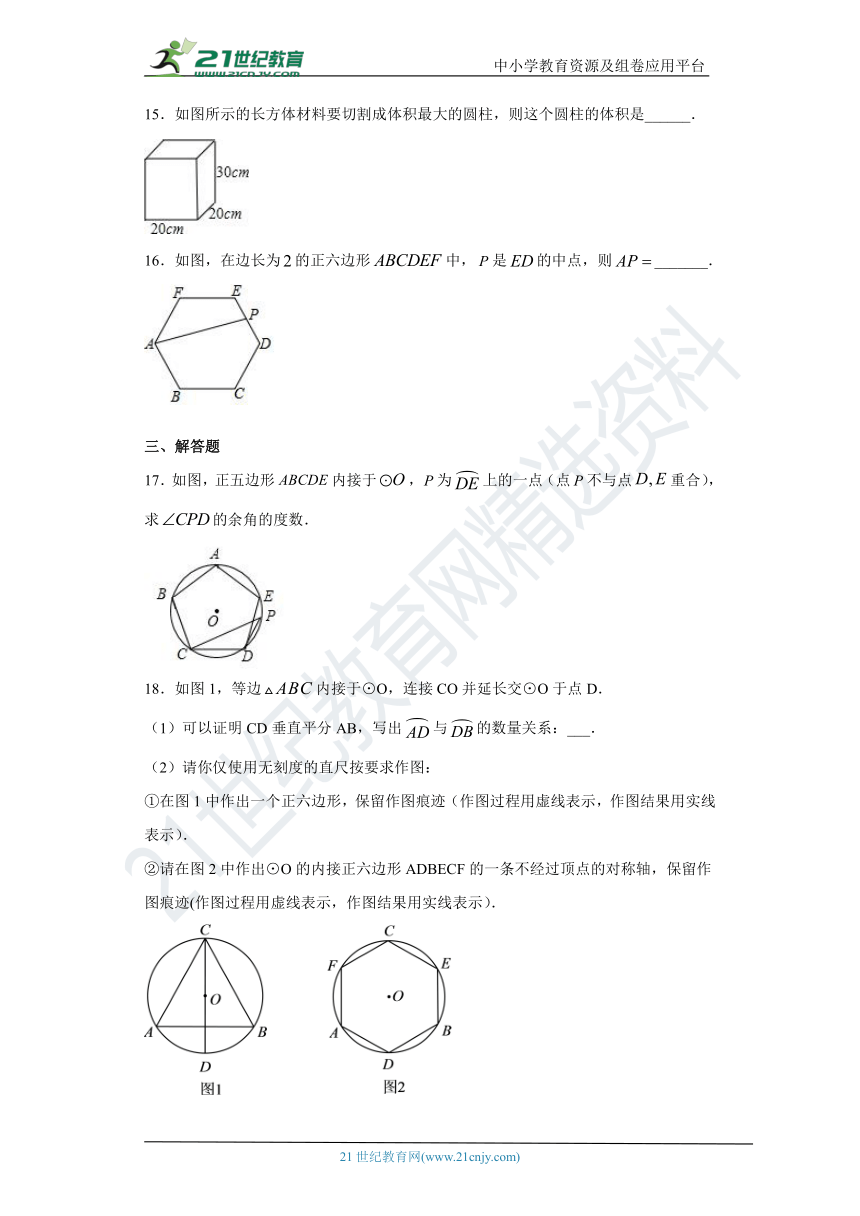
15.如图所示的长方体材料要切割成体积最大的圆柱,则这个圆柱的体积是______.
16.如图,在边长为false的正六边形false中,false是false的中点,则false_______.
三、解答题
17.如图,正五边形false内接于false,false为false上的一点(点false不与点false重合),求false的余角的度数.
18.如图1,等边false内接于⊙O,连接CO并延长交⊙O于点D.
(1)可以证明CD垂直平分AB,写出false与false的数量关系:___.
(2)请你仅使用无刻度的直尺按要求作图:
①在图1中作出一个正六边形,保留作图痕迹(作图过程用虚线表示,作图结果用实线表示).
②请在图2中作出⊙O的内接正六边形ADBECF的一条不经过顶点的对称轴,保留作图痕迹(作图过程用虚线表示,作图结果用实线表示).
19.如图,false的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若false,false且false,请你用含有false、false的代数式表示∠A的度数.
20.如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
(1)求证:BF=DE;
(2)若DE=2,AE=6,DF=12.求⊙O的直径.
参考答案
1.A
2.C
3.C
4.B
5.C
6.D
7.B
8.D
9.A
10.C
11.24
12.false
13.false
14.false
15.falsecm3
16.false
17.54°
解:
如图,连接false.
∵五边形false是正五边形,
∴false,
∴false,
∴90°-36°=54°,
∴false的余角的度数为54°.
18.(1)false;(2)①见解析,②见解析
解:(1)false,
∵O为三角形的外心,
∴O为三角形三边中垂线的交点,
又∵三角形为等边三角形,
∴可得CD垂直平分AB,
根据垂径定理可得:false;
(2)①如图所示,在(1)的基础之上,连接AO,并延长至E,连接BO,并延长至F,顺次连接圆周上各点即可;
②如图所示:(方法不唯一)
19.(1)∠A=48°;(2)∠A=90°false.
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又false,false
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+false,
∵∠A+∠BCD=180°,
∴∠A=90°-false;
20.(1)证明见解析;(2)圆的直径为10false.
解:(1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,
∵OM⊥BD,
∴BM=DM,
∵AC为直径,
∴∠AHC=90°,
∵AE⊥BD于E,CF⊥BD,
∴四边形AHFE为矩形,MN∥AE∥FH,
∵ON∥CH,点O为AC的中点,
∴点N为AH的中点,
∴M点为EF的中点,
∴FM=EM,
∴BM﹣FM=DM﹣EM,
即BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,
∵DE=2,DF=12,
∴BF=2,EF=12﹣2=10,BE=12,
∴AH=EF=10,
在Rt△ADE中,ADfalse2false,
在Rt△ABE中,ABfalse6false,
∵AC为直径,
∴∠ABC=90°,
∵∠ACB=∠ADE,
∴Rt△ACB∽Rt△ADE,
∴false,即false,
解得:AC=10false,
即圆的直径为10false.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2false B.2 C.false D.4
2.已知正六边形false内接于false,若false的直径为false,则该正六边形的周长是( )
A.false B.false C.false D.false
3.如图,false,false分别为false的内接正三角形和内接正四边形的一边,若false恰好是同圆的一个内接正false边形的一边,则false的值为( )
A.8 B.10 C.12 D.14
4.如图,正五边形false内接于false,点false为false上一点(点false与点false,点false不重合),连接false,false,false,垂足为false,则false等于( )
A.72° B.54° C.36° D.64°
5.一个圆的内接正六边形与内接正方形的边长之比为( )
A.false B.false C.false D.false
6.如图,正六边形false内接于false,连接false,则false的度数是( )
A.false B.false C.false D.false
7.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶false B.false∶false C.3∶2 D.1∶2
8.如图,⊙O是正六边形ABCDEF的外接圆,⊙O的半径长为a,下列说法中不正确的是( )
A.正六边形ABCDEF的中心角等于60° B.正六边形ABCDEF的周长等于6a
C.正六边形ABCDEF的边心距等于false D.正六边形ABCDEF的面积等于3false
9.如图,正false内接于半径是1的圆,则阴影部分的面积是( )
A.false B.false C.false D.false
10.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8 B.10 C.12 D.15
二、填空题
11.一个半径为4cm的圆内接正六边形的周长等于_____cm.
12.如图,已知false为false直径,若false是false内接正false边形的一边,false是false内接正false边形的一边,false,则false_____.
13.公元263年左右,我国数学家刘徽发现当正多边形的边数无限增加时,这个正多边形面积可无限接近它的外接圆的面积,因此可以用正多边形的面积来近似估计圆的面积,如图,false是正十二边形的外接圆,设正十二边形的半径false的长为1,如果用它的面积来近似估计false的面积,那么false的面积约是___.
14.如图,正五边形false内接于false,false是false的中点,则false的度数为________.
15.如图所示的长方体材料要切割成体积最大的圆柱,则这个圆柱的体积是______.
16.如图,在边长为false的正六边形false中,false是false的中点,则false_______.
三、解答题
17.如图,正五边形false内接于false,false为false上的一点(点false不与点false重合),求false的余角的度数.
18.如图1,等边false内接于⊙O,连接CO并延长交⊙O于点D.
(1)可以证明CD垂直平分AB,写出false与false的数量关系:___.
(2)请你仅使用无刻度的直尺按要求作图:
①在图1中作出一个正六边形,保留作图痕迹(作图过程用虚线表示,作图结果用实线表示).
②请在图2中作出⊙O的内接正六边形ADBECF的一条不经过顶点的对称轴,保留作图痕迹(作图过程用虚线表示,作图结果用实线表示).
19.如图,false的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若false,false且false,请你用含有false、false的代数式表示∠A的度数.
20.如图,四边形ABCD为⊙O的内接四边形,AC为⊙O直径,AE⊥BD于E,CF⊥BD于F.
(1)求证:BF=DE;
(2)若DE=2,AE=6,DF=12.求⊙O的直径.
参考答案
1.A
2.C
3.C
4.B
5.C
6.D
7.B
8.D
9.A
10.C
11.24
12.false
13.false
14.false
15.falsecm3
16.false
17.54°
解:
如图,连接false.
∵五边形false是正五边形,
∴false,
∴false,
∴90°-36°=54°,
∴false的余角的度数为54°.
18.(1)false;(2)①见解析,②见解析
解:(1)false,
∵O为三角形的外心,
∴O为三角形三边中垂线的交点,
又∵三角形为等边三角形,
∴可得CD垂直平分AB,
根据垂径定理可得:false;
(2)①如图所示,在(1)的基础之上,连接AO,并延长至E,连接BO,并延长至F,顺次连接圆周上各点即可;
②如图所示:(方法不唯一)
19.(1)∠A=48°;(2)∠A=90°false.
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又false,false
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+false,
∵∠A+∠BCD=180°,
∴∠A=90°-false;
20.(1)证明见解析;(2)圆的直径为10false.
解:(1)证明:延长CF交⊙O于H,连接AH,作OM⊥BD于M,延长MO交AH于N,如图,
∵OM⊥BD,
∴BM=DM,
∵AC为直径,
∴∠AHC=90°,
∵AE⊥BD于E,CF⊥BD,
∴四边形AHFE为矩形,MN∥AE∥FH,
∵ON∥CH,点O为AC的中点,
∴点N为AH的中点,
∴M点为EF的中点,
∴FM=EM,
∴BM﹣FM=DM﹣EM,
即BF=DE;
(2)解:易得四边形ANME为矩形,则MN=AE=6,
∵DE=2,DF=12,
∴BF=2,EF=12﹣2=10,BE=12,
∴AH=EF=10,
在Rt△ADE中,ADfalse2false,
在Rt△ABE中,ABfalse6false,
∵AC为直径,
∴∠ABC=90°,
∵∠ACB=∠ADE,
∴Rt△ACB∽Rt△ADE,
∴false,即false,
解得:AC=10false,
即圆的直径为10false.
