六年级数学下册试题 一课一练《圆柱和圆锥》习题3-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《圆柱和圆锥》习题3-北师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 334.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览


文档简介
《圆柱和圆锥》习题3
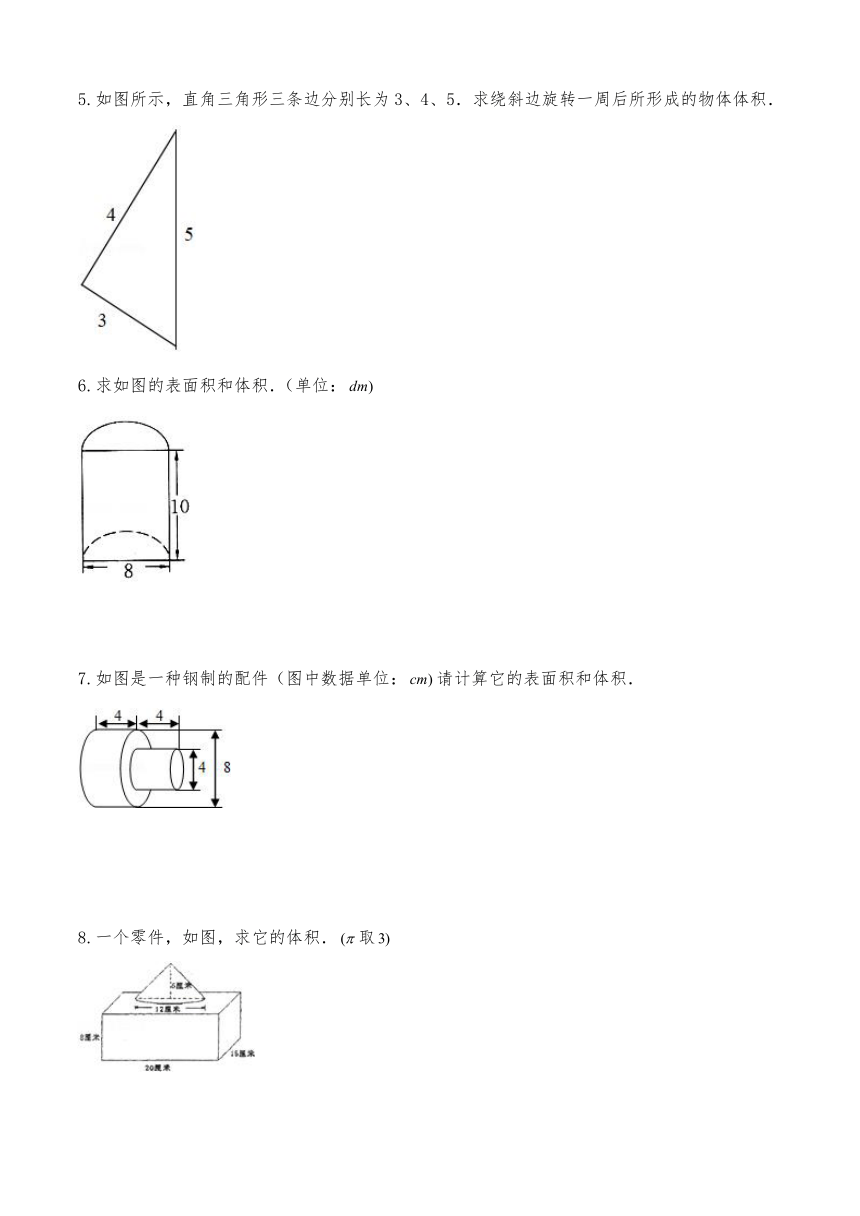
1.学校准备做12个无盖的圆柱体垃圾桶,底面直径为6分米,高8分米,至少需要铁皮多少平方米?(得数保留一位小数)
2.如图是在圆柱里挖去一个圆锥,求它的体积(单位:厘米)
3.一个粮囤如图所示,上面是圆锥形,下面是圆柱形.如果每立方米粮食重800千克.这个粮囤一共可以装多少吨粮食?
4.计算下面立体图形的体积(单位:
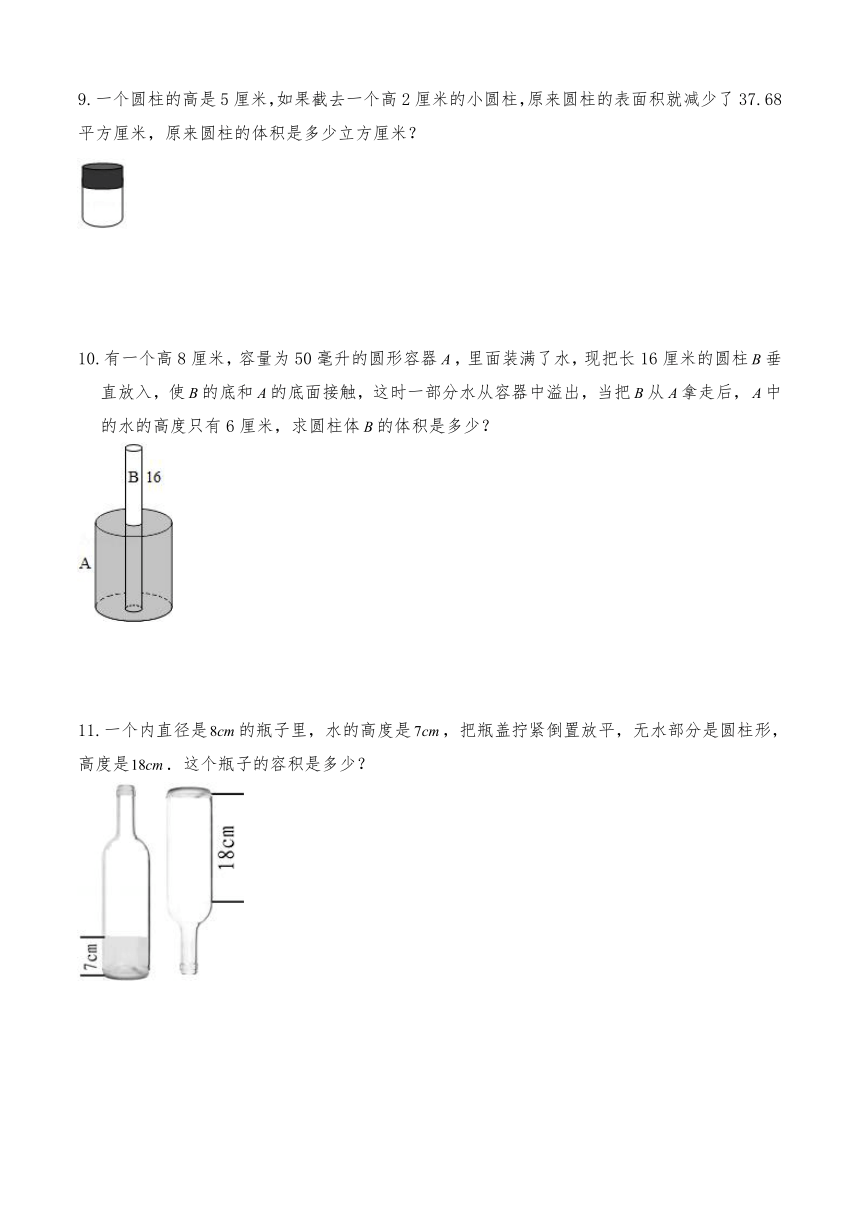
5.如图所示,直角三角形三条边分别长为3、4、5.求绕斜边旋转一周后所形成的物体体积.
6.求如图的表面积和体积.(单位:
7.如图是一种钢制的配件(图中数据单位:请计算它的表面积和体积.
8.一个零件,如图,求它的体积.取
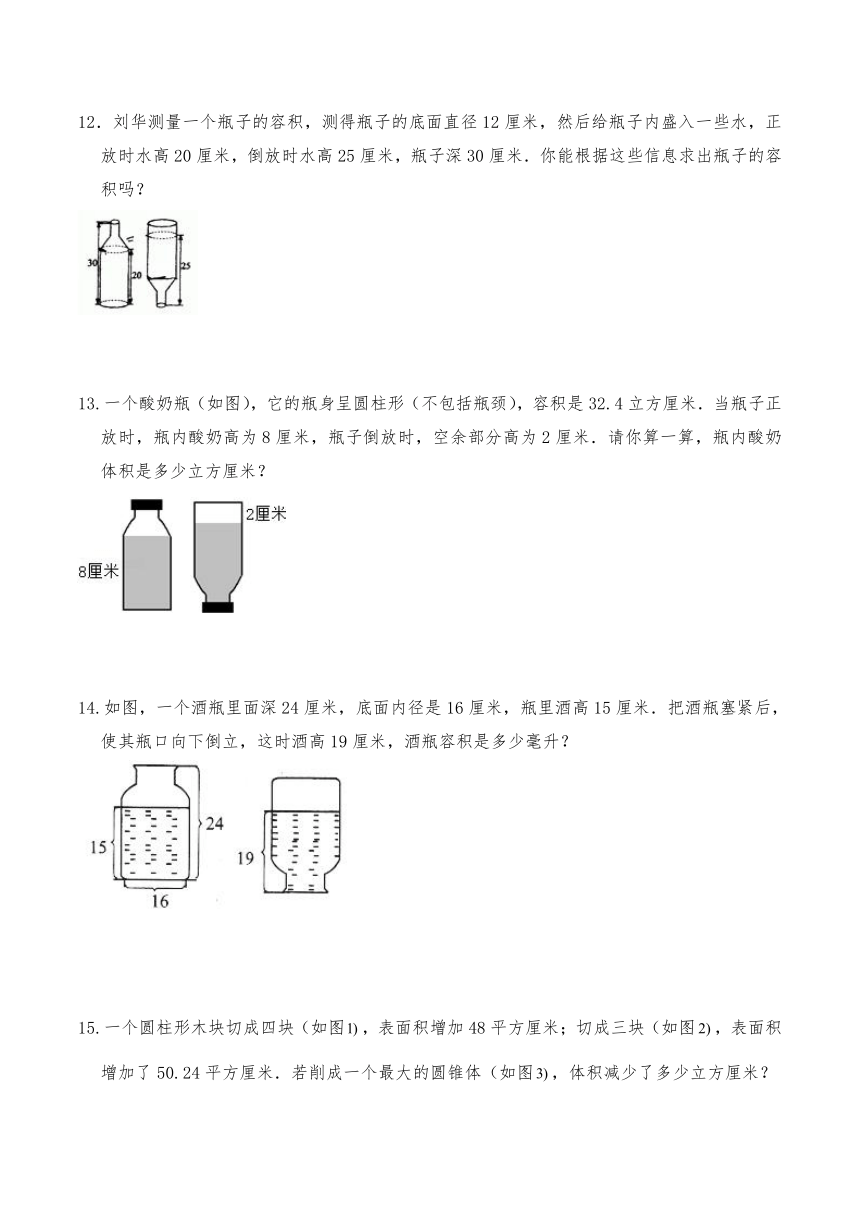
9.一个圆柱的高是5厘米,如果截去一个高2厘米的小圆柱,原来圆柱的表面积就减少了37.68平方厘米,原来圆柱的体积是多少立方厘米?
10.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
11.一个内直径是的瓶子里,水的高度是,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是.这个瓶子的容积是多少?
12.刘华测量一个瓶子的容积,测得瓶子的底面直径12厘米,然后给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,瓶子深30厘米.你能根据这些信息求出瓶子的容积吗?
13.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
14.如图,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒高15厘米.把酒瓶塞紧后,使其瓶口向下倒立,这时酒高19厘米,酒瓶容积是多少毫升?
15.一个圆柱形木块切成四块(如图,表面积增加48平方厘米;切成三块(如图,表面积增加了50.24平方厘米.若削成一个最大的圆锥体(如图,体积减少了多少立方厘米?
16.一个底面直径为20厘米,高为1米的圆木.
(1)如果沿着它的底面直径削开成两个同样的半圆柱,表面积增加
平方厘米.
(2)如果把它截成三个小圆柱体,表面积增加
平方厘米.
(3)如果把它的底面分成若干等份,然后沿高切开拼成一个近似的长方体,表面积增加了
平方厘米.
17.把一根长80厘米,底面半径是15厘米的圆柱形钢材锯成3段,表面积增加了多少平方厘米?
18.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
答案
1.解:水桶的侧面积:(平方分米),
水桶的底面积:(平方分米)
水桶的表面积:(平方分米),
铁皮的总面积:(平方分米)(平方米);
答:至少需要铁皮24.1平方米.
2.解:
(立方厘米),
答:它的体积是87.92立方厘米.
3.解:800千克吨,
(立方米),
(吨,
答:这个粮囤一共可以装38.1824吨粮食.
4.解:①
(立方厘米);
答:它的体积是320.28立方厘米.
②
(立方厘米);
答:它的体积是314立方厘米.
5.解:斜边上高:
答:绕斜边旋转一周后所形成的物体体积是30.144.
6.解:
(平方分米)
(立方分米)
答:这个图形的表面积是255.84平方分米,体积是25.12立方分米.
7.解:(1)表面积:
(平方厘米);
(2)体积:
(立方厘米);
答:它的表面积是251.2平方厘米,体积是251.2立方厘米.
8.解:
(立方厘米),
答:它的体积是2616立方厘米.
9.解:圆柱的半径是:
,
(厘米)
圆柱的体积:
(立方厘米)
答:这个圆柱的体积是141.3立方厘米.
10.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
11.解:
(立方厘米)
(毫升)
答:瓶子的容积是1256毫升.
12.解:(厘米),
(厘米),
,
,
(立方厘米);
答:这个瓶子的容积为2826立方厘米.
13.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
14.解:(厘米),
(厘米),
,
,
(毫升);
答:酒瓶容积是4019.2毫升.
15.解:(平方厘米);
,因为;
所以这个圆柱的底面半径是2厘米;
(厘米);
(立方厘米)
答:体积减少了25.12立方厘米.
16.解:1米厘米,
(1)(平方厘米);
答:表面积增加4000平方厘米.
(2)
(平方厘米);
答:表面积增加1256平方厘米.
(3)
(平方厘米);
答:表面积增加2000平方厘米.
故答案为:4000;1256;2000.
17.解:,
,
(平方厘米),
答:表面积增加了2826平方厘米.
18.解:圆锥的底面直径为:
(厘米);
则切割后表面积增加了:
(平方厘米);
答:表面积之和比原来圆锥表面积增加15平方厘米.
1.学校准备做12个无盖的圆柱体垃圾桶,底面直径为6分米,高8分米,至少需要铁皮多少平方米?(得数保留一位小数)
2.如图是在圆柱里挖去一个圆锥,求它的体积(单位:厘米)
3.一个粮囤如图所示,上面是圆锥形,下面是圆柱形.如果每立方米粮食重800千克.这个粮囤一共可以装多少吨粮食?
4.计算下面立体图形的体积(单位:
5.如图所示,直角三角形三条边分别长为3、4、5.求绕斜边旋转一周后所形成的物体体积.
6.求如图的表面积和体积.(单位:
7.如图是一种钢制的配件(图中数据单位:请计算它的表面积和体积.
8.一个零件,如图,求它的体积.取
9.一个圆柱的高是5厘米,如果截去一个高2厘米的小圆柱,原来圆柱的表面积就减少了37.68平方厘米,原来圆柱的体积是多少立方厘米?
10.有一个高8厘米,容量为50毫升的圆形容器,里面装满了水,现把长16厘米的圆柱垂直放入,使的底和的底面接触,这时一部分水从容器中溢出,当把从拿走后,中的水的高度只有6厘米,求圆柱体的体积是多少?
11.一个内直径是的瓶子里,水的高度是,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是.这个瓶子的容积是多少?
12.刘华测量一个瓶子的容积,测得瓶子的底面直径12厘米,然后给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,瓶子深30厘米.你能根据这些信息求出瓶子的容积吗?
13.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
14.如图,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒高15厘米.把酒瓶塞紧后,使其瓶口向下倒立,这时酒高19厘米,酒瓶容积是多少毫升?
15.一个圆柱形木块切成四块(如图,表面积增加48平方厘米;切成三块(如图,表面积增加了50.24平方厘米.若削成一个最大的圆锥体(如图,体积减少了多少立方厘米?
16.一个底面直径为20厘米,高为1米的圆木.
(1)如果沿着它的底面直径削开成两个同样的半圆柱,表面积增加
平方厘米.
(2)如果把它截成三个小圆柱体,表面积增加
平方厘米.
(3)如果把它的底面分成若干等份,然后沿高切开拼成一个近似的长方体,表面积增加了
平方厘米.
17.把一根长80厘米,底面半径是15厘米的圆柱形钢材锯成3段,表面积增加了多少平方厘米?
18.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
答案
1.解:水桶的侧面积:(平方分米),
水桶的底面积:(平方分米)
水桶的表面积:(平方分米),
铁皮的总面积:(平方分米)(平方米);
答:至少需要铁皮24.1平方米.
2.解:
(立方厘米),
答:它的体积是87.92立方厘米.
3.解:800千克吨,
(立方米),
(吨,
答:这个粮囤一共可以装38.1824吨粮食.
4.解:①
(立方厘米);
答:它的体积是320.28立方厘米.
②
(立方厘米);
答:它的体积是314立方厘米.
5.解:斜边上高:
答:绕斜边旋转一周后所形成的物体体积是30.144.
6.解:
(平方分米)
(立方分米)
答:这个图形的表面积是255.84平方分米,体积是25.12立方分米.
7.解:(1)表面积:
(平方厘米);
(2)体积:
(立方厘米);
答:它的表面积是251.2平方厘米,体积是251.2立方厘米.
8.解:
(立方厘米),
答:它的体积是2616立方厘米.
9.解:圆柱的半径是:
,
(厘米)
圆柱的体积:
(立方厘米)
答:这个圆柱的体积是141.3立方厘米.
10.解:圆形容器的底面积:
(平方厘米);
溢出水的体积,即放入容器的圆柱的体积:
,
,
(毫升);
圆柱体的体积是:
,
,
(立方厘米);
答:圆柱体的体积是25立方厘米.
11.解:
(立方厘米)
(毫升)
答:瓶子的容积是1256毫升.
12.解:(厘米),
(厘米),
,
,
(立方厘米);
答:这个瓶子的容积为2826立方厘米.
13.解:(厘米),
(立方厘米),
答:瓶内酸奶体积是25.92立方厘米.
14.解:(厘米),
(厘米),
,
,
(毫升);
答:酒瓶容积是4019.2毫升.
15.解:(平方厘米);
,因为;
所以这个圆柱的底面半径是2厘米;
(厘米);
(立方厘米)
答:体积减少了25.12立方厘米.
16.解:1米厘米,
(1)(平方厘米);
答:表面积增加4000平方厘米.
(2)
(平方厘米);
答:表面积增加1256平方厘米.
(3)
(平方厘米);
答:表面积增加2000平方厘米.
故答案为:4000;1256;2000.
17.解:,
,
(平方厘米),
答:表面积增加了2826平方厘米.
18.解:圆锥的底面直径为:
(厘米);
则切割后表面积增加了:
(平方厘米);
答:表面积之和比原来圆锥表面积增加15平方厘米.
