2020-2021学年八年级数学沪科版下册《第18章 勾股定理》单元测试卷(word版有答案)
文档属性
| 名称 | 2020-2021学年八年级数学沪科版下册《第18章 勾股定理》单元测试卷(word版有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览


文档简介
2020-2021学年沪科新版八年级下册数学《第18章 勾股定理》单元测试卷
一.选择题
1.直角三角形中有一锐角为15°,则另一锐角为( )
A.85° B.75° C.15° D.90°
2.对于任意两个正整数m、n(m>n),下列各组三个数为勾股数的一组是( )
A.m2+mn,m2﹣1,2mn B.m2﹣n2,2mn,m2+n2
C.m+n,m﹣n,2mn D.n2﹣1,n2+mn,2mn
3.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
4.线段AB和CD互相垂直平分于O点,且OC=AB,顺次连接A,D,B,C,那么图中的等腰直角三角形共有( )
A.4个 B.6个 C.8个 D.10个
5.在y轴上,与点A(3,﹣2)的距离等于3的点有( )
A.1个 B.2个 C.4个 D.0个
6.已知点A(0,﹣1),M(1,2),N(﹣3,0),则射线AM和射线AN组成的角的度数( )
A.一定大于90° B.一定小于90°
C.一定等于90° D.以上三种情况都有可能
7.将一根长24厘米的筷子,置于底面直径为6厘米,高为10厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为( )厘米.
A.14 B.16 C.24﹣ D.24+
8.设长方体的长、宽、高分别是5分米、3分米、4分米,在长方体表面上从点M到点N处的最短的途径是( )
A.3+分米 B.10分米 C.分米 D.4分米
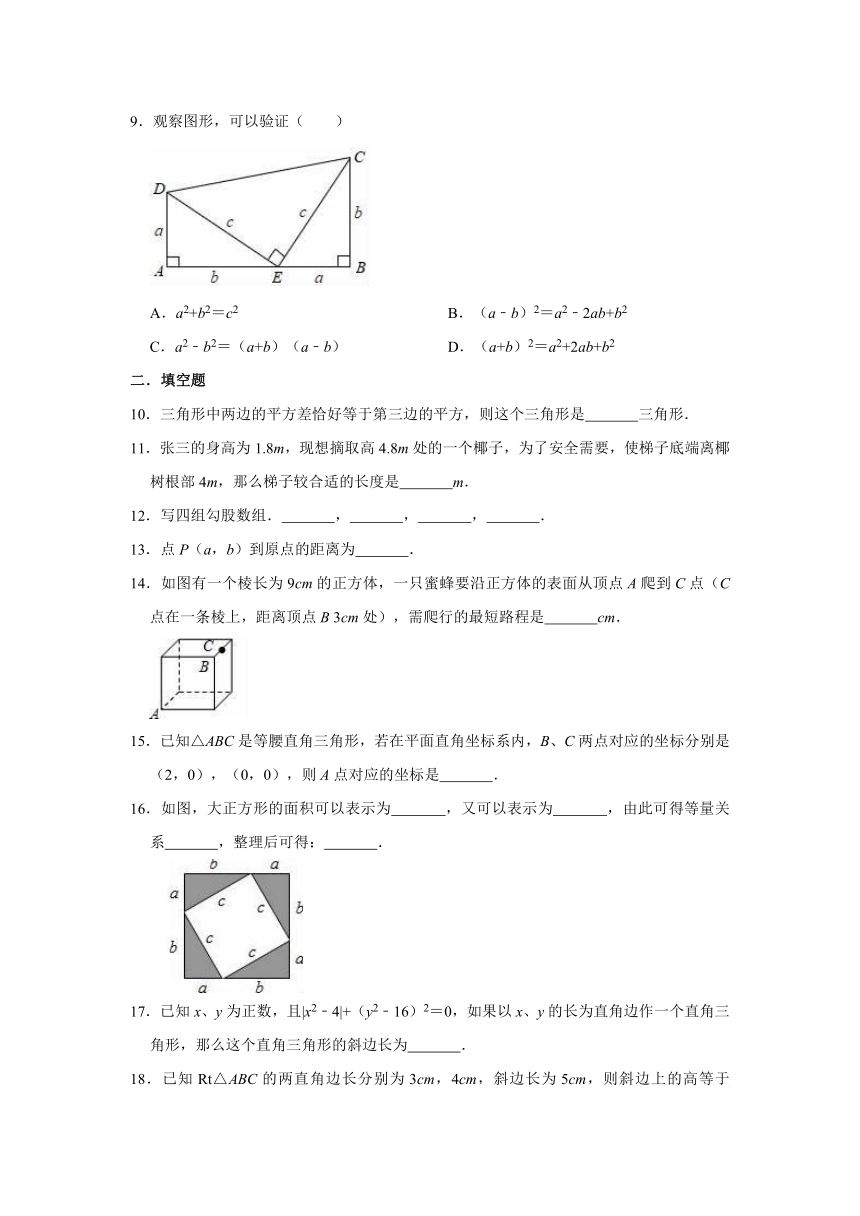
9.观察图形,可以验证( )
A.a2+b2=c2 B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b) D.(a+b)2=a2+2ab+b2
二.填空题
10.三角形中两边的平方差恰好等于第三边的平方,则这个三角形是 三角形.
11.张三的身高为1.8m,现想摘取高4.8m处的一个椰子,为了安全需要,使梯子底端离椰树根部4m,那么梯子较合适的长度是 m.
12.写四组勾股数组. , , , .
13.点P(a,b)到原点的距离为 .
14.如图有一个棱长为9cm的正方体,一只蜜蜂要沿正方体的表面从顶点A爬到C点(C点在一条棱上,距离顶点B 3cm处),需爬行的最短路程是 cm.
15.已知△ABC是等腰直角三角形,若在平面直角坐标系内,B、C两点对应的坐标分别是(2,0),(0,0),则A点对应的坐标是 .
16.如图,大正方形的面积可以表示为 ,又可以表示为 ,由此可得等量关系 ,整理后可得: .
17.已知x、y为正数,且|x2﹣4|+(y2﹣16)2=0,如果以x、y的长为直角边作一个直角三角形,那么这个直角三角形的斜边长为 .
18.已知Rt△ABC的两直角边长分别为3cm,4cm,斜边长为5cm,则斜边上的高等于 cm.
三.解答题
19.如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.试判断△ACD的形状,并说明理由.
20.奥地利数学家皮克发现了一个计算点阵中多边形面积的公式:S=a+b﹣1,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,请你根据下图,利用皮克公式探索一下勾股定理,看看是不是很简单.
21.如图,市政公司要安装一标志牌,要求标志牌与地面垂直,从地面高2m的B处向地面拉一根长2.5m的钢丝绳,钢丝绳在地面上的固定点A到标志牌底部C的距离为1.7m.请问该标志牌安装得是否符合要求?为什么?
22.如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米,自A至B在长方体表面的连线距离最短是多少?
23.如图,在△ABC中,∠BAC=2∠B,AB=2AC,求证:△ABC是直角三角形.
24.如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.
25.已知两点P1(﹣2,3),P2(4,﹣5),求P1、P2两点的距离.
参考答案与试题解析
一.选择题
1.解:∵直角三角形中有一锐角为15°,
根据直角三角形中两个锐角互余,
∴另一锐角=90°﹣15°=75°,
故选:B.
2.解:由勾股数的定义可得,满足两边的平方和等于第三边的平方即可,
而选项中只有B选项(m2﹣n2)2+(2mn)2=(m2+n2)2,
而A,C,D均不满足题意.
故选:B.
3.解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选:B.
4.解:∵线段AB和CD互相垂直平分于O点,
∴四边形ADBC是菱形,
∵OC=AB,
∴AB=CD,
∴四边形ADBC是正方形,
∴图中的每个三角形均为等腰直角三角形.
∴等腰直角三角形有:△ACO,△ADO,△BCO,△BDO,△ACB,△ADB,△ACD,△CBD.共8个.
故选:C.
5.解:在y轴上,与点A(3,﹣2)的距离等于3的点有(0,﹣2),
即只有1个点.
故选:A.
6.解:∵A(0,﹣1),M(1,2),N(﹣3,0),
∴AM==,
AN==,
MN==2,
∵()2+()2=(2)2,
∴射线AM和射线AN组成的角的度数一定等于90°.
7.解:如图所示,筷子,圆柱的高,圆柱的直径正好构成直角三角形,
在直角三角形ABC中,AC=10cm,BC=6cm,
则AB===cm,
故筷子露在杯子外面的长度至少为24﹣厘米.
故选:C.
8.解:(1)如图(1),
MN==;
(2)如图(2),
MN==;
(3)如图(3),
MN==
=4.
可见,MN的最小值为.
故选:C.
9.解:梯形面积=,
三个三角形面积之和=,
,
可得:c2=a2+b2,
故选:A.
二.填空题
10.解:设三角形的三边分别是a、b、c,则c2﹣a2=b2,
∴a2+b2=c2,
∴这个三角形是直角三角形.
故答案为:直角.
11.解:如图:椰子的高AC=4.8米,梯子底端距离椰树的根部BC=4米,
∵张三的身高为1.8米,
∴要想够到椰子CD=4.8﹣1.8=3米,
∴BD==5米,
故答案为:5
12.解:四组勾股数组可以是:3、4、5,5、12、13,7、24、25,9、40、41.
故答案为:3、4、5,5、12、13,7、24、25,9、40、41(答案不唯一).
13.解:如图,作PA⊥OA,连接OP.
∵P(a,b)
∴OA=|a|,PA=|b|,
∴OP=.故答案填:.
14.解:∵CD=9cm,AD=(3+9)cm,
∴AC===15cm,
故答案为:15.
15.解:如图所示:
由图可知,点A的坐标为(0,2),(0,﹣2),(1,1),(2,2),(2,﹣2)(1,﹣1).
故答案为(0,2),(0,﹣2),(1,1),(2,2),(2,﹣2)(1,﹣1).
16.解:大正方形的面积=(a+b)2,大正方形的面积=2ab+c2,则(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.
故答案为:(a+b)2;2ab+c2;(a+b)2=2ab+c2;a2+b2=c2.
17.解:由题意得,x2﹣4=0,y2﹣16=0,
所以,x2=4,y2=16,
由勾股定理得,斜边的平方=x2+y2=4+16=20,
所以,斜边==2.
故答案为:2.
18.解:如图,AC=3cm,BC=4cm,AB=5cm,CD为斜边AB上的高
∵S△ABC=AC?BC=CD?AB,
∴×3×4=×5?CD
∴CD=2.4cm.
三.解答题
19.解:△ACD是直角三角形.理由是:
∵∠B=90°,AB=3,BC=4,∴AC2=AB2+BC2=9+16=25,∴AC=5,
又∵AC2+CD2=25+144=169,AD2=169,∴AC2+CD2=AD2,
∴△ACD是直角三角形.
20.解:设三个正方形的面积从小到大是m,n,p.根据皮克公式,得:
m=2﹣1=1;
n=1+2﹣1=2;
p=2+2﹣1=3;
则m+n=p.
所以根据正方形的面积公式即证明了勾股定理.
21.解:该标志牌安装得不符合要求.
理由是:依题意,可知BC=2,AC=1.7,AB=2.5,
∵BC2+AB2=22+1.72=6.89,AC2=2.52=6.25,
∴BC2+AB2≠AC2,
∴△ABC不是Rt△,
∴该标志牌安装得不符合要求.
22.解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===25cm;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5cm;
只要把长方体的右侧表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB===5cm;
∵25<5<5,
∴自A至B在长方体表面的连线距离最短是25cm.
23.证明:如图,作线段AB的垂直平分线,垂足为D,且与BC相交于点E,易证△AED≌△BED.
∴AD=AB=×2AC=AC,∠B=∠EAD.
∵∠BAC=2∠B,∠EAD+∠EAC=∠BAC,
∴∠EAC=∠EAD.
在△AEC和△AED中,AE=AE,∠EAC=∠EAD,AC=AD,
∴△AEC≌△AED.
∴∠C=∠EDA.
∵∠EDA=90°,
∴∠C=90°.
故△ABC是直角三角形.
24.解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形;
③△CBE与△BED不全等,理由同②;
④△ACE与△ADE不全等,它们只有一边一角对应相等.
25.解:如图所示,
过P1、P2分别作x轴、y轴的垂线相交于A点.
则A点的坐标为A(﹣2,﹣5)
∴P1A=|﹣5﹣3|=8,P2A=|﹣2﹣4|=6,
∴P1P2===10.
一.选择题
1.直角三角形中有一锐角为15°,则另一锐角为( )
A.85° B.75° C.15° D.90°
2.对于任意两个正整数m、n(m>n),下列各组三个数为勾股数的一组是( )
A.m2+mn,m2﹣1,2mn B.m2﹣n2,2mn,m2+n2
C.m+n,m﹣n,2mn D.n2﹣1,n2+mn,2mn
3.在Rt△ABC中,a、b、c分别是∠A、∠B、∠C、的对边,若∠A=90°,则( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
4.线段AB和CD互相垂直平分于O点,且OC=AB,顺次连接A,D,B,C,那么图中的等腰直角三角形共有( )
A.4个 B.6个 C.8个 D.10个
5.在y轴上,与点A(3,﹣2)的距离等于3的点有( )
A.1个 B.2个 C.4个 D.0个
6.已知点A(0,﹣1),M(1,2),N(﹣3,0),则射线AM和射线AN组成的角的度数( )
A.一定大于90° B.一定小于90°
C.一定等于90° D.以上三种情况都有可能
7.将一根长24厘米的筷子,置于底面直径为6厘米,高为10厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为( )厘米.
A.14 B.16 C.24﹣ D.24+
8.设长方体的长、宽、高分别是5分米、3分米、4分米,在长方体表面上从点M到点N处的最短的途径是( )
A.3+分米 B.10分米 C.分米 D.4分米
9.观察图形,可以验证( )
A.a2+b2=c2 B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b) D.(a+b)2=a2+2ab+b2
二.填空题
10.三角形中两边的平方差恰好等于第三边的平方,则这个三角形是 三角形.
11.张三的身高为1.8m,现想摘取高4.8m处的一个椰子,为了安全需要,使梯子底端离椰树根部4m,那么梯子较合适的长度是 m.
12.写四组勾股数组. , , , .
13.点P(a,b)到原点的距离为 .
14.如图有一个棱长为9cm的正方体,一只蜜蜂要沿正方体的表面从顶点A爬到C点(C点在一条棱上,距离顶点B 3cm处),需爬行的最短路程是 cm.
15.已知△ABC是等腰直角三角形,若在平面直角坐标系内,B、C两点对应的坐标分别是(2,0),(0,0),则A点对应的坐标是 .
16.如图,大正方形的面积可以表示为 ,又可以表示为 ,由此可得等量关系 ,整理后可得: .
17.已知x、y为正数,且|x2﹣4|+(y2﹣16)2=0,如果以x、y的长为直角边作一个直角三角形,那么这个直角三角形的斜边长为 .
18.已知Rt△ABC的两直角边长分别为3cm,4cm,斜边长为5cm,则斜边上的高等于 cm.
三.解答题
19.如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.试判断△ACD的形状,并说明理由.
20.奥地利数学家皮克发现了一个计算点阵中多边形面积的公式:S=a+b﹣1,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,请你根据下图,利用皮克公式探索一下勾股定理,看看是不是很简单.
21.如图,市政公司要安装一标志牌,要求标志牌与地面垂直,从地面高2m的B处向地面拉一根长2.5m的钢丝绳,钢丝绳在地面上的固定点A到标志牌底部C的距离为1.7m.请问该标志牌安装得是否符合要求?为什么?
22.如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米,自A至B在长方体表面的连线距离最短是多少?
23.如图,在△ABC中,∠BAC=2∠B,AB=2AC,求证:△ABC是直角三角形.
24.如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.
25.已知两点P1(﹣2,3),P2(4,﹣5),求P1、P2两点的距离.
参考答案与试题解析
一.选择题
1.解:∵直角三角形中有一锐角为15°,
根据直角三角形中两个锐角互余,
∴另一锐角=90°﹣15°=75°,
故选:B.
2.解:由勾股数的定义可得,满足两边的平方和等于第三边的平方即可,
而选项中只有B选项(m2﹣n2)2+(2mn)2=(m2+n2)2,
而A,C,D均不满足题意.
故选:B.
3.解:如图所示,
∵∠A=90°,
∴b2+c2=a2.
故选:B.
4.解:∵线段AB和CD互相垂直平分于O点,
∴四边形ADBC是菱形,
∵OC=AB,
∴AB=CD,
∴四边形ADBC是正方形,
∴图中的每个三角形均为等腰直角三角形.
∴等腰直角三角形有:△ACO,△ADO,△BCO,△BDO,△ACB,△ADB,△ACD,△CBD.共8个.
故选:C.
5.解:在y轴上,与点A(3,﹣2)的距离等于3的点有(0,﹣2),
即只有1个点.
故选:A.
6.解:∵A(0,﹣1),M(1,2),N(﹣3,0),
∴AM==,
AN==,
MN==2,
∵()2+()2=(2)2,
∴射线AM和射线AN组成的角的度数一定等于90°.
7.解:如图所示,筷子,圆柱的高,圆柱的直径正好构成直角三角形,
在直角三角形ABC中,AC=10cm,BC=6cm,
则AB===cm,
故筷子露在杯子外面的长度至少为24﹣厘米.
故选:C.
8.解:(1)如图(1),
MN==;
(2)如图(2),
MN==;
(3)如图(3),
MN==
=4.
可见,MN的最小值为.
故选:C.
9.解:梯形面积=,
三个三角形面积之和=,
,
可得:c2=a2+b2,
故选:A.
二.填空题
10.解:设三角形的三边分别是a、b、c,则c2﹣a2=b2,
∴a2+b2=c2,
∴这个三角形是直角三角形.
故答案为:直角.
11.解:如图:椰子的高AC=4.8米,梯子底端距离椰树的根部BC=4米,
∵张三的身高为1.8米,
∴要想够到椰子CD=4.8﹣1.8=3米,
∴BD==5米,
故答案为:5
12.解:四组勾股数组可以是:3、4、5,5、12、13,7、24、25,9、40、41.
故答案为:3、4、5,5、12、13,7、24、25,9、40、41(答案不唯一).
13.解:如图,作PA⊥OA,连接OP.
∵P(a,b)
∴OA=|a|,PA=|b|,
∴OP=.故答案填:.
14.解:∵CD=9cm,AD=(3+9)cm,
∴AC===15cm,
故答案为:15.
15.解:如图所示:
由图可知,点A的坐标为(0,2),(0,﹣2),(1,1),(2,2),(2,﹣2)(1,﹣1).
故答案为(0,2),(0,﹣2),(1,1),(2,2),(2,﹣2)(1,﹣1).
16.解:大正方形的面积=(a+b)2,大正方形的面积=2ab+c2,则(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.
故答案为:(a+b)2;2ab+c2;(a+b)2=2ab+c2;a2+b2=c2.
17.解:由题意得,x2﹣4=0,y2﹣16=0,
所以,x2=4,y2=16,
由勾股定理得,斜边的平方=x2+y2=4+16=20,
所以,斜边==2.
故答案为:2.
18.解:如图,AC=3cm,BC=4cm,AB=5cm,CD为斜边AB上的高
∵S△ABC=AC?BC=CD?AB,
∴×3×4=×5?CD
∴CD=2.4cm.
三.解答题
19.解:△ACD是直角三角形.理由是:
∵∠B=90°,AB=3,BC=4,∴AC2=AB2+BC2=9+16=25,∴AC=5,
又∵AC2+CD2=25+144=169,AD2=169,∴AC2+CD2=AD2,
∴△ACD是直角三角形.
20.解:设三个正方形的面积从小到大是m,n,p.根据皮克公式,得:
m=2﹣1=1;
n=1+2﹣1=2;
p=2+2﹣1=3;
则m+n=p.
所以根据正方形的面积公式即证明了勾股定理.
21.解:该标志牌安装得不符合要求.
理由是:依题意,可知BC=2,AC=1.7,AB=2.5,
∵BC2+AB2=22+1.72=6.89,AC2=2.52=6.25,
∴BC2+AB2≠AC2,
∴△ABC不是Rt△,
∴该标志牌安装得不符合要求.
22.解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===25cm;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5cm;
只要把长方体的右侧表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB===5cm;
∵25<5<5,
∴自A至B在长方体表面的连线距离最短是25cm.
23.证明:如图,作线段AB的垂直平分线,垂足为D,且与BC相交于点E,易证△AED≌△BED.
∴AD=AB=×2AC=AC,∠B=∠EAD.
∵∠BAC=2∠B,∠EAD+∠EAC=∠BAC,
∴∠EAC=∠EAD.
在△AEC和△AED中,AE=AE,∠EAC=∠EAD,AC=AD,
∴△AEC≌△AED.
∴∠C=∠EDA.
∵∠EDA=90°,
∴∠C=90°.
故△ABC是直角三角形.
24.解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形;
③△CBE与△BED不全等,理由同②;
④△ACE与△ADE不全等,它们只有一边一角对应相等.
25.解:如图所示,
过P1、P2分别作x轴、y轴的垂线相交于A点.
则A点的坐标为A(﹣2,﹣5)
∴P1A=|﹣5﹣3|=8,P2A=|﹣2﹣4|=6,
∴P1P2===10.
