2020-2021学年度人教版八年级数学下册新考向多视角同步训练 专项训练卷三 平行四边形及特殊平行四边形的性质和判定(含解析)
文档属性
| 名称 | 2020-2021学年度人教版八年级数学下册新考向多视角同步训练 专项训练卷三 平行四边形及特殊平行四边形的性质和判定(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 16:34:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年度人教版八年级数学下册新考向多视角同步训练
专项训练卷(三)
平行四边形及特殊平行四边形的性质和判定
一、选择题
1.(2020广东佛山南海期末,5,★☆☆)小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是
(
)
A.对角线互相平分的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
2.(2020浙江台州中考,8,★☆☆)下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形下列推理过程正确的是
(
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
3.(2020山东菏泽曹县期末,5,★☆☆)如图,平行四边形ABCD中,对角线AC,BD相交于点O,下列条件:(1)∠1+
∠DBC=90°;(2)OA=OB;(3)∠1=∠2,其中能判定平行四边形ABCD是菱形的条件有
( )
A.0个
B.1个
C.2个
D.3个
4.(2020江苏淮安淮阴期中,8,★☆☆)如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形
ABCD面积的最大值是
(
)
A.15
B.16
C.19
D.20
5.(2020河南阳淅川期末,10,★★☆)如图,将长方形纸片ABCD沿BD折叠,使点C落在点C处,BC交AD于点E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中等腰三角形的个数(虚线也视为三角形的边)为
(
)
A.2
B.3
C.4
D.5
6.(2020山东枣庄薛城期末,7,★★☆)如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且
A(-3,0),B(2,b),则正方形ABCD的面积是
(
)
A.20
B.16
C.34
D.25
7.(2020北京二中期末,7,★★☆)小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具,成为如图①所示的菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具,成为如图②所示的正方形,则图②中对角线AC的长为
(
)
A.
20
cm
B.
30
cm
C.40
cm
D.20
cm
8.(2020江苏南京秦期中,8,★★☆)如图,在矩形D中,AB=4cm,AD=12cm点p在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒4cm的速度从点C出发,在C、B间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是
(
)
A.2
B.3
C.4
D.5
9.(2020江苏苏州高新期中,9,★★☆)如图,已知正方ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE的长为
(
)
A.2-2
B.-1
C.2-
D.-1
10.(2020山东泰安岱岳期中,11,★★☆)如图,在□ABCD中,按以下步骤作图:
①以点A为圆心,AB的长为半径作弧,交AD于点F;
②分别以点F,B为圆心,大于FB的长为半径作弧,两弧在∠DAB内交于点G;
③作射线AG,交边BC于点E,连接EF
若AB=5,BF=8,则四边形ABEF的面积为
(
)
A.12
B.20
C.24
D.48
二、填空题
11.(2020湖南邵阳中考,18,★★☆)如图,在Rt△ABC中,∠ACB=90°,斜边AB=,过点C作CF∥AB,以AB为边作菱形ABEF,若∠F=30°,则Rt△ABC的面积为________
12.(2020浙江杭州十三中模拟,16,★★☆)如图,在菱形ABCD中,边AB=5,E,F分别在边BC和AD上,若DF=1,BE=3,且BF=DE,则BF的长为________
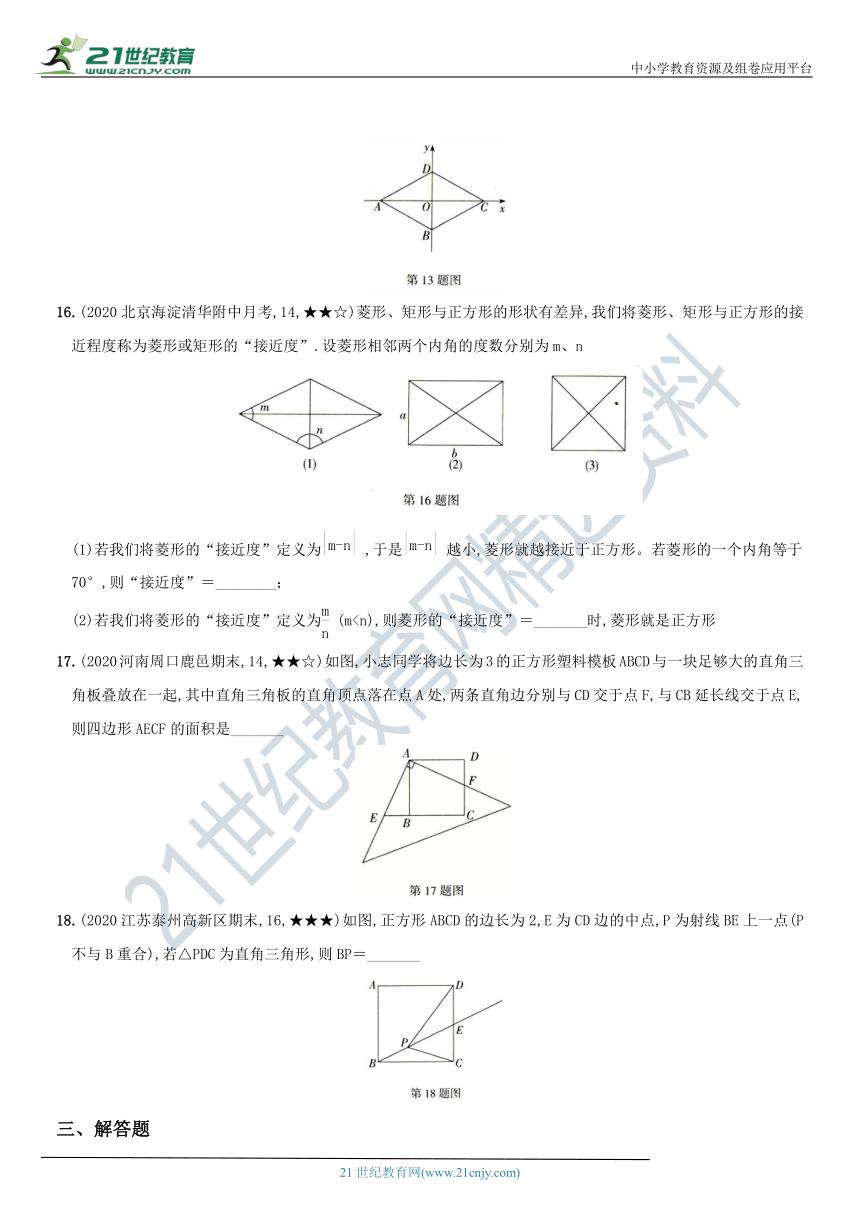
13.(2020辽宁沈阳皇姑一模,15,★★☆)如图,已知菱形ABCD顶点A(-,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标是________
14.(2020河北唐山一模,19,★★☆)有一边长为10m的正三角形(△ABC)游乐场,某人从边AB的中点P出发,先由点P沿平行于BC的方向运动到AC边上的点P1处,再由P沿平行于AB的方向运动到BC边上的点P2处又由点
P2沿平行于AC的方向运动到AB边上的点P3处(如图(1),则此人至少要运动________m,才能回到点P如果此
人从AB边上任意一点出发,按照上面的规律运动,至少走________m,才能回到起点
15.如图,定义若菱形AECF与正方形ABCD的两个顶点A、C重合,另外两个顶点E、F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形。若正方形的周长为16,其内含菱形的边长是整数,则内含菱形的周长为
________;若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________。
16.(2020北京海淀清华附中月考,14,★★☆)菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.设菱形相邻两个内角的度数分别为m、n
(1)若我们将菱形的“接近度”定义为,于是越小,菱形就越接近于正方形。若菱形的一个内角等于
70°,则“接近度”=________;
(2)若我们将菱形的“接近度”定义为(m17.(2020河南周口鹿邑期末,14,★★☆)如图,小志同学将边长为3的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB延长线交于点E,则四边形AECF的面积是_______
18.(2020江苏泰州高新区期末,16,★★★)如图,正方形ABCD的边长为2,E为CD边的中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP=_______
三、解答题
19.(2020山东淄博中考,19,★☆☆)已知:如图,E是ABCD的边BC延长线上的一点,且CE=BC
求证:△ABC≌△DCE.
20.(2020黑龙江大庆中考,24,★★☆)如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长
21.(2020云南中考,22,★★☆)如图,四边形ABCD是菱形,点H为对角线AC的中点,点在AB的延长线上,CE⊥
AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F
(1)若∠BAD=60°,求证:四边形CEHF是菱形;
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积
22.(2020河南郑州一模,19,★★☆)在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF
(1)求证:AD=AF;
(2)填空:①当∠ACB=_______°时,四边形ADCF为正方形;
②连接DF,当∠ACB=________°时,四边形ABDF为菱形
23.(2020江苏扬州江都三模,26,★★★)阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙
四边形”.
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫做“美妙线”,四边形ABDC就称为
“美妙四边形”
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形其中是“美妙四边形”的有________个;
(2)四边形ABCD是“美妙四边形”,AB=3+,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积(画出图形并写
出解答过程)
24.(2020山东枣庄台儿庄期末,25,★★★)如图在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,
运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、
AQ、CP.设点P、Q运动的时间为t
s.
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)求(2)中菱形AQCP的周长和面积
【参考答案及解析】
专项训练卷(三)平行四边形及特殊平行四边形的性质与判定
选择题答案速查
1
2
3
4
5
6
7
8
9
10
A
A
C
A
B
C
D
C
D
C
1.A
∵O是AC、BD的中点,∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。故选A
2.A
对角线相等的四边形推不出是正方形或矩形,所以①→②,①→③错误,
故选项B,C,D错误,故选A.
3.C
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD∥BC,∴∠1=∠BCO,
若∠1+∠DBC=90°,则∠BCO+∠DBC=90°,∴∠BOC=90°,∴AC⊥BD,
∴四边形ABCD是菱形,故(1)能判定平行四边形ABCD是菱形;
若OA=OB,则AC=BD,∴四边形ABCD是矩形,故(2)不能判定平行四边形ABCD是菱形;
若∠1=∠2,则∠2=∠BCO,∴AB=CB,∴四边形ABCD是菱形,故(3)能判定平行四边形ABCD是菱形。故选C
4.A
如图1,作AE⊥BC于E,AF⊥CD于F,
∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形
∵两个矩形的宽都是3,∴AE=AF=3,
∵s四边形ABCD=AE·BC=AF·CD,∴BC=CD,∴平行四边形ABCD是菱形
如图2,当菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,
设AB=BC=x,则BG=9-x,
∵BC2=BC2+CG2,∴x2=(9-x)2+32,解得x=5,
∴四边形ABCD面积的最大值是5×3=15,故选A
5.B
由矩形的性质得∠ABC=∠A=∠C=90°,AD∥BC,∴∠BDE=∠DBC=22.5°
由折叠的性质得∠CBD=∠DBC=22.5,∠C′=∠C=90°,
∴∠CBC′=45°,∠C′BD=∠BDE,∴∠ABE=45°,△ABE、△BDE是等腰三角形,
∴∠C′ED=∠AEB=45°,∴△C′DE是等腰三角形,
∴题图中的等腰三角形有3个.故选B.
6.C
作BM⊥x轴于M
∵四边形ABCD是正方形
∴Ad=aB,∠DAB=90°
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,∴∠DAO=∠ABM.
在△DAO和△ABM中,,∴△DAO≌△ABM(AAS),∴OA=BM,OD=AM,
∵A(-3,0),B(2,b),∴OA=3,OM=2,∴OD=AM=5,
∴AD==,∴正方形ABCD的面积是34,故选C
7.D
题图①中,四边形ABCD是菱形,∴AB=BC,
∵∠B=60°,∴△ABC是等边三角形,∴AB=BC=AC=20cm,
题图②中四边形ABCD是正方形,∴AB=BC,∠B=90°,△ABC是等腰直角三角形,∴AC=AB=20cm故选D.
8.C
当AB∥PQ时,∵AP∥BQ,∴四边形ABQP为平行四边形,∴AP=BQ
∵点P运动的时间=12÷1=12秒,∴点Q运动的路程=4×12=48cm.
∴点Q可以在B、C间往返2次
∴在这段时间内,PQ与AB有4次平行。
故选C.
9.D
∵四边形ABCD是正方形,AB=BC=CD=DA=1,∴∠BCD=90°
∴BD==
∵AC为正方形ABCD的对角线,CE平分∠ACD
∴∠BCE=67.5°,∠DCE=22.5°
∵∠BEC=∠EDC+∠DCE=45°+22.5°=67.5°,∴∠BEC=∠BCE,∴BC=BE,
∵BC=1,∴BE=1,∴DE=BD-BE=-1,故选D.
10.C
由作图可得直线AG是BF的垂直平分线,∴BO=FO,AE⊥FB,∠AFB=∠ABF,
∴BO=4,∴AO==3
∵四边形ABCD是平行四边形,∴AF∥BC,∴∠AFB=∠EBF,∴∠ABF=∠EBF,
在△AOB和△EOB中,,∴△AOB≌△EOB(ASA),∴AO=EO,
又BO=FO,∴四边形ABEF是平行四边形,
∴四边形ABEF的面积=4S△AOB=4×OA·BO=2×3×4=24
故选C.
11.答案:
解析:如图,分别过点E、C作EH、CG垂直于AB,垂足分别为点H、G,
∵四边形ABEF为菱形,AB=BE=,AB∥CF,
又∵∠ABE=30°,∴在Rt△BHE中,EH=
eq
\f(,2)
根据平行线间的距离处处相等知,
HE=CG=
eq
\f(,2)
,
∴Rt△ABC的面积为××
eq
\f(,2)
=,故答案为
12.答案:
解析∵在菱形ABCD中,AB=5,DF=1,BE=3,∴CE=2,AF=4,
如图,在AF上截取AG=CE=2,过点B作BH⊥FG于点H,
则FG=AF-AG=2,在菱形ABCD中,∠A=∠C,AB=DC,∴在△BAG和△DCE中,
,∴△BAG≌△DCE(SAS)∴BG=DE,
∵BF=DE,∴BG=BF
易知FH=HG=FG=1,
∴AH=AG+GH=2+1=3,
∵AB=5,∴在Rt△ABH中,由勾股定理得BH=4,
∴在Rt△BHF中,由勾股定理得BF===
)
.故答案为17.
13.答案:(0,-1)
解析∵在菱形ABCD中,∠DAB=60°,∴∠OAD=30°,
∵A(-,0),∴在Rt△AOD中,OA=,∵∠OAD=30°,∴AD=2OD,
由勾股定理得OD2+OA2=AD2,可得OD=1,∴AD=2,
∵动点P绕菱形一周的时间为2×4÷0.5=16(秒),
而2020÷16=126……4,∴第2020秒时,点P运动到点B处,
∵OB=OD=1,∴此时点P的坐标为(0,-1).故答案为(0,-1)
14.答案:15;30
解析:如题图(1),若某人从边AB的中点P出发,
∵P是AB的中点,AB=10m,∴AP=BP=5m,
∵PP1∥BC,P1P2∥AB,PP2∥AC,∴四边形BPP1P2是平行四边形,四边形PP1CP2是平行四边形,
∴PP1=BP2=P2C=5m,
同理可得P2P1=5m,P2P=5m,
∴PP1+P2P1+P2P=15m,
∴此人至少要运动15m,才能回到点P;
如题图(2),若某人从边AB上任意一点出发,
同理可得:四边形BPP1P2是平行四边形,四边形PP1CP5是平行四边形,
四边形AP3P2P1是平行四边形,四边形APP5P4是平行四边形,四边形P3P4CP2是平行四边形,
∴
PP1=
BP2,P1P2=BP,PP5=P1C,P4P5=AP,P2P3=AP1,P3P4=P2C,
∵PP1+P1P2+P2P3+P3P4+P4P5+P5P=BP2+BP+AP1+P2C+AP+P1C=AB+AC+BC=30
m.
故答案为15;30.
15.答案:12;
解析:如图,连接AC,BD,设AC、BD交于点O,
∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,
∵四边形AECF是菱形,∴EF⊥AC,
∵正方形ABCD的周长为16,∴AB=4,
∴20A2=16,∴OA=2,2∵内含菱形AECF的边长是整数,∴AE=3,
∴内含菱形的周长为12;
若正方形的面积为18,则AB=3,∴OA=3,
∵内含菱形AECF的面积为6,∴6=×6×EF,∴EF=2,
则内含菱形的边长为=.故答案为12;.
16.答案:(1)40°;(2)1
解析:(1)∵菱形的一个内角等于70°,∴与其相邻的另一个内角的度数为110°,
∴“接近度”等于=40°
(2)当菱形的“接近度”等于1时,菱形中相邻的两个内角相等,因而都是90度,则菱形就是正方形
故答案为40°;1.
17.答案:9
解析:∵四边形ABCD为正方形,∴∠D=∠ABC=90°,AD=AB,
∴∠ABE=∠D=90°,∵∠EAF=90°,∴∠DAF+∠BAF=90°,∠BAE+∠BAF=90°∴∠DAF=∠BAE,
在△AEB和△AFD中,,∴△AEB≌△AFD(ASA),∴S△AEB+S四边形ABCF
=S△AFD
+S四边形ABCF,
∴四边形AECF的面积=正方形ABCD的面积=9.故答案为9
18.答案:-1或+1或2
解析:分三种情况:
①如图1,当∠DPC=90°时,
∵E是CD的中点,且CD=2,∴PE=CD=1,
∵四边形ABCD是正方形,∴BC=2,∠BCD=90°,
∴BE==,∴BP=BE-PE=-1.
②如图2,当∠DPC=90°时,
同理可得BP=+1.
③如图3,当∠CDP=90°时,
∵∠BCE=∠EDP=90°,DE=CE,∠BEC=∠DEP,∴△BCE≌△PDE(ASA),
∴PE=BE=,∴BP=2.
综上可得,BP的长是-1或+1或2.
19.证明:四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,,∴△ABC≌△DCE(SAS).
20.解析:(1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,∴∠OAM=∠OCN,∠OMA=∠ONC,
在△AOM和△CON中,,∴△AOM≌△CON(AAS),∴AM=CN,
∵AM∥CN,∴四边形ANCM为平行四边形
(2)∵在矩形ABCD中,AD=BC,
由(1)知AM=CN,∴DM=BN,
∵四边形ANCM为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,∴AM=AN=NC=AD-DM,
∴在Rt△ABN中,根据勾股定理,得AN2=AB2+BN2,
∴(4-DM)2=22+DM2,解得DM=
21.解析:(1)证明:∵四边形ABCD是菱形,∠BAD=60°,
∴∠EAC=∠FAC=30°,
又∵CE⊥AB,CF⊥AD,∴CE=CF=AC,
∵点H为对角线AC的中点,∴EH=fh=AC
∴CE=CF=EH=FH,∴四边形CEHF是菱形
(2)∵CE⊥AB,CE=4,△ACE的面积为16,∴AE=8,
∴AC==4,
如图,连接BD,则BD⊥AC,AH=AC=2,
设AB=x,则BC=x,EB=8-x,
在Rt△ECB中,EB2+EC2=BC2,(8-x)2+42=x2,
解得x=5,∴S△ECB=×3×4=6,
∴菱形ABCD的面积=2(S△ACE-S△ECB)=20
22.解析:(1)证明:∵∠BAC=90°,AD是BC边上的中线,∴AD=CD=BD,
∵点E为AD的中点,∴AE=DE,
∵AF∥BC,∴∠AFE=∠DBE,
又∵∠AEF=∠DEB,∴△AEF≌△DEB(AAS),
∴AF=BD,∴AD=AF
(2)①当∠ACB=45°时,四边形ADCF为正方形
∵AD=AF,∴AF=CD
∵AF∥CD,∴四边形ADCF是菱形,∴∠ACD=∠ACF=45°,∴∠DCF=90°,∴四边形ADCF是正方形
②如图,当∠ACB=30°时,四边形ABDF为菱形
∵四边形ADCF是菱形,∴CD=CF,∠ACB=∠ACF=30°,
∴∠DCF=60°,∴△DCF是等边三角形,∴DF=CD,∴DF=BD,
又∵四边形ABDF是平行四边形,∴四边形ABDF为菱形
23.解析:(1)∵菱形和正方形的每一条对角线平分一组对角,
∴菱形和正方形是“美妙四边形”,有2个.
(2)分两种情况:
①当AC是“美妙线”时,如图1,
∵AC平分∠BAD、∠BCD,∠BAD=60°,∴∠BAC=∠BAD=30°
在△ABC中,∠B=90°,AB=3+,∴BC=+1,
∵∠B=90°,∠BAC=30°,∴∠ACB=60°,∴∠ACD=60°,
∵∠CAD=∠BAC=30°,∴∠D=90°,
∵,∴△ABC≌△ADC(AAS),
∴S四边形ABCD=2s△ABC=2×(3+)×(+1)=6+4
②当BD是“美妙线”时,如图2,过D作DH⊥AB于H,
∵∠ABC=90°,BD平分∠ABC,∴∠ABD=∠CBD=45°∴△BDH是等腰直角三角形,∴DH=BH,
设AH=a,∵∠BAD=60°,∴∠ADH=30°,∴AD=2a,∴DH=a,
∴BH=a,∴AB=AH+BH=a+a=3+,
∴a=,∴DH=3,
易证△ABD≌△CBD,
∴S四边形ABCD=2S△ABD=2×AB·DH=3×(3+)=9+3
综上所述,四边形ABCD的面积为6+4或9+3
24.解析:(1)∵在矩形ABCD中,AB=8cm,BC=16cm,
∴BC=AD=16
cm,
AB
=CD=8
cm,
由已知可得,BQ=DP=t
cm,AP=CQ=(16-t)cm,
在矩形ABCD中,∠B=90°,AD∥BC
当BQ=AP时,四边形ABQP为矩形
∴t=16-t,解得t=8,
故当t=8时,四边形ABQP为矩形
(2)∵AP=CQ,AP∥CQ,∴四边形AQCP为平行四边形,
∴当AQ=CQ时,四边形AQCP为菱形,
=16-t,解得t=6,故当t=6时,四边形AQCP为菱形
(3)当t=6时,AQ=CQ=CP=AP=16-6=10cm,则菱形AQCP的周长为4×10=40cm,
面积为10×8=80cm2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年度人教版八年级数学下册新考向多视角同步训练
专项训练卷(三)
平行四边形及特殊平行四边形的性质和判定
一、选择题
1.(2020广东佛山南海期末,5,★☆☆)小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是
(
)
A.对角线互相平分的四边形是平行四边形
B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
2.(2020浙江台州中考,8,★☆☆)下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形下列推理过程正确的是
(
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
3.(2020山东菏泽曹县期末,5,★☆☆)如图,平行四边形ABCD中,对角线AC,BD相交于点O,下列条件:(1)∠1+
∠DBC=90°;(2)OA=OB;(3)∠1=∠2,其中能判定平行四边形ABCD是菱形的条件有
( )
A.0个
B.1个
C.2个
D.3个
4.(2020江苏淮安淮阴期中,8,★☆☆)如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形
ABCD面积的最大值是
(
)
A.15
B.16
C.19
D.20
5.(2020河南阳淅川期末,10,★★☆)如图,将长方形纸片ABCD沿BD折叠,使点C落在点C处,BC交AD于点E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中等腰三角形的个数(虚线也视为三角形的边)为
(
)
A.2
B.3
C.4
D.5
6.(2020山东枣庄薛城期末,7,★★☆)如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且
A(-3,0),B(2,b),则正方形ABCD的面积是
(
)
A.20
B.16
C.34
D.25
7.(2020北京二中期末,7,★★☆)小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具,成为如图①所示的菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具,成为如图②所示的正方形,则图②中对角线AC的长为
(
)
A.
20
cm
B.
30
cm
C.40
cm
D.20
cm
8.(2020江苏南京秦期中,8,★★☆)如图,在矩形D中,AB=4cm,AD=12cm点p在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒4cm的速度从点C出发,在C、B间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是
(
)
A.2
B.3
C.4
D.5
9.(2020江苏苏州高新期中,9,★★☆)如图,已知正方ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE的长为
(
)
A.2-2
B.-1
C.2-
D.-1
10.(2020山东泰安岱岳期中,11,★★☆)如图,在□ABCD中,按以下步骤作图:
①以点A为圆心,AB的长为半径作弧,交AD于点F;
②分别以点F,B为圆心,大于FB的长为半径作弧,两弧在∠DAB内交于点G;
③作射线AG,交边BC于点E,连接EF
若AB=5,BF=8,则四边形ABEF的面积为
(
)
A.12
B.20
C.24
D.48
二、填空题
11.(2020湖南邵阳中考,18,★★☆)如图,在Rt△ABC中,∠ACB=90°,斜边AB=,过点C作CF∥AB,以AB为边作菱形ABEF,若∠F=30°,则Rt△ABC的面积为________
12.(2020浙江杭州十三中模拟,16,★★☆)如图,在菱形ABCD中,边AB=5,E,F分别在边BC和AD上,若DF=1,BE=3,且BF=DE,则BF的长为________
13.(2020辽宁沈阳皇姑一模,15,★★☆)如图,已知菱形ABCD顶点A(-,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标是________
14.(2020河北唐山一模,19,★★☆)有一边长为10m的正三角形(△ABC)游乐场,某人从边AB的中点P出发,先由点P沿平行于BC的方向运动到AC边上的点P1处,再由P沿平行于AB的方向运动到BC边上的点P2处又由点
P2沿平行于AC的方向运动到AB边上的点P3处(如图(1),则此人至少要运动________m,才能回到点P如果此
人从AB边上任意一点出发,按照上面的规律运动,至少走________m,才能回到起点
15.如图,定义若菱形AECF与正方形ABCD的两个顶点A、C重合,另外两个顶点E、F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形。若正方形的周长为16,其内含菱形的边长是整数,则内含菱形的周长为
________;若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________。
16.(2020北京海淀清华附中月考,14,★★☆)菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.设菱形相邻两个内角的度数分别为m、n
(1)若我们将菱形的“接近度”定义为,于是越小,菱形就越接近于正方形。若菱形的一个内角等于
70°,则“接近度”=________;
(2)若我们将菱形的“接近度”定义为(m
18.(2020江苏泰州高新区期末,16,★★★)如图,正方形ABCD的边长为2,E为CD边的中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP=_______
三、解答题
19.(2020山东淄博中考,19,★☆☆)已知:如图,E是ABCD的边BC延长线上的一点,且CE=BC
求证:△ABC≌△DCE.
20.(2020黑龙江大庆中考,24,★★☆)如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN
(1)求证:四边形ANCM为平行四边形;
(2)若AD=4,AB=2,且MN⊥AC,求DM的长
21.(2020云南中考,22,★★☆)如图,四边形ABCD是菱形,点H为对角线AC的中点,点在AB的延长线上,CE⊥
AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F
(1)若∠BAD=60°,求证:四边形CEHF是菱形;
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积
22.(2020河南郑州一模,19,★★☆)在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF
(1)求证:AD=AF;
(2)填空:①当∠ACB=_______°时,四边形ADCF为正方形;
②连接DF,当∠ACB=________°时,四边形ABDF为菱形
23.(2020江苏扬州江都三模,26,★★★)阅读理解题.
定义:如果四边形的某条对角线平分一组对角,那么把这条对角线叫做“美妙线”,该四边形叫做“美妙
四边形”.
如图,在四边形ABDC中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫做“美妙线”,四边形ABDC就称为
“美妙四边形”
问题:
(1)下列四边形:平行四边形、矩形、菱形、正方形其中是“美妙四边形”的有________个;
(2)四边形ABCD是“美妙四边形”,AB=3+,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积(画出图形并写
出解答过程)
24.(2020山东枣庄台儿庄期末,25,★★★)如图在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,
运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、
AQ、CP.设点P、Q运动的时间为t
s.
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)求(2)中菱形AQCP的周长和面积
【参考答案及解析】
专项训练卷(三)平行四边形及特殊平行四边形的性质与判定
选择题答案速查
1
2
3
4
5
6
7
8
9
10
A
A
C
A
B
C
D
C
D
C
1.A
∵O是AC、BD的中点,∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)。故选A
2.A
对角线相等的四边形推不出是正方形或矩形,所以①→②,①→③错误,
故选项B,C,D错误,故选A.
3.C
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD∥BC,∴∠1=∠BCO,
若∠1+∠DBC=90°,则∠BCO+∠DBC=90°,∴∠BOC=90°,∴AC⊥BD,
∴四边形ABCD是菱形,故(1)能判定平行四边形ABCD是菱形;
若OA=OB,则AC=BD,∴四边形ABCD是矩形,故(2)不能判定平行四边形ABCD是菱形;
若∠1=∠2,则∠2=∠BCO,∴AB=CB,∴四边形ABCD是菱形,故(3)能判定平行四边形ABCD是菱形。故选C
4.A
如图1,作AE⊥BC于E,AF⊥CD于F,
∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形
∵两个矩形的宽都是3,∴AE=AF=3,
∵s四边形ABCD=AE·BC=AF·CD,∴BC=CD,∴平行四边形ABCD是菱形
如图2,当菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,
设AB=BC=x,则BG=9-x,
∵BC2=BC2+CG2,∴x2=(9-x)2+32,解得x=5,
∴四边形ABCD面积的最大值是5×3=15,故选A
5.B
由矩形的性质得∠ABC=∠A=∠C=90°,AD∥BC,∴∠BDE=∠DBC=22.5°
由折叠的性质得∠CBD=∠DBC=22.5,∠C′=∠C=90°,
∴∠CBC′=45°,∠C′BD=∠BDE,∴∠ABE=45°,△ABE、△BDE是等腰三角形,
∴∠C′ED=∠AEB=45°,∴△C′DE是等腰三角形,
∴题图中的等腰三角形有3个.故选B.
6.C
作BM⊥x轴于M
∵四边形ABCD是正方形
∴Ad=aB,∠DAB=90°
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,∴∠DAO=∠ABM.
在△DAO和△ABM中,,∴△DAO≌△ABM(AAS),∴OA=BM,OD=AM,
∵A(-3,0),B(2,b),∴OA=3,OM=2,∴OD=AM=5,
∴AD==,∴正方形ABCD的面积是34,故选C
7.D
题图①中,四边形ABCD是菱形,∴AB=BC,
∵∠B=60°,∴△ABC是等边三角形,∴AB=BC=AC=20cm,
题图②中四边形ABCD是正方形,∴AB=BC,∠B=90°,△ABC是等腰直角三角形,∴AC=AB=20cm故选D.
8.C
当AB∥PQ时,∵AP∥BQ,∴四边形ABQP为平行四边形,∴AP=BQ
∵点P运动的时间=12÷1=12秒,∴点Q运动的路程=4×12=48cm.
∴点Q可以在B、C间往返2次
∴在这段时间内,PQ与AB有4次平行。
故选C.
9.D
∵四边形ABCD是正方形,AB=BC=CD=DA=1,∴∠BCD=90°
∴BD==
∵AC为正方形ABCD的对角线,CE平分∠ACD
∴∠BCE=67.5°,∠DCE=22.5°
∵∠BEC=∠EDC+∠DCE=45°+22.5°=67.5°,∴∠BEC=∠BCE,∴BC=BE,
∵BC=1,∴BE=1,∴DE=BD-BE=-1,故选D.
10.C
由作图可得直线AG是BF的垂直平分线,∴BO=FO,AE⊥FB,∠AFB=∠ABF,
∴BO=4,∴AO==3
∵四边形ABCD是平行四边形,∴AF∥BC,∴∠AFB=∠EBF,∴∠ABF=∠EBF,
在△AOB和△EOB中,,∴△AOB≌△EOB(ASA),∴AO=EO,
又BO=FO,∴四边形ABEF是平行四边形,
∴四边形ABEF的面积=4S△AOB=4×OA·BO=2×3×4=24
故选C.
11.答案:
解析:如图,分别过点E、C作EH、CG垂直于AB,垂足分别为点H、G,
∵四边形ABEF为菱形,AB=BE=,AB∥CF,
又∵∠ABE=30°,∴在Rt△BHE中,EH=
eq
\f(,2)
根据平行线间的距离处处相等知,
HE=CG=
eq
\f(,2)
,
∴Rt△ABC的面积为××
eq
\f(,2)
=,故答案为
12.答案:
解析∵在菱形ABCD中,AB=5,DF=1,BE=3,∴CE=2,AF=4,
如图,在AF上截取AG=CE=2,过点B作BH⊥FG于点H,
则FG=AF-AG=2,在菱形ABCD中,∠A=∠C,AB=DC,∴在△BAG和△DCE中,
,∴△BAG≌△DCE(SAS)∴BG=DE,
∵BF=DE,∴BG=BF
易知FH=HG=FG=1,
∴AH=AG+GH=2+1=3,
∵AB=5,∴在Rt△ABH中,由勾股定理得BH=4,
∴在Rt△BHF中,由勾股定理得BF===
)
.故答案为17.
13.答案:(0,-1)
解析∵在菱形ABCD中,∠DAB=60°,∴∠OAD=30°,
∵A(-,0),∴在Rt△AOD中,OA=,∵∠OAD=30°,∴AD=2OD,
由勾股定理得OD2+OA2=AD2,可得OD=1,∴AD=2,
∵动点P绕菱形一周的时间为2×4÷0.5=16(秒),
而2020÷16=126……4,∴第2020秒时,点P运动到点B处,
∵OB=OD=1,∴此时点P的坐标为(0,-1).故答案为(0,-1)
14.答案:15;30
解析:如题图(1),若某人从边AB的中点P出发,
∵P是AB的中点,AB=10m,∴AP=BP=5m,
∵PP1∥BC,P1P2∥AB,PP2∥AC,∴四边形BPP1P2是平行四边形,四边形PP1CP2是平行四边形,
∴PP1=BP2=P2C=5m,
同理可得P2P1=5m,P2P=5m,
∴PP1+P2P1+P2P=15m,
∴此人至少要运动15m,才能回到点P;
如题图(2),若某人从边AB上任意一点出发,
同理可得:四边形BPP1P2是平行四边形,四边形PP1CP5是平行四边形,
四边形AP3P2P1是平行四边形,四边形APP5P4是平行四边形,四边形P3P4CP2是平行四边形,
∴
PP1=
BP2,P1P2=BP,PP5=P1C,P4P5=AP,P2P3=AP1,P3P4=P2C,
∵PP1+P1P2+P2P3+P3P4+P4P5+P5P=BP2+BP+AP1+P2C+AP+P1C=AB+AC+BC=30
m.
故答案为15;30.
15.答案:12;
解析:如图,连接AC,BD,设AC、BD交于点O,
∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,
∵四边形AECF是菱形,∴EF⊥AC,
∵正方形ABCD的周长为16,∴AB=4,
∴20A2=16,∴OA=2,2
∴内含菱形的周长为12;
若正方形的面积为18,则AB=3,∴OA=3,
∵内含菱形AECF的面积为6,∴6=×6×EF,∴EF=2,
则内含菱形的边长为=.故答案为12;.
16.答案:(1)40°;(2)1
解析:(1)∵菱形的一个内角等于70°,∴与其相邻的另一个内角的度数为110°,
∴“接近度”等于=40°
(2)当菱形的“接近度”等于1时,菱形中相邻的两个内角相等,因而都是90度,则菱形就是正方形
故答案为40°;1.
17.答案:9
解析:∵四边形ABCD为正方形,∴∠D=∠ABC=90°,AD=AB,
∴∠ABE=∠D=90°,∵∠EAF=90°,∴∠DAF+∠BAF=90°,∠BAE+∠BAF=90°∴∠DAF=∠BAE,
在△AEB和△AFD中,,∴△AEB≌△AFD(ASA),∴S△AEB+S四边形ABCF
=S△AFD
+S四边形ABCF,
∴四边形AECF的面积=正方形ABCD的面积=9.故答案为9
18.答案:-1或+1或2
解析:分三种情况:
①如图1,当∠DPC=90°时,
∵E是CD的中点,且CD=2,∴PE=CD=1,
∵四边形ABCD是正方形,∴BC=2,∠BCD=90°,
∴BE==,∴BP=BE-PE=-1.
②如图2,当∠DPC=90°时,
同理可得BP=+1.
③如图3,当∠CDP=90°时,
∵∠BCE=∠EDP=90°,DE=CE,∠BEC=∠DEP,∴△BCE≌△PDE(ASA),
∴PE=BE=,∴BP=2.
综上可得,BP的长是-1或+1或2.
19.证明:四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,,∴△ABC≌△DCE(SAS).
20.解析:(1)证明:∵在矩形ABCD中,O为对角线AC的中点,
∴AD∥BC,AO=CO,∴∠OAM=∠OCN,∠OMA=∠ONC,
在△AOM和△CON中,,∴△AOM≌△CON(AAS),∴AM=CN,
∵AM∥CN,∴四边形ANCM为平行四边形
(2)∵在矩形ABCD中,AD=BC,
由(1)知AM=CN,∴DM=BN,
∵四边形ANCM为平行四边形,MN⊥AC,
∴平行四边形ANCM为菱形,∴AM=AN=NC=AD-DM,
∴在Rt△ABN中,根据勾股定理,得AN2=AB2+BN2,
∴(4-DM)2=22+DM2,解得DM=
21.解析:(1)证明:∵四边形ABCD是菱形,∠BAD=60°,
∴∠EAC=∠FAC=30°,
又∵CE⊥AB,CF⊥AD,∴CE=CF=AC,
∵点H为对角线AC的中点,∴EH=fh=AC
∴CE=CF=EH=FH,∴四边形CEHF是菱形
(2)∵CE⊥AB,CE=4,△ACE的面积为16,∴AE=8,
∴AC==4,
如图,连接BD,则BD⊥AC,AH=AC=2,
设AB=x,则BC=x,EB=8-x,
在Rt△ECB中,EB2+EC2=BC2,(8-x)2+42=x2,
解得x=5,∴S△ECB=×3×4=6,
∴菱形ABCD的面积=2(S△ACE-S△ECB)=20
22.解析:(1)证明:∵∠BAC=90°,AD是BC边上的中线,∴AD=CD=BD,
∵点E为AD的中点,∴AE=DE,
∵AF∥BC,∴∠AFE=∠DBE,
又∵∠AEF=∠DEB,∴△AEF≌△DEB(AAS),
∴AF=BD,∴AD=AF
(2)①当∠ACB=45°时,四边形ADCF为正方形
∵AD=AF,∴AF=CD
∵AF∥CD,∴四边形ADCF是菱形,∴∠ACD=∠ACF=45°,∴∠DCF=90°,∴四边形ADCF是正方形
②如图,当∠ACB=30°时,四边形ABDF为菱形
∵四边形ADCF是菱形,∴CD=CF,∠ACB=∠ACF=30°,
∴∠DCF=60°,∴△DCF是等边三角形,∴DF=CD,∴DF=BD,
又∵四边形ABDF是平行四边形,∴四边形ABDF为菱形
23.解析:(1)∵菱形和正方形的每一条对角线平分一组对角,
∴菱形和正方形是“美妙四边形”,有2个.
(2)分两种情况:
①当AC是“美妙线”时,如图1,
∵AC平分∠BAD、∠BCD,∠BAD=60°,∴∠BAC=∠BAD=30°
在△ABC中,∠B=90°,AB=3+,∴BC=+1,
∵∠B=90°,∠BAC=30°,∴∠ACB=60°,∴∠ACD=60°,
∵∠CAD=∠BAC=30°,∴∠D=90°,
∵,∴△ABC≌△ADC(AAS),
∴S四边形ABCD=2s△ABC=2×(3+)×(+1)=6+4
②当BD是“美妙线”时,如图2,过D作DH⊥AB于H,
∵∠ABC=90°,BD平分∠ABC,∴∠ABD=∠CBD=45°∴△BDH是等腰直角三角形,∴DH=BH,
设AH=a,∵∠BAD=60°,∴∠ADH=30°,∴AD=2a,∴DH=a,
∴BH=a,∴AB=AH+BH=a+a=3+,
∴a=,∴DH=3,
易证△ABD≌△CBD,
∴S四边形ABCD=2S△ABD=2×AB·DH=3×(3+)=9+3
综上所述,四边形ABCD的面积为6+4或9+3
24.解析:(1)∵在矩形ABCD中,AB=8cm,BC=16cm,
∴BC=AD=16
cm,
AB
=CD=8
cm,
由已知可得,BQ=DP=t
cm,AP=CQ=(16-t)cm,
在矩形ABCD中,∠B=90°,AD∥BC
当BQ=AP时,四边形ABQP为矩形
∴t=16-t,解得t=8,
故当t=8时,四边形ABQP为矩形
(2)∵AP=CQ,AP∥CQ,∴四边形AQCP为平行四边形,
∴当AQ=CQ时,四边形AQCP为菱形,
=16-t,解得t=6,故当t=6时,四边形AQCP为菱形
(3)当t=6时,AQ=CQ=CP=AP=16-6=10cm,则菱形AQCP的周长为4×10=40cm,
面积为10×8=80cm2
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
