第4章数列 章末复习2020-2021学年高二数学人教A版(2019)选择性必修2
文档属性
| 名称 | 第4章数列 章末复习2020-2021学年高二数学人教A版(2019)选择性必修2 |  | |
| 格式 | doc | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 17:37:51 | ||
图片预览




文档简介
知识系统整合
规律方法收藏
1.由数列的前n项和求an时,应注意是
an=若an=Sn-Sn-1(n≥2)对于n=1也成立,则合并写成一个an的式子,否则分段表示an.
2.使用an-an-1=d(常数)或=q(常数)证明等差或等比数列时,以上两式中均应注明(n≥2,n∈N*),否则,数列不是等差数列或等比数列.
3.牢记等差、等比数列的一些重要性质并应用,往往能迅速地解决问题,但是不要忘记解等差、等比数列问题常用的基本量法,才是通用方法.
4.使用等比数列前n项和公式时,应注意公比q是否等于1.
5.等差、等比数列的通项公式和前n项和公式是它们的重要基本公式,对这两个公式要用方程思想、函数思想并从变形与发展的角度去深刻认识.
6.解等差、等比数列的综合题必须牢固掌握基础知识、基本技能和基本题型,并且要灵活运用这些知识,善于将综合题分解为几个基本题.解等差、等比数列的应用题,关键是将抽象的文字语言转化为数学语言,应用数列的定义、公式及性质加以解决.这就要求能真正理解题意、理清其脉络,从纷繁复杂的实际问题中发掘出其本质特征.
7.应用数列知识解应用题,应首先读懂题意,然后建立数学模型,最后求解、回答.
8.判断数列{an}为等差数列的充要条件
(1)数列{an}是等差数列?an-an-1=d(n≥2).
(2)数列{an}是等差数列?2an=an+1+an-1(n≥2).
(3)数列{an}是等差数列?an=pn+q(p,q是与n无关的常数).
(4)数列{an}是等差数列?a1+a2+…+an=An2+Bn(A,B为常数).
9.等差数列与等比数列的转换
(1)若数列{an}是等差数列,则数列{aan}(a>0,a≠1)是等比数列.
(2)若数列{an}是等比数列,则数列{lg |an|}是等差数列.
10.数学归纳法的运用关键在于对归纳原理的深刻理解.
学科思想培优
一、数列通项公式的求法
数列的通项公式是数列的核心之一,它如同函数中的解析式一样,有解析式便可研究函数的性质,而有了数列的通项公式,便可求出数列中的任何一项及前n项和.常见的数列通项公式的求法有以下几种:
1 观察归纳法求数列的通项公式
就是观察数列的特征,横向看各项之间的关系结构,纵向看各项与序号n的内在联系,结合常见数列的通项公式,归纳出所求数列的通项公式.
2 利用公式法求数列的通项公式
数列符合等差数列或等比数列的定义,求通项时,只需求出a1与d或a1与q,再代入公式an=a1+(n-1)d或an=a1qn-1中即可.
3 利用an与Sn的关系求数列的通项公式
如果给出的条件是an与Sn的关系式,可利用an=先求出a1=S1,再通过计算求出an(n≥2)的关系式,检验当n=1时,a1是否满足该式,若不满足该式,则an要分段表示.
4 利用累加法、累乘法求数列的通项公式
形如:已知a1,且an+1-an=f(n)(f(n)是可求和数列)的形式均可用累加法;
形如:已知a1,且=f(n)(f(n)是可求积数列)的形式均可用累乘法.
5 构造法(利用数列的递推公式研究数列的通项公式)
若由已知条件直接求an较难,可以通过整理变形等,从中构造出一个等差数列或等比数列,从而求出通项公式.
[典例1] 数列{an}中,an+1=2an+1,且a1=1,求通项公式an.
[典例2] 在数列{an}中,已知a1=2且an+1=4an-3n+1,求通项公式an.
[典例3] 已知数列{an}满足an+1=2an+3×5n,a1=2,求数列{an}的通项公式.
[典例4] 已知数列{an}中,a1=,an+1=,求数列{an}的通项公式.
[典例5] 设Sn为数列{an}的前n项的和,且Sn=(an-1)(n∈N*),求数列{an}的通项公式.
[典例6] 在数列{an}中,a1=2,an+1=an,求通项公式an.
二、以数阵为背景的数列问题
1 数阵的特点
所谓数阵是指将某些数,按一定的规律排成若干行和列,形成图表,也称之为数表,例如大家都非常熟悉的“杨辉三角”.数阵不仅有正方形、三角形,还有长方形、圆、多边形、星形、花瓣形、十字形,甚至几种图形的组合,变幻多样、对称性强,很能吸引人.在我们平常解题中最常见的是前两种.
2 以数阵为背景的数列问题
数阵中的数是按一定的规律排成若干行和列,比较多见的是排成等差或等比数列,它重点考查等差、等比数列的相关知识,有时也会出现其他类型的数列,解决此类问题的关键是找出其中的规律,这就要求考生要有较强的观察、归纳、猜想能力以及对数列知识的融合迁移能力,下面例谈一下它的几种题型.
题型一 求数阵所暗示的规律(即通项公式)
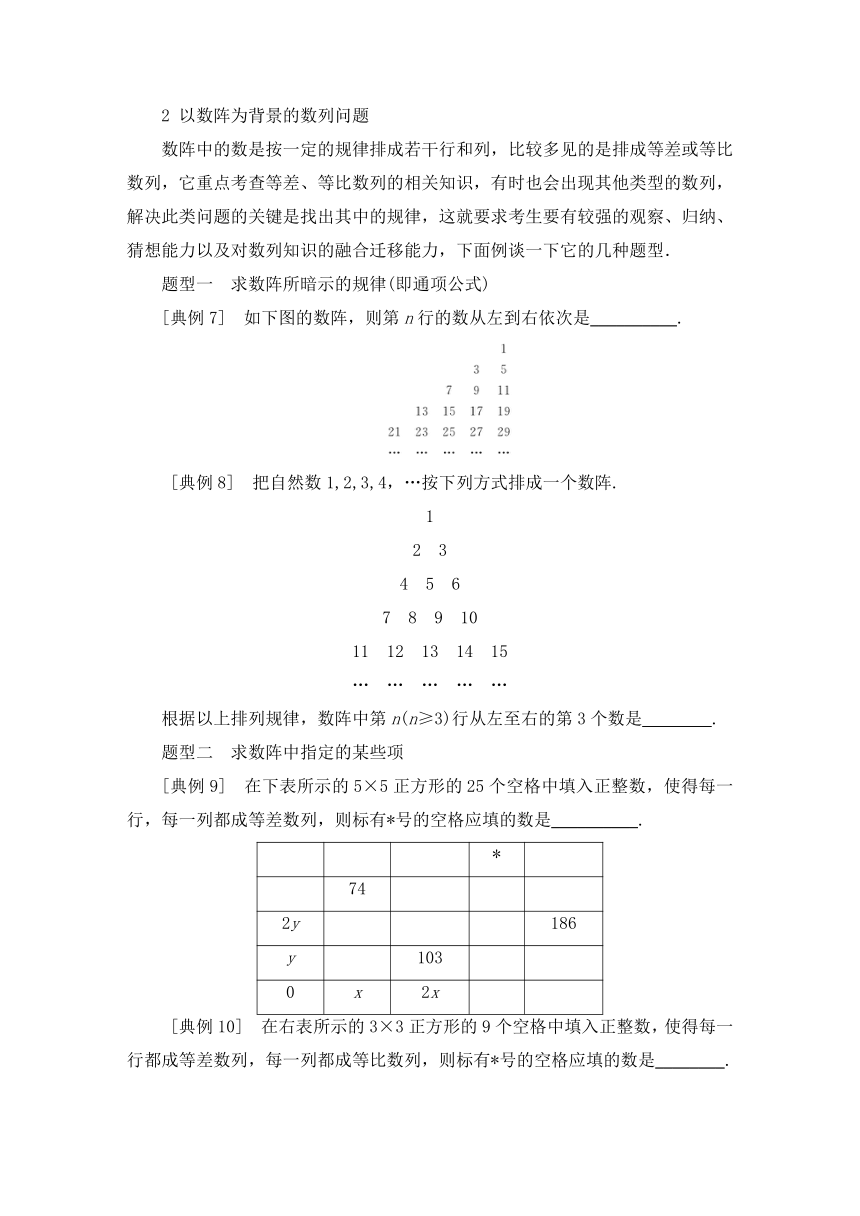
[典例7] 如下图的数阵,则第n行的数从左到右依次是__________.
[典例8] 把自然数1,2,3,4,…按下列方式排成一个数阵.
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … …
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
题型二 求数阵中指定的某些项
[典例9] 在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,则标有*号的空格应填的数是__________.
*
74
2y
186
y
103
0 x 2x
[典例10] 在右表所示的3×3正方形的9个空格中填入正整数,使得每一行都成等差数列,每一列都成等比数列,则标有*号的空格应填的数是________.
1
3
*
12
题型三 求数阵中某指定项的位置
[典例11] 自然数按下图所示规律排列,问2020是第几行第几个数?
题型四 求数阵中所有项或某些指定项的和
[典例12] 给定81个数排成数阵如下图所示,若每一行,每一列都构成等差数列,且正中间一个数a55=5,则此数阵中所有数之和为__________.
三、数列中的数学思想与方法
1 函数与方程思想
由于数列可以看作定义域为正整数集或正整数集的有限子集的函数an=f(n),数列中的项是自变量从小到大取值时对应的一列函数值,因此在研究某些数列问题时,利用函数思想既有利于理解问题的本质,又简化了运算,如求等差数列前n项和的最值时,构建二次函数则简洁明了,求数列的最大项或最小项,可以根据函数的单调性求出最值.
[典例13] 设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=21,S15=-75,Tn为数列的前n项和,求Tn的最大值.
2 化归、转化思想
等差数列、等比数列的计算,一般先求a1,公差d或公比q;遇到an与Sn的关系时,可以利用an=Sn-Sn-1(n≥2)都转化为an或Sn,再转化为等差数列或等比数列,利用等差或等比数列的通项公式求出.其中合理的转化是解题的关键.
[典例14] 设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(n=2,3,4,…),求数列{bn}的通项bn;
(3)求和:b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
3 整体思想
解决某些数列问题时,往往要将其中的某一局部结构视为一个整体,利用整体思想简化结构,从而简化数列的运算.
[典例15] 已知等差数列{an}的前四项之和为-4,最后四项之和为36,且所有项之和为36,求其项数.
4 分类讨论思想
数列中某些问题往往需利用分类讨论思想来解决,如等比数列的前n项和公式中,若公比q的取值未知,则需要对q=1与q≠1分类求解;由Sn求an时应分n=1和n≥2两种情况讨论;某些数列的前n项和也需要讨论,通过分类讨论可以将复杂问题简单化,解题时要注意分类讨论标准的确定,做到不重不漏.
[典例16] 已知等比数列{an}的各项均为正数,2a5,a4,4a6成等差数列,且满足a4=4a,数列{bn}的前n项和Sn=bn,n∈N*,且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=求数列{cn}的前n项和Pn;
(3)设dn=an,n∈N*,数列{dn}的前n项和为Tn,求证:Tn<.
5 由有限到无限的思想
数学归纳法的基本原理,即归纳原理(也称多米诺骨牌效应)通过研究有限来洞察无限,实现了由有限到无限的数学飞跃.
[典例17] 已知数列{an}满足a2=6,=(n∈N*).
(1)求a1,a3,a4,a5的值;
(2)猜想{an}的通项公式,并用数学归纳法证明.
知识系统整合
规律方法收藏
1.由数列的前n项和求an时,应注意是
an=若an=Sn-Sn-1(n≥2)对于n=1也成立,则合并写成一个an的式子,否则分段表示an.
2.使用an-an-1=d(常数)或=q(常数)证明等差或等比数列时,以上两式中均应注明(n≥2,n∈N*),否则,数列不是等差数列或等比数列.
3.牢记等差、等比数列的一些重要性质并应用,往往能迅速地解决问题,但是不要忘记解等差、等比数列问题常用的基本量法,才是通用方法.
4.使用等比数列前n项和公式时,应注意公比q是否等于1.
5.等差、等比数列的通项公式和前n项和公式是它们的重要基本公式,对这两个公式要用方程思想、函数思想并从变形与发展的角度去深刻认识.
6.解等差、等比数列的综合题必须牢固掌握基础知识、基本技能和基本题型,并且要灵活运用这些知识,善于将综合题分解为几个基本题.解等差、等比数列的应用题,关键是将抽象的文字语言转化为数学语言,应用数列的定义、公式及性质加以解决.这就要求能真正理解题意、理清其脉络,从纷繁复杂的实际问题中发掘出其本质特征.
7.应用数列知识解应用题,应首先读懂题意,然后建立数学模型,最后求解、回答.
8.判断数列{an}为等差数列的充要条件
(1)数列{an}是等差数列?an-an-1=d(n≥2).
(2)数列{an}是等差数列?2an=an+1+an-1(n≥2).
(3)数列{an}是等差数列?an=pn+q(p,q是与n无关的常数).
(4)数列{an}是等差数列?a1+a2+…+an=An2+Bn(A,B为常数).
9.等差数列与等比数列的转换
(1)若数列{an}是等差数列,则数列{aan}(a>0,a≠1)是等比数列.
(2)若数列{an}是等比数列,则数列{lg |an|}是等差数列.
10.数学归纳法的运用关键在于对归纳原理的深刻理解.
学科思想培优
一、数列通项公式的求法
数列的通项公式是数列的核心之一,它如同函数中的解析式一样,有解析式便可研究函数的性质,而有了数列的通项公式,便可求出数列中的任何一项及前n项和.常见的数列通项公式的求法有以下几种:
1 观察归纳法求数列的通项公式
就是观察数列的特征,横向看各项之间的关系结构,纵向看各项与序号n的内在联系,结合常见数列的通项公式,归纳出所求数列的通项公式.
2 利用公式法求数列的通项公式
数列符合等差数列或等比数列的定义,求通项时,只需求出a1与d或a1与q,再代入公式an=a1+(n-1)d或an=a1qn-1中即可.
3 利用an与Sn的关系求数列的通项公式
如果给出的条件是an与Sn的关系式,可利用an=先求出a1=S1,再通过计算求出an(n≥2)的关系式,检验当n=1时,a1是否满足该式,若不满足该式,则an要分段表示.
4 利用累加法、累乘法求数列的通项公式
形如:已知a1,且an+1-an=f(n)(f(n)是可求和数列)的形式均可用累加法;
形如:已知a1,且=f(n)(f(n)是可求积数列)的形式均可用累乘法.
5 构造法(利用数列的递推公式研究数列的通项公式)
若由已知条件直接求an较难,可以通过整理变形等,从中构造出一个等差数列或等比数列,从而求出通项公式.
[典例1] 数列{an}中,an+1=2an+1,且a1=1,求通项公式an.
[解] 解法一:(迭代法)
an=2an-1+1=2(2an-2+1)+1=22an-2+2×1+1=23an-3+22×1+2×1+1=…=2n-1a1+(2n-2+2n-3+…+2+1)=2n-1+2n-2+…+2+1=2n-1.
解法二:(待定系数法)
由an+1=2an+1,
设an+1+k=2(an+k),∴an+1=2an+k,∴k=1,
∴{an+1}为等比数列,∴a1+1=2,公比为2,
∴an+1=2×2n-1,∴an=2n-1.
解法三:(累加法)
由an+1=2an+1,an=2an-1+1,得
an+1-an=2(an-an-1)(n≥2).
故{an+1-an}是首项为a2-a1=2,公比为2的等比数列,即an+1-an=2·2n-1=2n,
利用累加得an=2n-1.
[典例2] 在数列{an}中,已知a1=2且an+1=4an-3n+1,求通项公式an.
[解] 令an+1-A(n+1)-B=4(an-An-B),
则an+1=4an-3An+A-3B.
由条件得解得
即an+1-(n+1)=4(an-n),故数列{an-n}是首项为a1-1=1,公比为4的等比数列,从而an-n=4n-1,故an=4n-1+n.
[典例3] 已知数列{an}满足an+1=2an+3×5n,a1=2,求数列{an}的通项公式.
[解] 两边同除以5n+1,得=×+,
可得-1=.
由于-1=-≠0,所以数列是以-为首项,为公比的等比数列,从而-1=-×n-1,故数列{an}的通项公式为an=5n-3×2n-1.
[典例4] 已知数列{an}中,a1=,an+1=,求数列{an}的通项公式.
[解] 由题意,可得==+2,
又=,所以数列是首项为,公差为2的等差数列,故=+2(n-1)=,
所以数列{an}的通项公式为an=.
[典例5] 设Sn为数列{an}的前n项的和,且Sn=(an-1)(n∈N*),求数列{an}的通项公式.
[解] ∵Sn=(an-1),
∴当n=1时,S1=a1=(a1-1),解得a1=3.
当n≥2时,an=Sn-Sn-1=(an-1)-(an-1-1),得=3,∴数列{an}是以3为公比的等比数列,且首项a1=3.故数列的通项公式为an=3n(n∈N*).
[典例6] 在数列{an}中,a1=2,an+1=an,求通项公式an.
[解] ∵a1=2,an+1=an,
∴=,=,…,=,
以上n-1个等式左右两边分别相乘得=n·2n-1,即an=n·2n,且n=1时,a1=2也适合上式,
∴an=n·2n.
二、以数阵为背景的数列问题
1 数阵的特点
所谓数阵是指将某些数,按一定的规律排成若干行和列,形成图表,也称之为数表,例如大家都非常熟悉的“杨辉三角”.数阵不仅有正方形、三角形,还有长方形、圆、多边形、星形、花瓣形、十字形,甚至几种图形的组合,变幻多样、对称性强,很能吸引人.在我们平常解题中最常见的是前两种.
2 以数阵为背景的数列问题
数阵中的数是按一定的规律排成若干行和列,比较多见的是排成等差或等比数列,它重点考查等差、等比数列的相关知识,有时也会出现其他类型的数列,解决此类问题的关键是找出其中的规律,这就要求考生要有较强的观察、归纳、猜想能力以及对数列知识的融合迁移能力,下面例谈一下它的几种题型.
题型一 求数阵所暗示的规律(即通项公式)
[典例7] 如下图的数阵,则第n行的数从左到右依次是__________.
[解析] 设第n行左边第一个数为an,则a1=1,a2=3=a1+2×1,a3=7=a2+2×2,…,an=an-1+2(n-1).叠加得an=n2-n+1,故第n行的数从左到右依次是n2-n+1,n2-n+3,n2-n+5,…,n2-n+(2n-1).
[答案] n2-n+1,n2-n+3,n2-n+5,…,n2-n+(2n-1)
[典例8] 把自然数1,2,3,4,…按下列方式排成一个数阵.
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … …
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
[解析] 该数阵的第1行有1个数,第2行有2个数,…,第n行有n个数,则第n-1(n≥3)行的最后一个数为=-,则第n行从左至右的第3个数为-+3.
[答案] -+3
题型二 求数阵中指定的某些项
[典例9] 在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,则标有*号的空格应填的数是__________.
*
74
2y
186
y
103
0 x 2x
[解析] 记aij为第i行第j列的格中所填的数,则a52=x,a41=y.
由第3行得a33=,由第3列得a33=2×103-2x,所以2x+y=113.①
由第1列得a21=3y,则由第2行得a23=2×74-3y,由第3列得a33+103=a23+2x,所以a23=3×103-4x.所以2×74-3y=3×103-4x,即4x-3y=161,②
解①②,得x=50,y=13.所以a15=2×186-a55=2×186-4x=172,a13=2a33-a53=112,a14==142,故标有*号的空格应填142.
[答案] 142
[典例10] 在右表所示的3×3正方形的9个空格中填入正整数,使得每一行都成等差数列,每一列都成等比数列,则标有*号的空格应填的数是________.
1
3
*
12
[解析] 设标有*号的空格应填a,根据中间空格列方程,得×2=2,解得a=4,故标有*号的空格应填4.
[答案] 4
题型三 求数阵中某指定项的位置
[典例11] 自然数按下图所示规律排列,问2020是第几行第几个数?
[解] 设2020在第m行,则m是满足>2020的最小正整数,解得m=64.经分析知第64行左边第一个数是2017,则2020-2017+1=4,故2020是第64行第4个数.
题型四 求数阵中所有项或某些指定项的和
[典例12] 给定81个数排成数阵如下图所示,若每一行,每一列都构成等差数列,且正中间一个数a55=5,则此数阵中所有数之和为__________.
[解析] S=(a11+a12+…+a19)+(a21+a22+…+a29)+…+(a91+a92+…+a99)=9(a15+a25+…+a95)=9×9×a55=405.故此数阵中所有数之和为405.
[答案] 405
三、数列中的数学思想与方法
1 函数与方程思想
由于数列可以看作定义域为正整数集或正整数集的有限子集的函数an=f(n),数列中的项是自变量从小到大取值时对应的一列函数值,因此在研究某些数列问题时,利用函数思想既有利于理解问题的本质,又简化了运算,如求等差数列前n项和的最值时,构建二次函数则简洁明了,求数列的最大项或最小项,可以根据函数的单调性求出最值.
[典例13] 设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=21,S15=-75,Tn为数列的前n项和,求Tn的最大值.
[解] 设等差数列{an}的公差为d,则
Sn=na1+d,因为S7=21,S15=-75,
所以
解得
所以Sn=9n-(n2-n)=10n-n2,
所以=10-n.
因为-=-1,=9,所以数列是首项为9,公差为-1的等差数列,所以Tn==-n2+n=-2+.
因为n∈N*,所以当n=9或10时,Tn有最大值为45.
2 化归、转化思想
等差数列、等比数列的计算,一般先求a1,公差d或公比q;遇到an与Sn的关系时,可以利用an=Sn-Sn-1(n≥2)都转化为an或Sn,再转化为等差数列或等比数列,利用等差或等比数列的通项公式求出.其中合理的转化是解题的关键.
[典例14] 设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(n=2,3,4,…),求数列{bn}的通项bn;
(3)求和:b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
[解] (1)证明:∵a1=S1=1,S2=1+a2,
∴a2=,=.
又3tSn-(2t+3)Sn-1=3t,①
∴3tSn-1-(2t+3)Sn-2=3t(n≥3),②
①-②,得3tan-(2t+3)an-1=0,
∴=(n=2,3,…),
∴数列{an}是一个首项为1,公比为的等比数列.
(2)由f(t)==+,得
bn=f=+bn-1.
∴数列{bn}是一个首项为1,公差为的等差数列.
∴bn=1+(n-1)=.
(3)由bn=,可知{b2n-1}和{b2n}是首项分别为1和,公差均为的等差数列,
于是b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1=b2(b1-b3)+b4(b3-b5)+b6(b5-b7)+…+b2n(b2n-1-b2n+1)=-(b2+b4+…+b2n)=-×n×=-(2n2+3n).
3 整体思想
解决某些数列问题时,往往要将其中的某一局部结构视为一个整体,利用整体思想简化结构,从而简化数列的运算.
[典例15] 已知等差数列{an}的前四项之和为-4,最后四项之和为36,且所有项之和为36,求其项数.
[解] 由题意,得
①+②,得a1+a2+a3+a4+an+an-1+an-2+an-3=32,
∴4(a1+an)=32,∴a1+an=8.
又Sn==×8=36,∴n=9,
即该数列的项数为9.
4 分类讨论思想
数列中某些问题往往需利用分类讨论思想来解决,如等比数列的前n项和公式中,若公比q的取值未知,则需要对q=1与q≠1分类求解;由Sn求an时应分n=1和n≥2两种情况讨论;某些数列的前n项和也需要讨论,通过分类讨论可以将复杂问题简单化,解题时要注意分类讨论标准的确定,做到不重不漏.
[典例16] 已知等比数列{an}的各项均为正数,2a5,a4,4a6成等差数列,且满足a4=4a,数列{bn}的前n项和Sn=bn,n∈N*,且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=求数列{cn}的前n项和Pn;
(3)设dn=an,n∈N*,数列{dn}的前n项和为Tn,求证:Tn<.
[解] (1)因为an>0,所以q>0.
?
解得
所以an=n,
当n≥2时,bn=Sn-Sn-1=bn-,即=,
所以数列是首项为1的常数列,=1.
所以bn=n.
(2)由(1)可得cn=
当n为偶数时,Pn=(b1+b3+…+bn-1)+(a2+a4+…+an)
=[1+3+…+(n-1)]+
=(1+n-1)+
=+-·n;
当n为奇数时,Pn=Pn-1+bn=+-·n-1+n
=+-·n-1.
(3)证明:因为dn=·
=-,
所以Tn=-+-+…+-=-<.
5 由有限到无限的思想
数学归纳法的基本原理,即归纳原理(也称多米诺骨牌效应)通过研究有限来洞察无限,实现了由有限到无限的数学飞跃.
[典例17] 已知数列{an}满足a2=6,=(n∈N*).
(1)求a1,a3,a4,a5的值;
(2)猜想{an}的通项公式,并用数学归纳法证明.
[解] (1)∵a2=6,=,
当n=1时,=1,∴a1=1,
当n=2时,=,∴a3=15,
当n=3时,=,∴a4=28,
当n=4时,=,∴a5=45.
(2)由(1)猜想an=n(2n-1),证明如下:
①当n=1时,a1=1成立;
②假设n=k时,猜想成立,即ak=k(2k-1),
则当n=k+1时,有=,
化简,得ak+1=(k+1)(2k+1),
即当n=k+1时,猜想成立.
由①②可知,猜想对任意n∈N*都成立.
规律方法收藏
1.由数列的前n项和求an时,应注意是
an=若an=Sn-Sn-1(n≥2)对于n=1也成立,则合并写成一个an的式子,否则分段表示an.
2.使用an-an-1=d(常数)或=q(常数)证明等差或等比数列时,以上两式中均应注明(n≥2,n∈N*),否则,数列不是等差数列或等比数列.
3.牢记等差、等比数列的一些重要性质并应用,往往能迅速地解决问题,但是不要忘记解等差、等比数列问题常用的基本量法,才是通用方法.
4.使用等比数列前n项和公式时,应注意公比q是否等于1.
5.等差、等比数列的通项公式和前n项和公式是它们的重要基本公式,对这两个公式要用方程思想、函数思想并从变形与发展的角度去深刻认识.
6.解等差、等比数列的综合题必须牢固掌握基础知识、基本技能和基本题型,并且要灵活运用这些知识,善于将综合题分解为几个基本题.解等差、等比数列的应用题,关键是将抽象的文字语言转化为数学语言,应用数列的定义、公式及性质加以解决.这就要求能真正理解题意、理清其脉络,从纷繁复杂的实际问题中发掘出其本质特征.
7.应用数列知识解应用题,应首先读懂题意,然后建立数学模型,最后求解、回答.
8.判断数列{an}为等差数列的充要条件
(1)数列{an}是等差数列?an-an-1=d(n≥2).
(2)数列{an}是等差数列?2an=an+1+an-1(n≥2).
(3)数列{an}是等差数列?an=pn+q(p,q是与n无关的常数).
(4)数列{an}是等差数列?a1+a2+…+an=An2+Bn(A,B为常数).
9.等差数列与等比数列的转换
(1)若数列{an}是等差数列,则数列{aan}(a>0,a≠1)是等比数列.
(2)若数列{an}是等比数列,则数列{lg |an|}是等差数列.
10.数学归纳法的运用关键在于对归纳原理的深刻理解.
学科思想培优
一、数列通项公式的求法
数列的通项公式是数列的核心之一,它如同函数中的解析式一样,有解析式便可研究函数的性质,而有了数列的通项公式,便可求出数列中的任何一项及前n项和.常见的数列通项公式的求法有以下几种:
1 观察归纳法求数列的通项公式
就是观察数列的特征,横向看各项之间的关系结构,纵向看各项与序号n的内在联系,结合常见数列的通项公式,归纳出所求数列的通项公式.
2 利用公式法求数列的通项公式
数列符合等差数列或等比数列的定义,求通项时,只需求出a1与d或a1与q,再代入公式an=a1+(n-1)d或an=a1qn-1中即可.
3 利用an与Sn的关系求数列的通项公式
如果给出的条件是an与Sn的关系式,可利用an=先求出a1=S1,再通过计算求出an(n≥2)的关系式,检验当n=1时,a1是否满足该式,若不满足该式,则an要分段表示.
4 利用累加法、累乘法求数列的通项公式
形如:已知a1,且an+1-an=f(n)(f(n)是可求和数列)的形式均可用累加法;
形如:已知a1,且=f(n)(f(n)是可求积数列)的形式均可用累乘法.
5 构造法(利用数列的递推公式研究数列的通项公式)
若由已知条件直接求an较难,可以通过整理变形等,从中构造出一个等差数列或等比数列,从而求出通项公式.
[典例1] 数列{an}中,an+1=2an+1,且a1=1,求通项公式an.
[典例2] 在数列{an}中,已知a1=2且an+1=4an-3n+1,求通项公式an.
[典例3] 已知数列{an}满足an+1=2an+3×5n,a1=2,求数列{an}的通项公式.
[典例4] 已知数列{an}中,a1=,an+1=,求数列{an}的通项公式.
[典例5] 设Sn为数列{an}的前n项的和,且Sn=(an-1)(n∈N*),求数列{an}的通项公式.
[典例6] 在数列{an}中,a1=2,an+1=an,求通项公式an.
二、以数阵为背景的数列问题
1 数阵的特点
所谓数阵是指将某些数,按一定的规律排成若干行和列,形成图表,也称之为数表,例如大家都非常熟悉的“杨辉三角”.数阵不仅有正方形、三角形,还有长方形、圆、多边形、星形、花瓣形、十字形,甚至几种图形的组合,变幻多样、对称性强,很能吸引人.在我们平常解题中最常见的是前两种.
2 以数阵为背景的数列问题
数阵中的数是按一定的规律排成若干行和列,比较多见的是排成等差或等比数列,它重点考查等差、等比数列的相关知识,有时也会出现其他类型的数列,解决此类问题的关键是找出其中的规律,这就要求考生要有较强的观察、归纳、猜想能力以及对数列知识的融合迁移能力,下面例谈一下它的几种题型.
题型一 求数阵所暗示的规律(即通项公式)
[典例7] 如下图的数阵,则第n行的数从左到右依次是__________.
[典例8] 把自然数1,2,3,4,…按下列方式排成一个数阵.
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … …
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
题型二 求数阵中指定的某些项
[典例9] 在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,则标有*号的空格应填的数是__________.
*
74
2y
186
y
103
0 x 2x
[典例10] 在右表所示的3×3正方形的9个空格中填入正整数,使得每一行都成等差数列,每一列都成等比数列,则标有*号的空格应填的数是________.
1
3
*
12
题型三 求数阵中某指定项的位置
[典例11] 自然数按下图所示规律排列,问2020是第几行第几个数?
题型四 求数阵中所有项或某些指定项的和
[典例12] 给定81个数排成数阵如下图所示,若每一行,每一列都构成等差数列,且正中间一个数a55=5,则此数阵中所有数之和为__________.
三、数列中的数学思想与方法
1 函数与方程思想
由于数列可以看作定义域为正整数集或正整数集的有限子集的函数an=f(n),数列中的项是自变量从小到大取值时对应的一列函数值,因此在研究某些数列问题时,利用函数思想既有利于理解问题的本质,又简化了运算,如求等差数列前n项和的最值时,构建二次函数则简洁明了,求数列的最大项或最小项,可以根据函数的单调性求出最值.
[典例13] 设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=21,S15=-75,Tn为数列的前n项和,求Tn的最大值.
2 化归、转化思想
等差数列、等比数列的计算,一般先求a1,公差d或公比q;遇到an与Sn的关系时,可以利用an=Sn-Sn-1(n≥2)都转化为an或Sn,再转化为等差数列或等比数列,利用等差或等比数列的通项公式求出.其中合理的转化是解题的关键.
[典例14] 设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(n=2,3,4,…),求数列{bn}的通项bn;
(3)求和:b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
3 整体思想
解决某些数列问题时,往往要将其中的某一局部结构视为一个整体,利用整体思想简化结构,从而简化数列的运算.
[典例15] 已知等差数列{an}的前四项之和为-4,最后四项之和为36,且所有项之和为36,求其项数.
4 分类讨论思想
数列中某些问题往往需利用分类讨论思想来解决,如等比数列的前n项和公式中,若公比q的取值未知,则需要对q=1与q≠1分类求解;由Sn求an时应分n=1和n≥2两种情况讨论;某些数列的前n项和也需要讨论,通过分类讨论可以将复杂问题简单化,解题时要注意分类讨论标准的确定,做到不重不漏.
[典例16] 已知等比数列{an}的各项均为正数,2a5,a4,4a6成等差数列,且满足a4=4a,数列{bn}的前n项和Sn=bn,n∈N*,且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=求数列{cn}的前n项和Pn;
(3)设dn=an,n∈N*,数列{dn}的前n项和为Tn,求证:Tn<.
5 由有限到无限的思想
数学归纳法的基本原理,即归纳原理(也称多米诺骨牌效应)通过研究有限来洞察无限,实现了由有限到无限的数学飞跃.
[典例17] 已知数列{an}满足a2=6,=(n∈N*).
(1)求a1,a3,a4,a5的值;
(2)猜想{an}的通项公式,并用数学归纳法证明.
知识系统整合
规律方法收藏
1.由数列的前n项和求an时,应注意是
an=若an=Sn-Sn-1(n≥2)对于n=1也成立,则合并写成一个an的式子,否则分段表示an.
2.使用an-an-1=d(常数)或=q(常数)证明等差或等比数列时,以上两式中均应注明(n≥2,n∈N*),否则,数列不是等差数列或等比数列.
3.牢记等差、等比数列的一些重要性质并应用,往往能迅速地解决问题,但是不要忘记解等差、等比数列问题常用的基本量法,才是通用方法.
4.使用等比数列前n项和公式时,应注意公比q是否等于1.
5.等差、等比数列的通项公式和前n项和公式是它们的重要基本公式,对这两个公式要用方程思想、函数思想并从变形与发展的角度去深刻认识.
6.解等差、等比数列的综合题必须牢固掌握基础知识、基本技能和基本题型,并且要灵活运用这些知识,善于将综合题分解为几个基本题.解等差、等比数列的应用题,关键是将抽象的文字语言转化为数学语言,应用数列的定义、公式及性质加以解决.这就要求能真正理解题意、理清其脉络,从纷繁复杂的实际问题中发掘出其本质特征.
7.应用数列知识解应用题,应首先读懂题意,然后建立数学模型,最后求解、回答.
8.判断数列{an}为等差数列的充要条件
(1)数列{an}是等差数列?an-an-1=d(n≥2).
(2)数列{an}是等差数列?2an=an+1+an-1(n≥2).
(3)数列{an}是等差数列?an=pn+q(p,q是与n无关的常数).
(4)数列{an}是等差数列?a1+a2+…+an=An2+Bn(A,B为常数).
9.等差数列与等比数列的转换
(1)若数列{an}是等差数列,则数列{aan}(a>0,a≠1)是等比数列.
(2)若数列{an}是等比数列,则数列{lg |an|}是等差数列.
10.数学归纳法的运用关键在于对归纳原理的深刻理解.
学科思想培优
一、数列通项公式的求法
数列的通项公式是数列的核心之一,它如同函数中的解析式一样,有解析式便可研究函数的性质,而有了数列的通项公式,便可求出数列中的任何一项及前n项和.常见的数列通项公式的求法有以下几种:
1 观察归纳法求数列的通项公式
就是观察数列的特征,横向看各项之间的关系结构,纵向看各项与序号n的内在联系,结合常见数列的通项公式,归纳出所求数列的通项公式.
2 利用公式法求数列的通项公式
数列符合等差数列或等比数列的定义,求通项时,只需求出a1与d或a1与q,再代入公式an=a1+(n-1)d或an=a1qn-1中即可.
3 利用an与Sn的关系求数列的通项公式
如果给出的条件是an与Sn的关系式,可利用an=先求出a1=S1,再通过计算求出an(n≥2)的关系式,检验当n=1时,a1是否满足该式,若不满足该式,则an要分段表示.
4 利用累加法、累乘法求数列的通项公式
形如:已知a1,且an+1-an=f(n)(f(n)是可求和数列)的形式均可用累加法;
形如:已知a1,且=f(n)(f(n)是可求积数列)的形式均可用累乘法.
5 构造法(利用数列的递推公式研究数列的通项公式)
若由已知条件直接求an较难,可以通过整理变形等,从中构造出一个等差数列或等比数列,从而求出通项公式.
[典例1] 数列{an}中,an+1=2an+1,且a1=1,求通项公式an.
[解] 解法一:(迭代法)
an=2an-1+1=2(2an-2+1)+1=22an-2+2×1+1=23an-3+22×1+2×1+1=…=2n-1a1+(2n-2+2n-3+…+2+1)=2n-1+2n-2+…+2+1=2n-1.
解法二:(待定系数法)
由an+1=2an+1,
设an+1+k=2(an+k),∴an+1=2an+k,∴k=1,
∴{an+1}为等比数列,∴a1+1=2,公比为2,
∴an+1=2×2n-1,∴an=2n-1.
解法三:(累加法)
由an+1=2an+1,an=2an-1+1,得
an+1-an=2(an-an-1)(n≥2).
故{an+1-an}是首项为a2-a1=2,公比为2的等比数列,即an+1-an=2·2n-1=2n,
利用累加得an=2n-1.
[典例2] 在数列{an}中,已知a1=2且an+1=4an-3n+1,求通项公式an.
[解] 令an+1-A(n+1)-B=4(an-An-B),
则an+1=4an-3An+A-3B.
由条件得解得
即an+1-(n+1)=4(an-n),故数列{an-n}是首项为a1-1=1,公比为4的等比数列,从而an-n=4n-1,故an=4n-1+n.
[典例3] 已知数列{an}满足an+1=2an+3×5n,a1=2,求数列{an}的通项公式.
[解] 两边同除以5n+1,得=×+,
可得-1=.
由于-1=-≠0,所以数列是以-为首项,为公比的等比数列,从而-1=-×n-1,故数列{an}的通项公式为an=5n-3×2n-1.
[典例4] 已知数列{an}中,a1=,an+1=,求数列{an}的通项公式.
[解] 由题意,可得==+2,
又=,所以数列是首项为,公差为2的等差数列,故=+2(n-1)=,
所以数列{an}的通项公式为an=.
[典例5] 设Sn为数列{an}的前n项的和,且Sn=(an-1)(n∈N*),求数列{an}的通项公式.
[解] ∵Sn=(an-1),
∴当n=1时,S1=a1=(a1-1),解得a1=3.
当n≥2时,an=Sn-Sn-1=(an-1)-(an-1-1),得=3,∴数列{an}是以3为公比的等比数列,且首项a1=3.故数列的通项公式为an=3n(n∈N*).
[典例6] 在数列{an}中,a1=2,an+1=an,求通项公式an.
[解] ∵a1=2,an+1=an,
∴=,=,…,=,
以上n-1个等式左右两边分别相乘得=n·2n-1,即an=n·2n,且n=1时,a1=2也适合上式,
∴an=n·2n.
二、以数阵为背景的数列问题
1 数阵的特点
所谓数阵是指将某些数,按一定的规律排成若干行和列,形成图表,也称之为数表,例如大家都非常熟悉的“杨辉三角”.数阵不仅有正方形、三角形,还有长方形、圆、多边形、星形、花瓣形、十字形,甚至几种图形的组合,变幻多样、对称性强,很能吸引人.在我们平常解题中最常见的是前两种.
2 以数阵为背景的数列问题
数阵中的数是按一定的规律排成若干行和列,比较多见的是排成等差或等比数列,它重点考查等差、等比数列的相关知识,有时也会出现其他类型的数列,解决此类问题的关键是找出其中的规律,这就要求考生要有较强的观察、归纳、猜想能力以及对数列知识的融合迁移能力,下面例谈一下它的几种题型.
题型一 求数阵所暗示的规律(即通项公式)
[典例7] 如下图的数阵,则第n行的数从左到右依次是__________.
[解析] 设第n行左边第一个数为an,则a1=1,a2=3=a1+2×1,a3=7=a2+2×2,…,an=an-1+2(n-1).叠加得an=n2-n+1,故第n行的数从左到右依次是n2-n+1,n2-n+3,n2-n+5,…,n2-n+(2n-1).
[答案] n2-n+1,n2-n+3,n2-n+5,…,n2-n+(2n-1)
[典例8] 把自然数1,2,3,4,…按下列方式排成一个数阵.
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … …
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
[解析] 该数阵的第1行有1个数,第2行有2个数,…,第n行有n个数,则第n-1(n≥3)行的最后一个数为=-,则第n行从左至右的第3个数为-+3.
[答案] -+3
题型二 求数阵中指定的某些项
[典例9] 在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,则标有*号的空格应填的数是__________.
*
74
2y
186
y
103
0 x 2x
[解析] 记aij为第i行第j列的格中所填的数,则a52=x,a41=y.
由第3行得a33=,由第3列得a33=2×103-2x,所以2x+y=113.①
由第1列得a21=3y,则由第2行得a23=2×74-3y,由第3列得a33+103=a23+2x,所以a23=3×103-4x.所以2×74-3y=3×103-4x,即4x-3y=161,②
解①②,得x=50,y=13.所以a15=2×186-a55=2×186-4x=172,a13=2a33-a53=112,a14==142,故标有*号的空格应填142.
[答案] 142
[典例10] 在右表所示的3×3正方形的9个空格中填入正整数,使得每一行都成等差数列,每一列都成等比数列,则标有*号的空格应填的数是________.
1
3
*
12
[解析] 设标有*号的空格应填a,根据中间空格列方程,得×2=2,解得a=4,故标有*号的空格应填4.
[答案] 4
题型三 求数阵中某指定项的位置
[典例11] 自然数按下图所示规律排列,问2020是第几行第几个数?
[解] 设2020在第m行,则m是满足>2020的最小正整数,解得m=64.经分析知第64行左边第一个数是2017,则2020-2017+1=4,故2020是第64行第4个数.
题型四 求数阵中所有项或某些指定项的和
[典例12] 给定81个数排成数阵如下图所示,若每一行,每一列都构成等差数列,且正中间一个数a55=5,则此数阵中所有数之和为__________.
[解析] S=(a11+a12+…+a19)+(a21+a22+…+a29)+…+(a91+a92+…+a99)=9(a15+a25+…+a95)=9×9×a55=405.故此数阵中所有数之和为405.
[答案] 405
三、数列中的数学思想与方法
1 函数与方程思想
由于数列可以看作定义域为正整数集或正整数集的有限子集的函数an=f(n),数列中的项是自变量从小到大取值时对应的一列函数值,因此在研究某些数列问题时,利用函数思想既有利于理解问题的本质,又简化了运算,如求等差数列前n项和的最值时,构建二次函数则简洁明了,求数列的最大项或最小项,可以根据函数的单调性求出最值.
[典例13] 设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=21,S15=-75,Tn为数列的前n项和,求Tn的最大值.
[解] 设等差数列{an}的公差为d,则
Sn=na1+d,因为S7=21,S15=-75,
所以
解得
所以Sn=9n-(n2-n)=10n-n2,
所以=10-n.
因为-=-1,=9,所以数列是首项为9,公差为-1的等差数列,所以Tn==-n2+n=-2+.
因为n∈N*,所以当n=9或10时,Tn有最大值为45.
2 化归、转化思想
等差数列、等比数列的计算,一般先求a1,公差d或公比q;遇到an与Sn的关系时,可以利用an=Sn-Sn-1(n≥2)都转化为an或Sn,再转化为等差数列或等比数列,利用等差或等比数列的通项公式求出.其中合理的转化是解题的关键.
[典例14] 设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(n=2,3,4,…),求数列{bn}的通项bn;
(3)求和:b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
[解] (1)证明:∵a1=S1=1,S2=1+a2,
∴a2=,=.
又3tSn-(2t+3)Sn-1=3t,①
∴3tSn-1-(2t+3)Sn-2=3t(n≥3),②
①-②,得3tan-(2t+3)an-1=0,
∴=(n=2,3,…),
∴数列{an}是一个首项为1,公比为的等比数列.
(2)由f(t)==+,得
bn=f=+bn-1.
∴数列{bn}是一个首项为1,公差为的等差数列.
∴bn=1+(n-1)=.
(3)由bn=,可知{b2n-1}和{b2n}是首项分别为1和,公差均为的等差数列,
于是b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1=b2(b1-b3)+b4(b3-b5)+b6(b5-b7)+…+b2n(b2n-1-b2n+1)=-(b2+b4+…+b2n)=-×n×=-(2n2+3n).
3 整体思想
解决某些数列问题时,往往要将其中的某一局部结构视为一个整体,利用整体思想简化结构,从而简化数列的运算.
[典例15] 已知等差数列{an}的前四项之和为-4,最后四项之和为36,且所有项之和为36,求其项数.
[解] 由题意,得
①+②,得a1+a2+a3+a4+an+an-1+an-2+an-3=32,
∴4(a1+an)=32,∴a1+an=8.
又Sn==×8=36,∴n=9,
即该数列的项数为9.
4 分类讨论思想
数列中某些问题往往需利用分类讨论思想来解决,如等比数列的前n项和公式中,若公比q的取值未知,则需要对q=1与q≠1分类求解;由Sn求an时应分n=1和n≥2两种情况讨论;某些数列的前n项和也需要讨论,通过分类讨论可以将复杂问题简单化,解题时要注意分类讨论标准的确定,做到不重不漏.
[典例16] 已知等比数列{an}的各项均为正数,2a5,a4,4a6成等差数列,且满足a4=4a,数列{bn}的前n项和Sn=bn,n∈N*,且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=求数列{cn}的前n项和Pn;
(3)设dn=an,n∈N*,数列{dn}的前n项和为Tn,求证:Tn<.
[解] (1)因为an>0,所以q>0.
?
解得
所以an=n,
当n≥2时,bn=Sn-Sn-1=bn-,即=,
所以数列是首项为1的常数列,=1.
所以bn=n.
(2)由(1)可得cn=
当n为偶数时,Pn=(b1+b3+…+bn-1)+(a2+a4+…+an)
=[1+3+…+(n-1)]+
=(1+n-1)+
=+-·n;
当n为奇数时,Pn=Pn-1+bn=+-·n-1+n
=+-·n-1.
(3)证明:因为dn=·
=-,
所以Tn=-+-+…+-=-<.
5 由有限到无限的思想
数学归纳法的基本原理,即归纳原理(也称多米诺骨牌效应)通过研究有限来洞察无限,实现了由有限到无限的数学飞跃.
[典例17] 已知数列{an}满足a2=6,=(n∈N*).
(1)求a1,a3,a4,a5的值;
(2)猜想{an}的通项公式,并用数学归纳法证明.
[解] (1)∵a2=6,=,
当n=1时,=1,∴a1=1,
当n=2时,=,∴a3=15,
当n=3时,=,∴a4=28,
当n=4时,=,∴a5=45.
(2)由(1)猜想an=n(2n-1),证明如下:
①当n=1时,a1=1成立;
②假设n=k时,猜想成立,即ak=k(2k-1),
则当n=k+1时,有=,
化简,得ak+1=(k+1)(2k+1),
即当n=k+1时,猜想成立.
由①②可知,猜想对任意n∈N*都成立.
