人教版七年级数学下册5.3.1 平行线的性质导学课件(23张ppt)
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线的性质导学课件(23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 18:19:51 | ||
图片预览






文档简介
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
学习
目标
1.探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言.
2.会用平行线的性质进行简单的计算和推理.
1.平行线的性质1
两条平行直线被第三条直线所截,同位角________, 简称为:两直线________,同位角________.
相等
平行
相等
2.平行线的性质2
两条平行直线被第三条直线所截,内错角________, 简称为:两直线________,内错角________.
3.平行线的性质3
两条平行直线被第三条直线所截,同旁内角________, 简称为:两直线________,同旁内角________.
相等
平行
相等
互补
平行
互补
1.如果把“同位角相等,两直线平行”称为平行线的判定定理1,那么平行线的判定定理1与平行线的性质1是什么关系?
【答案】平行线的判定定理1与平行线的性质1都是表示两条平行直线与同位角之间的关系的,其主要区别是:平行线的判定定理1中,已知条件是同位角相等,由此得到两条直线平行;而平行线的性质1中,已知条件是两条直线平行,由此得到同位角相等.
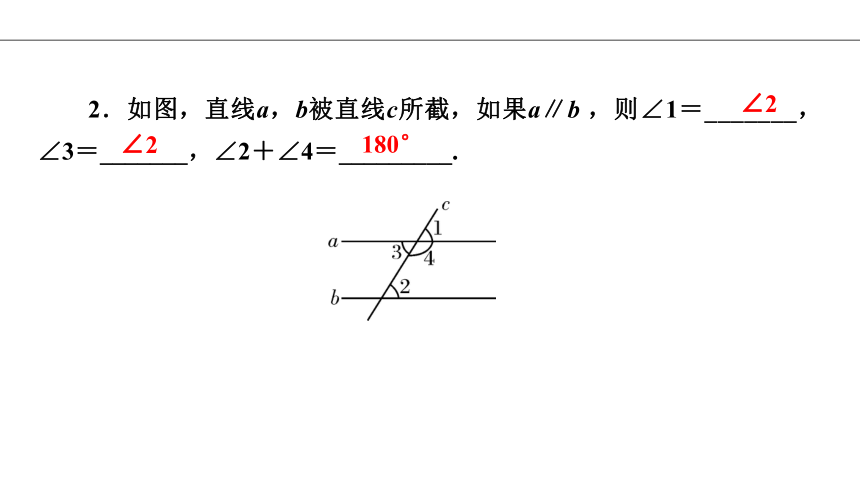
2.如图,直线a,b被直线c所截,如果a∥b ,则∠1=_______,∠3=_______,∠2+∠4=_________.
∠2
∠2
180°
知识点1 平行线的性质1
【例1】 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BEF的度数为 ( )
A.35°
B.60°
C.70°
D.80°
C
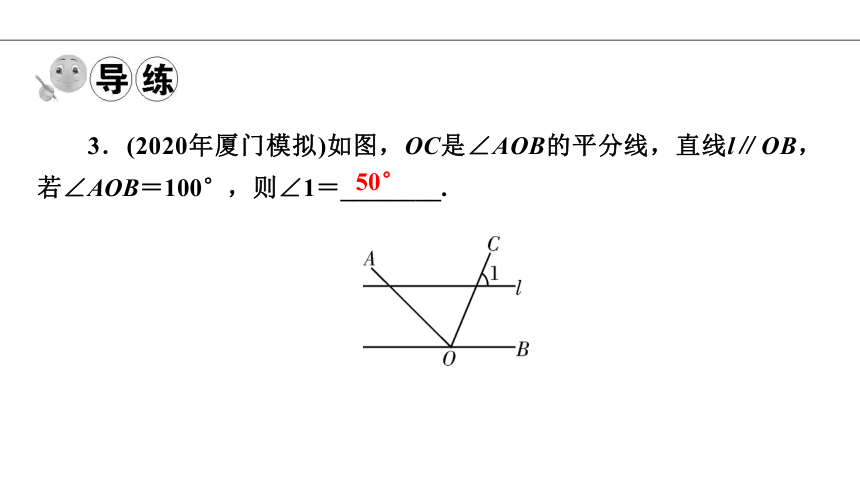
3.(2020年厦门模拟)如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=________.
50°
知识点2 平行线的性质2
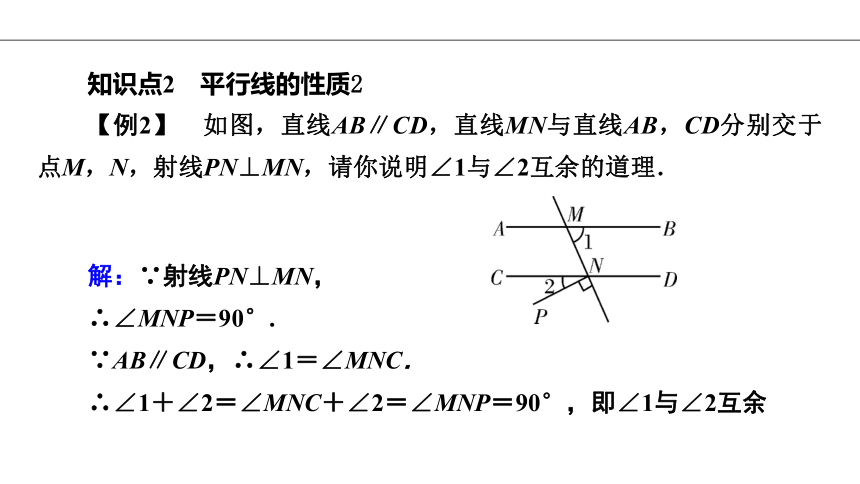
【例2】 如图,直线AB∥CD,直线MN与直线AB,CD分别交于点M,N,射线PN⊥MN,请你说明∠1与∠2互余的道理.
解:∵射线PN⊥MN,
∴∠MNP=90°.
∵AB∥CD,∴∠1=∠MNC.
∴∠1+∠2=∠MNC+∠2=∠MNP=90°,即∠1与∠2互余
4.(2020年武汉东西湖区期末)如图,直线AB,CD相交于点O,且OE为∠BOC的平分线,DF∥OE,若∠AOC=36°,求∠D的度数.
解:∵∠AOC=36°,∠AOC=∠BOD,
∴∠BOC=180°-∠AOC=144°,
∠BOD=36°.∵OE为∠BOC的平分线,∴∠BOE=72°.
∴∠EOD=∠BOD+∠BOE=36°+72°=108°.∵DF∥OE,∴∠D=∠EOD=108°.
知识点3 平行线的性质3
【例3】 如图,点A,C为∠FBE边上的两点,AD∥BE,AC平分∠BAD,若∠FAD=45°,求∠ACE的度数.
5.如图,四边形ABCD中,AB∥CD,AD∥BC,试说明∠A=∠C,∠B=∠D.
解:∵AD∥BC,
∴∠A+∠B=180°(两直线平行,同旁内角互补).
又∵AB∥CD,
∴∠B+∠C=180°(两直线平行,同旁内角互补).
∴∠A=∠C,同理∠B=∠D.
方法点拨:平行线的性质主要用于在平行线中进行角的计算,基本方法为:先看所求的角与已知角是否为同位角(或内错角、同旁内角),然后再找到与上述各角有关的平行线,进而利用平行线的性质即可进行角的计算.
【第一关】 建议用时3分钟
1.(2020年北京昌平区期末)如图,直线l与直线a,b分别相交,且a∥b,∠1=110°,则∠2的度数是 ( )
A.20°
B.70°
C.90°
D.110°
B
2.(2020年绍兴新昌县期末)如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠AEF=50°,则∠EFD的大小是 ( )
A.40°
B.50°
C.120°
D.130°
B
3.(2020年广州天河区模拟)如图,四边形ABCD中,AB∥CD,∠B=60°,则∠C=_________.
120°
?
【第二关】 建议用时6分钟
4.(2020年北京丰台区期末)如图,由AB∥DC可以得到 ( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.∠2=∠4
D
5.(2020年厦门模拟)如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=________.
50°
6.(2020年汕头期中)如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求∠C的度数.
解:∵∠1=∠D=68°,
∴AB∥CD.
∵∠2=50°,
∴∠AED=∠2=50°.
∵AE∥BC,
∴∠C=∠AED=50°.
【第三关】 自主选做
7.(2020年新疆天山区期末)按要求完成下列解题过程:
如图,AB∥CD,CB∥DE,说明∠B+∠D=180°.
解:∵AB∥CD,
∴∠B=________(__________________________).
∵CB∥DE,
∴∠C+________=180°(____________________________).
∴∠B+∠D=180°.
∠C
两直线平行,内错角相等
∠D
两直线平行,同旁内角互补
5.3 平行线的性质
5.3.1 平行线的性质
学习
目标
1.探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言.
2.会用平行线的性质进行简单的计算和推理.
1.平行线的性质1
两条平行直线被第三条直线所截,同位角________, 简称为:两直线________,同位角________.
相等
平行
相等
2.平行线的性质2
两条平行直线被第三条直线所截,内错角________, 简称为:两直线________,内错角________.
3.平行线的性质3
两条平行直线被第三条直线所截,同旁内角________, 简称为:两直线________,同旁内角________.
相等
平行
相等
互补
平行
互补
1.如果把“同位角相等,两直线平行”称为平行线的判定定理1,那么平行线的判定定理1与平行线的性质1是什么关系?
【答案】平行线的判定定理1与平行线的性质1都是表示两条平行直线与同位角之间的关系的,其主要区别是:平行线的判定定理1中,已知条件是同位角相等,由此得到两条直线平行;而平行线的性质1中,已知条件是两条直线平行,由此得到同位角相等.
2.如图,直线a,b被直线c所截,如果a∥b ,则∠1=_______,∠3=_______,∠2+∠4=_________.
∠2
∠2
180°
知识点1 平行线的性质1
【例1】 如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=35°,则∠BEF的度数为 ( )
A.35°
B.60°
C.70°
D.80°
C
3.(2020年厦门模拟)如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=________.
50°
知识点2 平行线的性质2
【例2】 如图,直线AB∥CD,直线MN与直线AB,CD分别交于点M,N,射线PN⊥MN,请你说明∠1与∠2互余的道理.
解:∵射线PN⊥MN,
∴∠MNP=90°.
∵AB∥CD,∴∠1=∠MNC.
∴∠1+∠2=∠MNC+∠2=∠MNP=90°,即∠1与∠2互余
4.(2020年武汉东西湖区期末)如图,直线AB,CD相交于点O,且OE为∠BOC的平分线,DF∥OE,若∠AOC=36°,求∠D的度数.
解:∵∠AOC=36°,∠AOC=∠BOD,
∴∠BOC=180°-∠AOC=144°,
∠BOD=36°.∵OE为∠BOC的平分线,∴∠BOE=72°.
∴∠EOD=∠BOD+∠BOE=36°+72°=108°.∵DF∥OE,∴∠D=∠EOD=108°.
知识点3 平行线的性质3
【例3】 如图,点A,C为∠FBE边上的两点,AD∥BE,AC平分∠BAD,若∠FAD=45°,求∠ACE的度数.
5.如图,四边形ABCD中,AB∥CD,AD∥BC,试说明∠A=∠C,∠B=∠D.
解:∵AD∥BC,
∴∠A+∠B=180°(两直线平行,同旁内角互补).
又∵AB∥CD,
∴∠B+∠C=180°(两直线平行,同旁内角互补).
∴∠A=∠C,同理∠B=∠D.
方法点拨:平行线的性质主要用于在平行线中进行角的计算,基本方法为:先看所求的角与已知角是否为同位角(或内错角、同旁内角),然后再找到与上述各角有关的平行线,进而利用平行线的性质即可进行角的计算.
【第一关】 建议用时3分钟
1.(2020年北京昌平区期末)如图,直线l与直线a,b分别相交,且a∥b,∠1=110°,则∠2的度数是 ( )
A.20°
B.70°
C.90°
D.110°
B
2.(2020年绍兴新昌县期末)如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠AEF=50°,则∠EFD的大小是 ( )
A.40°
B.50°
C.120°
D.130°
B
3.(2020年广州天河区模拟)如图,四边形ABCD中,AB∥CD,∠B=60°,则∠C=_________.
120°
?
【第二关】 建议用时6分钟
4.(2020年北京丰台区期末)如图,由AB∥DC可以得到 ( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.∠2=∠4
D
5.(2020年厦门模拟)如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=________.
50°
6.(2020年汕头期中)如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求∠C的度数.
解:∵∠1=∠D=68°,
∴AB∥CD.
∵∠2=50°,
∴∠AED=∠2=50°.
∵AE∥BC,
∴∠C=∠AED=50°.
【第三关】 自主选做
7.(2020年新疆天山区期末)按要求完成下列解题过程:
如图,AB∥CD,CB∥DE,说明∠B+∠D=180°.
解:∵AB∥CD,
∴∠B=________(__________________________).
∵CB∥DE,
∴∠C+________=180°(____________________________).
∴∠B+∠D=180°.
∠C
两直线平行,内错角相等
∠D
两直线平行,同旁内角互补
