2020-2021 学年八年级数学人教版下册 17.1.1 勾股定理 课件(42张)
文档属性
| 名称 | 2020-2021 学年八年级数学人教版下册 17.1.1 勾股定理 课件(42张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 18:21:42 | ||
图片预览









文档简介
第十七章
17.1.1 勾股定理
人教版数学八年级下册
学习目标
1.经历探索及验证勾股定理的过程,体会数形结合的思想.
2.掌握勾股定理,并运用它解决简单的计算题.
3.了解利用拼图验证勾股定理的方法.
导入新知
同学们,如图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗?
勾股定理
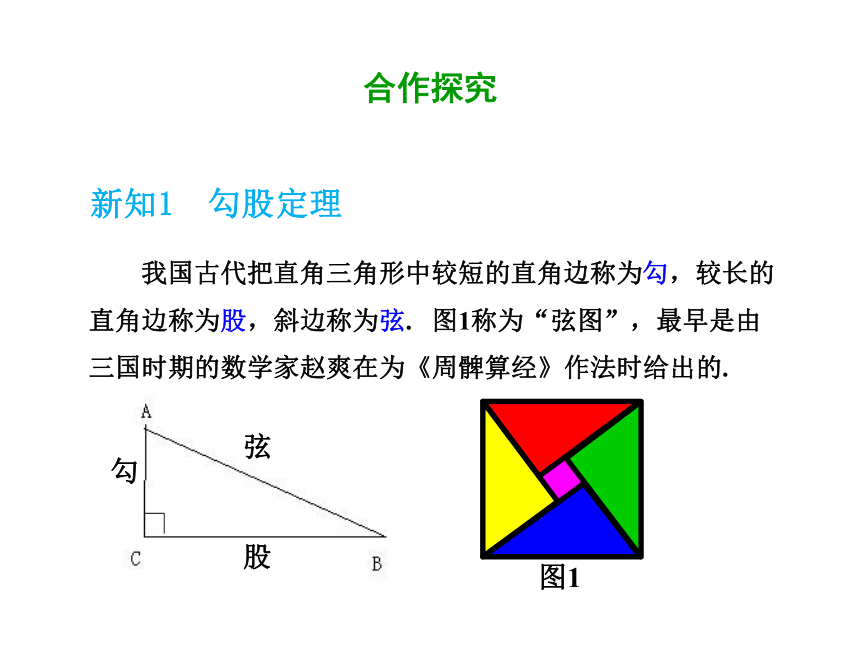
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1
新知1 勾股定理
合作探究
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(1)观察图2-1
正方形A中含有 个
小方格,即A的面积
是 个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形
=18(单位面积)
S正方形c
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
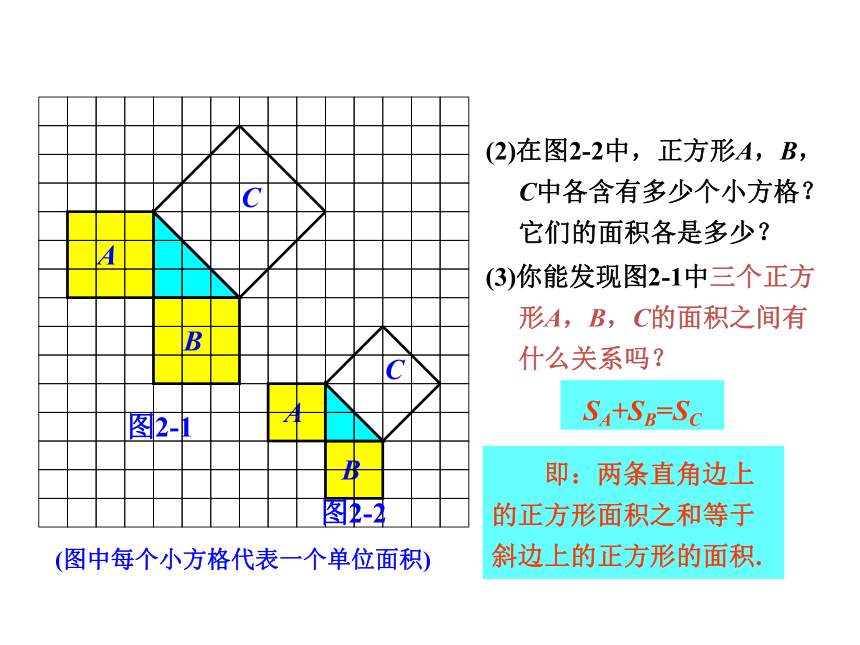
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积.
A
B
C
a
c
b
Sa+Sb=Sc
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
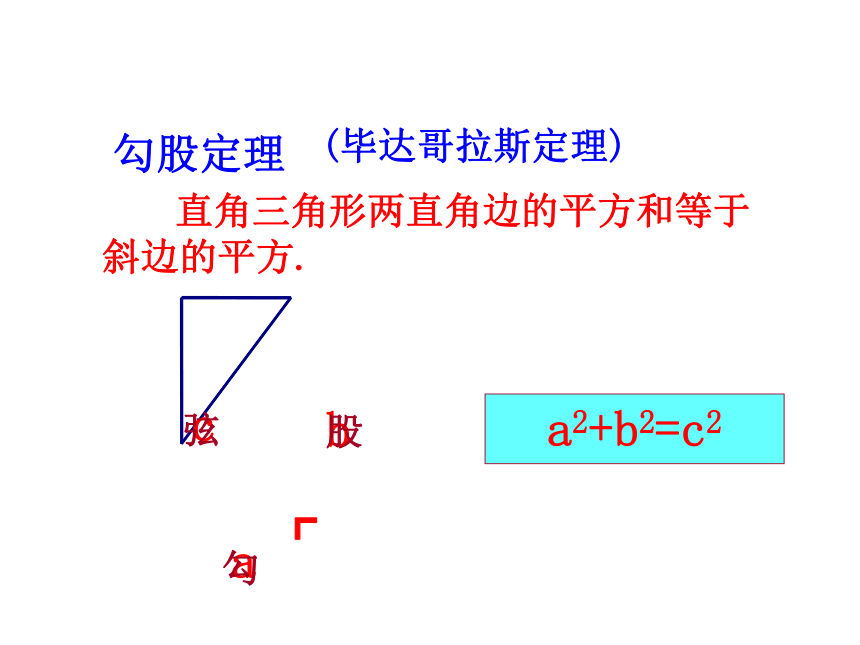
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
定义:直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
导引:
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
利用勾股定理求直角三角形的边长的方法:一般
都要经过“一分二代三化简”这“三步曲”,即一分:分
清哪条边是斜边,哪些是直角边;二代:将已知边长
及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
新知小结
1 设直角三角形的两条直角边长分别为a和b,斜边
长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
(1)
(2)
(3)
解:
巩固新知
下列说法中正确的是( )
A.已知a,b,c是三角形的三边长,则a2+b2=c2
B.在直角三角形中,两边的平方和等于第三边的
平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2
3 若一个直角三角形的两直角边的长分别为a,b,
斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
【中考·东营】在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等
于( )
A.10 B.8
C.6或10 D.8或10
C
4
【 中考·陕西】如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C. 若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A.3
B.6
C.3
D.
A
5
【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
C
6
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A.3
B.4
C.5
D.6
A
7
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
新知2 勾股定理与面积的关系
合作探究
例2 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积
为9,正方形Q的面积为
15,则正方形M的面积
为________;
(2)如图②,分别以直角
三角形ABC的三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是________;
(用图中字母表示)
(3)如图③,如果直角三角形两直角边的长分别为3和
4,分别以直角三角形的三边长为直径作半圆,请你
利用(2)中得出的结论求阴影部分的面积.
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
导引:
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
与直角三角形三边相连的正方形、半圆及正多边形、
圆都具有相同的结论:两直角边上图形面积的和等于斜
边上的图形面积.本例考查了勾股定理及正方形的面积
公式,半圆形面积的求法,解答此类题目的关键是仔细
观察所给图形,面积与边长、直径有平方关系,就很容
易联想到勾股定理.
新知小结
1 如图,直线l上有三个正方形a,b,c,若a,c的面
积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
D
巩固新知
如图,已知△ABC为直角三角形,分别以直角边AC,BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
2
C
【 中考·温州】四个全等的直角三角形按如图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( )
A.12S
B.10S
C.9S
D.8S
3
C
1. 勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
归纳新知
新知归纳
在△ABC中,边AB=15,AC=13,高AD=12,则
△ABC的周长是( )
A.42 B.32
C.42或32 D.不能确定
C
易错归纳
本题应分△ABC为锐角三角形和△ABC为钝角三角形两种情况讨论.解本题时常常容易忽略其中一种情况而出错.
易错点:考虑问题不全面而漏解.
两直角边的平方和
斜边的平方
a2+b2=c2
课后练习
A
A
C
【答案】D
面积
勾股定理
4
C
再 见
17.1.1 勾股定理
人教版数学八年级下册
学习目标
1.经历探索及验证勾股定理的过程,体会数形结合的思想.
2.掌握勾股定理,并运用它解决简单的计算题.
3.了解利用拼图验证勾股定理的方法.
导入新知
同学们,如图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗?
勾股定理
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1
新知1 勾股定理
合作探究
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(1)观察图2-1
正方形A中含有 个
小方格,即A的面积
是 个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形
=18(单位面积)
S正方形c
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积.
A
B
C
a
c
b
Sa+Sb=Sc
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
定义:直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
导引:
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
利用勾股定理求直角三角形的边长的方法:一般
都要经过“一分二代三化简”这“三步曲”,即一分:分
清哪条边是斜边,哪些是直角边;二代:将已知边长
及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
新知小结
1 设直角三角形的两条直角边长分别为a和b,斜边
长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
(1)
(2)
(3)
解:
巩固新知
下列说法中正确的是( )
A.已知a,b,c是三角形的三边长,则a2+b2=c2
B.在直角三角形中,两边的平方和等于第三边的
平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2
3 若一个直角三角形的两直角边的长分别为a,b,
斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
【中考·东营】在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等
于( )
A.10 B.8
C.6或10 D.8或10
C
4
【 中考·陕西】如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C. 若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A.3
B.6
C.3
D.
A
5
【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
C
6
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A.3
B.4
C.5
D.6
A
7
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
新知2 勾股定理与面积的关系
合作探究
例2 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积
为9,正方形Q的面积为
15,则正方形M的面积
为________;
(2)如图②,分别以直角
三角形ABC的三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是________;
(用图中字母表示)
(3)如图③,如果直角三角形两直角边的长分别为3和
4,分别以直角三角形的三边长为直径作半圆,请你
利用(2)中得出的结论求阴影部分的面积.
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
导引:
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
与直角三角形三边相连的正方形、半圆及正多边形、
圆都具有相同的结论:两直角边上图形面积的和等于斜
边上的图形面积.本例考查了勾股定理及正方形的面积
公式,半圆形面积的求法,解答此类题目的关键是仔细
观察所给图形,面积与边长、直径有平方关系,就很容
易联想到勾股定理.
新知小结
1 如图,直线l上有三个正方形a,b,c,若a,c的面
积分别为3和4,则b的面积为( )
A.3
B.4
C.5
D.7
D
巩固新知
如图,已知△ABC为直角三角形,分别以直角边AC,BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
2
C
【 中考·温州】四个全等的直角三角形按如图所示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为( )
A.12S
B.10S
C.9S
D.8S
3
C
1. 勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
归纳新知
新知归纳
在△ABC中,边AB=15,AC=13,高AD=12,则
△ABC的周长是( )
A.42 B.32
C.42或32 D.不能确定
C
易错归纳
本题应分△ABC为锐角三角形和△ABC为钝角三角形两种情况讨论.解本题时常常容易忽略其中一种情况而出错.
易错点:考虑问题不全面而漏解.
两直角边的平方和
斜边的平方
a2+b2=c2
课后练习
A
A
C
【答案】D
面积
勾股定理
4
C
再 见
