人教版八下数学达标练习19.1函数(word版含答案)
文档属性
| 名称 | 人教版八下数学达标练习19.1函数(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览


文档简介
人教版八下数学第十九章19.1函数
一、选择题
汽车以
千米/时的速度行驶,它驶过的路程
(千米)和所用时间
(时)的关系式是
,在这个变化过程中,常量与变量分别是
A.常量是
,变量是
B.常量是
,,变量是
C.常量是
,变量是
,
D.常量是
,,变量是
如果每盒铅笔
支,售价
元,那么铅笔的售价
(元)与铅笔的支数
(支)之间的关系式是
A.
B.
C.
D.
小刚以
米/分的速度匀速骑车
分钟,在原地休息了
分钟,然后以
米/分的速度骑回出发地.下列函数图象能表达这一过程的是
A.
B.
C.
D.
小亮家与姥姥家相距
,小亮
从家出发,骑自行车去姥姥家.妈妈
从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程
与北京时间
的函数图象如图所示.根据图象得到的结论,其中错误的是
A.小亮骑自行车的平均速度是
B.妈妈比小亮提前
小时到达姥姥家
C.妈妈在距家
处追上小亮
D.
妈妈追上小亮
小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华爷爷离家的距离
与时间
的函数关系的大致图象是
A.
B.
C.
D.
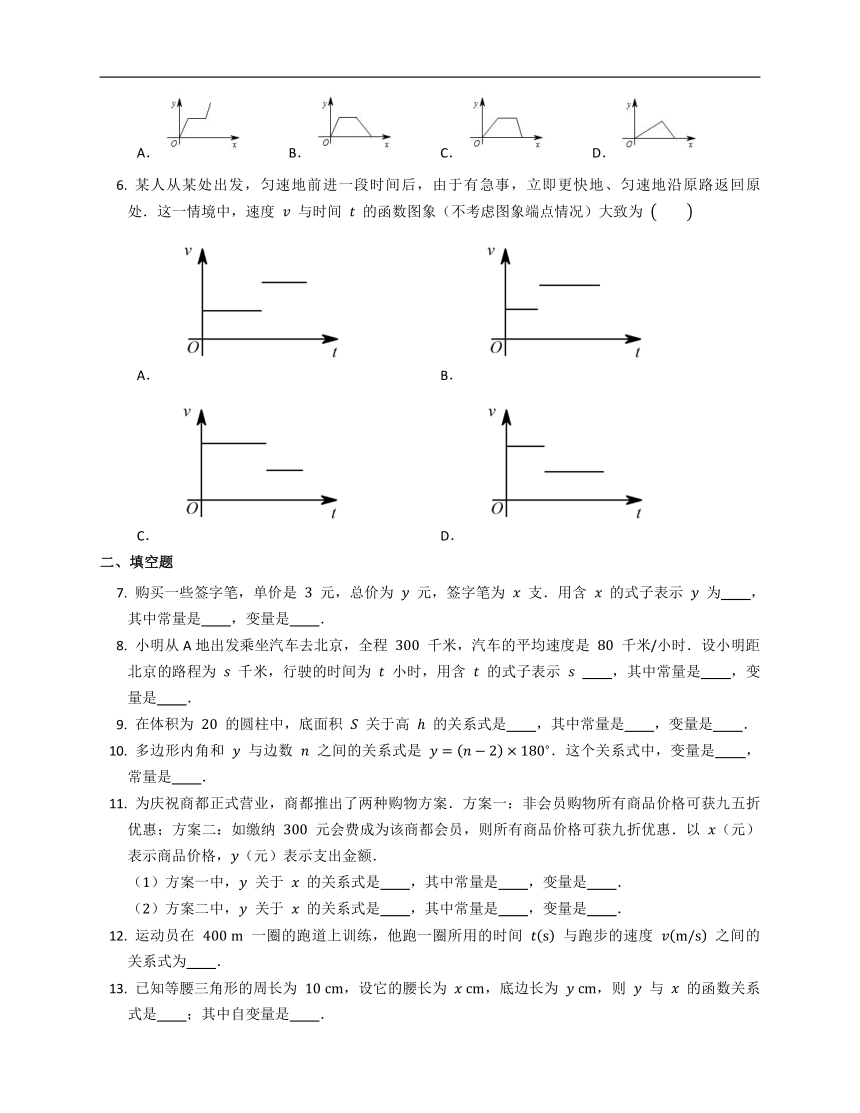
某人从某处出发,匀速地前进一段时间后,由于有急事,立即更快地、匀速地沿原路返回原处.这一情境中,速度
与时间
的函数图象(不考虑图象端点情况)大致为
A.
B.
C.
D.
二、填空题
购买一些签字笔,单价是
元,总价为
元,签字笔为
支.用含
的式子表示
为
,其中常量是
,变量是
.
小明从A地出发乘坐汽车去北京,全程
千米,汽车的平均速度是
千米/小时.设小明距北京的路程为
千米,行驶的时间为
小时,用含
的式子表示
,其中常量是
,变量是
.
在体积为
的圆柱中,底面积
关于高
的关系式是
,其中常量是
,变量是
.
多边形内角和
与边数
之间的关系式是
.这个关系式中,变量是
,常量是
.
为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠;方案二:如缴纳
元会费成为该商都会员,则所有商品价格可获九折优惠.以
(元)表示商品价格,(元)表示支出金额.
()方案一中,
关于
的关系式是
,其中常量是
,变量是
.
()方案二中,
关于
的关系式是
,其中常量是
,变量是
.
运动员在
一圈的跑道上训练,他跑一圈所用的时间
与跑步的速度
之间的关系式为
.
已知等腰三角形的周长为
,设它的腰长为
,底边长为
,则
与
的函数关系式是
;其中自变量是
.
张老师带领
名学生到某动物园参观,已知成人票每张
元,学生票每张
元,设门票的总费用为
元,则
,其中自变量是
,自变量的函数是
.
甲、乙两人在一次赛跑中,路程
与时间
的关系如图所示,请根据图象回答问题:
(1)这是一次
米赛跑;
(2)甲、乙两人中先到达终点的是
;
(3)甲速度是
米/秒.
小明从家跑步到学校,接着马上沿原路步行回家.如图是小明离家的路程
(米)与时间
(分)的函数图象,则小明回家的速度是每分钟步行
米;当
时,
随
的增大而
,当
时,
随
的增大而减小.
当
时,函数
与
的函数值相等,则
.
已知点
在函数
的图象上,则
的值为
.
三、解答题
周长为
的矩形,若它的一边是
,面积是
.
(1)
请用含
的式子表示
,并指出常量与变量;
(2)
当
时,求
的值.
已知函数
.
(1)
当
时对应的函数值是多少?
(2)
当
为何值时,函数值为
?
一个蓄水池有
的水,用每分钟抽水量为
的水泵抽水.
(1)
求蓄水池的余量
与抽水时间
(分)之间的函数关系式;
(2)
求自变量
的取值范围;
(3)
抽水
分钟后蓄水池中还有多少水?
(4)
几分钟后,蓄水池中还有水
?
小强骑自行车去郊游,下图是表示他离家的距离
(千米)与所用的时间
(小时)之间关系的函数图象.小强
点离家,
点回到家,根据这个图象,请你回答下列问题:
(1)
小强到离家最远的地方需要几小时?此时离家有多远?
(2)
何时开始第一次休息?休息多长时间?
(3)
小强在返程中的速度是多少?
学校为创建多媒体教学中心,备有资金
万元,已分批购进电脑
台,每台电脑单价
元.
(1)
求所剩资金
(万元)与电脑台数
(台)之间的函数解析式,并求出自变量的取值范围;
(2)
购入
台这种型号的电脑后还剩多少备用资金?
一个冷冻室开始的温度是
,开机降温后室温每小时下降
,设
表示开机降温工作
时的温度.
(1)
写出
与
之间的函数关系式;
(2)
说明经过几小时冷冻室温度降至
?何时降至
?
答案
一、选择题
1.
【答案】C
【知识点】常量、变量
2.
【答案】B
【知识点】解析式法
3.
【答案】C
【知识点】用函数图象表示实际问题中的函数关系
4.
【答案】D
【知识点】用函数图象表示实际问题中的函数关系
5.
【答案】C
【解析】此图象为三段,一是慢步到公园(
增大),二是在公园打太极拳(
不变),三是跑步回家(
减少).
【知识点】函数关系的表示
6.
【答案】A
【知识点】用函数图象表示实际问题中的函数关系
二、填空题
7.
【答案】
;
;
,
【知识点】解析式法
8.
【答案】
;
,
;
,
【知识点】解析式法、常量、变量
9.
【答案】
;
;
,
【知识点】解析式法
10.
【答案】
,
;
,
【知识点】常量、变量
11.
【答案】
;
;
,
;
;
,
;
,
【知识点】解析式法
12.
【答案】
【知识点】解析式法
13.
【答案】
;
【知识点】解析式法
14.
【答案】
;
;
【知识点】解析式法、自变量与函数值
15.
【答案】;乙;
【知识点】用函数图象表示实际问题中的函数关系
16.
【答案】;增大;
17.
【答案】
【知识点】自变量与函数值
18.
【答案】
【知识点】一次函数图像上点的坐标特征
三、解答题
19.
【答案】
(1)
,常量是
,变量是
和
.
(2)
【知识点】解析式法、自变量与函数值
20.
【答案】
(1)
(2)
【知识点】自变量与函数值
21.
【答案】
(1)
(2)
(3)
(4)
分钟
【知识点】函数自变量的取值范围、一次函数的解析式、一次函数的应用
22.
【答案】
(1)
小时;
千米.
(2)
在
时开始第一次休息;休息
小时.
(3)
千米/时.
【知识点】用函数图象表示实际问题中的函数关系
23.
【答案】
(1)
,自变量的取值范围是
,且
为整数.
(2)
还剩
万元.
【知识点】解析式法
24.
【答案】
(1)
.
(2)
小时;
小时.
【知识点】解析式法
一、选择题
汽车以
千米/时的速度行驶,它驶过的路程
(千米)和所用时间
(时)的关系式是
,在这个变化过程中,常量与变量分别是
A.常量是
,变量是
B.常量是
,,变量是
C.常量是
,变量是
,
D.常量是
,,变量是
如果每盒铅笔
支,售价
元,那么铅笔的售价
(元)与铅笔的支数
(支)之间的关系式是
A.
B.
C.
D.
小刚以
米/分的速度匀速骑车
分钟,在原地休息了
分钟,然后以
米/分的速度骑回出发地.下列函数图象能表达这一过程的是
A.
B.
C.
D.
小亮家与姥姥家相距
,小亮
从家出发,骑自行车去姥姥家.妈妈
从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程
与北京时间
的函数图象如图所示.根据图象得到的结论,其中错误的是
A.小亮骑自行车的平均速度是
B.妈妈比小亮提前
小时到达姥姥家
C.妈妈在距家
处追上小亮
D.
妈妈追上小亮
小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华爷爷离家的距离
与时间
的函数关系的大致图象是
A.
B.
C.
D.
某人从某处出发,匀速地前进一段时间后,由于有急事,立即更快地、匀速地沿原路返回原处.这一情境中,速度
与时间
的函数图象(不考虑图象端点情况)大致为
A.
B.
C.
D.
二、填空题
购买一些签字笔,单价是
元,总价为
元,签字笔为
支.用含
的式子表示
为
,其中常量是
,变量是
.
小明从A地出发乘坐汽车去北京,全程
千米,汽车的平均速度是
千米/小时.设小明距北京的路程为
千米,行驶的时间为
小时,用含
的式子表示
,其中常量是
,变量是
.
在体积为
的圆柱中,底面积
关于高
的关系式是
,其中常量是
,变量是
.
多边形内角和
与边数
之间的关系式是
.这个关系式中,变量是
,常量是
.
为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠;方案二:如缴纳
元会费成为该商都会员,则所有商品价格可获九折优惠.以
(元)表示商品价格,(元)表示支出金额.
()方案一中,
关于
的关系式是
,其中常量是
,变量是
.
()方案二中,
关于
的关系式是
,其中常量是
,变量是
.
运动员在
一圈的跑道上训练,他跑一圈所用的时间
与跑步的速度
之间的关系式为
.
已知等腰三角形的周长为
,设它的腰长为
,底边长为
,则
与
的函数关系式是
;其中自变量是
.
张老师带领
名学生到某动物园参观,已知成人票每张
元,学生票每张
元,设门票的总费用为
元,则
,其中自变量是
,自变量的函数是
.
甲、乙两人在一次赛跑中,路程
与时间
的关系如图所示,请根据图象回答问题:
(1)这是一次
米赛跑;
(2)甲、乙两人中先到达终点的是
;
(3)甲速度是
米/秒.
小明从家跑步到学校,接着马上沿原路步行回家.如图是小明离家的路程
(米)与时间
(分)的函数图象,则小明回家的速度是每分钟步行
米;当
时,
随
的增大而
,当
时,
随
的增大而减小.
当
时,函数
与
的函数值相等,则
.
已知点
在函数
的图象上,则
的值为
.
三、解答题
周长为
的矩形,若它的一边是
,面积是
.
(1)
请用含
的式子表示
,并指出常量与变量;
(2)
当
时,求
的值.
已知函数
.
(1)
当
时对应的函数值是多少?
(2)
当
为何值时,函数值为
?
一个蓄水池有
的水,用每分钟抽水量为
的水泵抽水.
(1)
求蓄水池的余量
与抽水时间
(分)之间的函数关系式;
(2)
求自变量
的取值范围;
(3)
抽水
分钟后蓄水池中还有多少水?
(4)
几分钟后,蓄水池中还有水
?
小强骑自行车去郊游,下图是表示他离家的距离
(千米)与所用的时间
(小时)之间关系的函数图象.小强
点离家,
点回到家,根据这个图象,请你回答下列问题:
(1)
小强到离家最远的地方需要几小时?此时离家有多远?
(2)
何时开始第一次休息?休息多长时间?
(3)
小强在返程中的速度是多少?
学校为创建多媒体教学中心,备有资金
万元,已分批购进电脑
台,每台电脑单价
元.
(1)
求所剩资金
(万元)与电脑台数
(台)之间的函数解析式,并求出自变量的取值范围;
(2)
购入
台这种型号的电脑后还剩多少备用资金?
一个冷冻室开始的温度是
,开机降温后室温每小时下降
,设
表示开机降温工作
时的温度.
(1)
写出
与
之间的函数关系式;
(2)
说明经过几小时冷冻室温度降至
?何时降至
?
答案
一、选择题
1.
【答案】C
【知识点】常量、变量
2.
【答案】B
【知识点】解析式法
3.
【答案】C
【知识点】用函数图象表示实际问题中的函数关系
4.
【答案】D
【知识点】用函数图象表示实际问题中的函数关系
5.
【答案】C
【解析】此图象为三段,一是慢步到公园(
增大),二是在公园打太极拳(
不变),三是跑步回家(
减少).
【知识点】函数关系的表示
6.
【答案】A
【知识点】用函数图象表示实际问题中的函数关系
二、填空题
7.
【答案】
;
;
,
【知识点】解析式法
8.
【答案】
;
,
;
,
【知识点】解析式法、常量、变量
9.
【答案】
;
;
,
【知识点】解析式法
10.
【答案】
,
;
,
【知识点】常量、变量
11.
【答案】
;
;
,
;
;
,
;
,
【知识点】解析式法
12.
【答案】
【知识点】解析式法
13.
【答案】
;
【知识点】解析式法
14.
【答案】
;
;
【知识点】解析式法、自变量与函数值
15.
【答案】;乙;
【知识点】用函数图象表示实际问题中的函数关系
16.
【答案】;增大;
17.
【答案】
【知识点】自变量与函数值
18.
【答案】
【知识点】一次函数图像上点的坐标特征
三、解答题
19.
【答案】
(1)
,常量是
,变量是
和
.
(2)
【知识点】解析式法、自变量与函数值
20.
【答案】
(1)
(2)
【知识点】自变量与函数值
21.
【答案】
(1)
(2)
(3)
(4)
分钟
【知识点】函数自变量的取值范围、一次函数的解析式、一次函数的应用
22.
【答案】
(1)
小时;
千米.
(2)
在
时开始第一次休息;休息
小时.
(3)
千米/时.
【知识点】用函数图象表示实际问题中的函数关系
23.
【答案】
(1)
,自变量的取值范围是
,且
为整数.
(2)
还剩
万元.
【知识点】解析式法
24.
【答案】
(1)
.
(2)
小时;
小时.
【知识点】解析式法
