2020-2021学年八年级数学人教版下册 第十八章 平行四边形 填空题专项培优提升练习(word版,含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 第十八章 平行四边形 填空题专项培优提升练习(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 21:02:00 | ||
图片预览


文档简介
人教版八年级下册 第十八章 平行四边形
填空题专项提升练习(二)
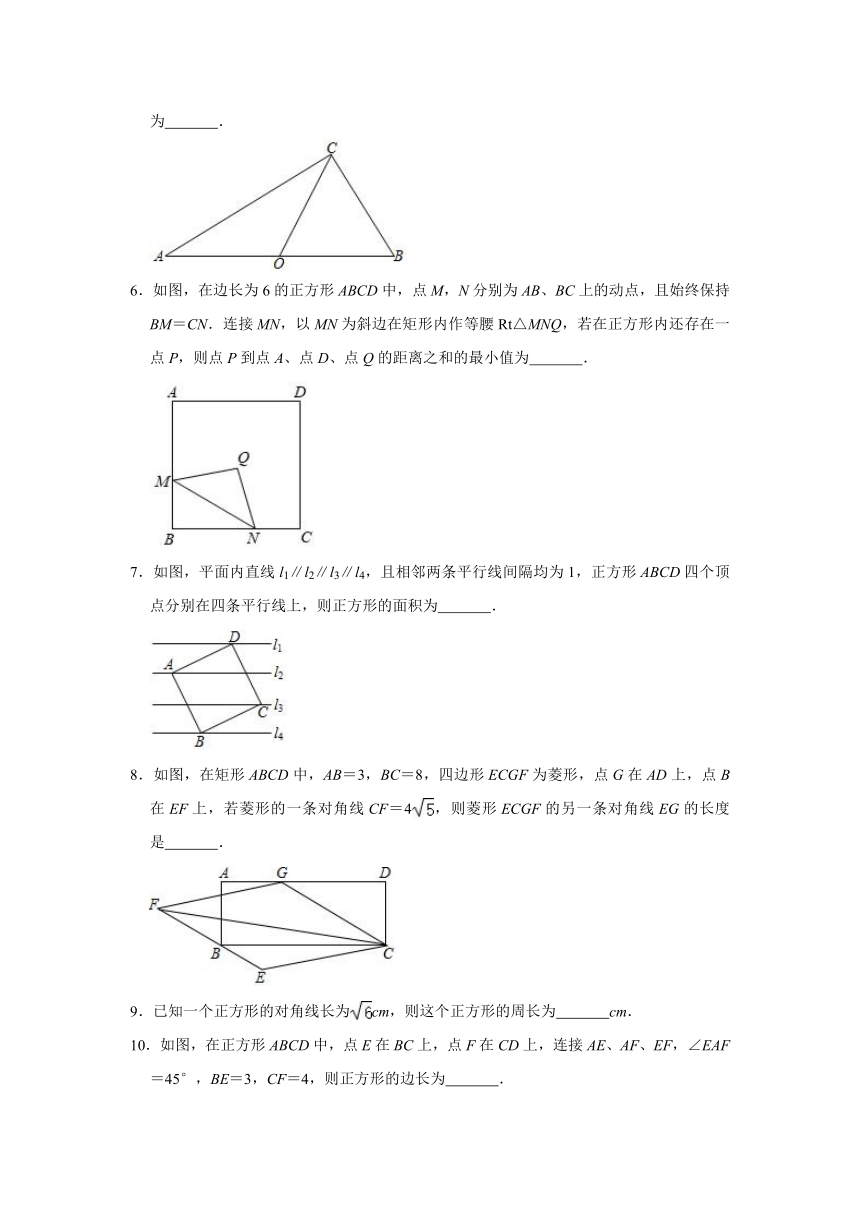
1.如图,正方形ABCD中,AB=3,点E为对角线AC上的动点,以DE为边作正方形DEFG.点H是CD上一点,且DH=CD,连接GH,则GH的最小值为 .
2.如图,点E,F分别在正方形ABCD的边AD,CD上,且AE=DF,连接BE,AF,BF,BE与AF相交于点G,点H,P分别为AB,BF的中点,连接GH,GP,若GH=4,GP=5,则EG的长为 .
3.如图,菱形ABCD和菱形CEFG中,∠ABC=60°,点B,C,E在同一条直线上,点D在CG上,BC=1,CE=3,H是AF的中点,则CH的长为 .
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且OE=2DE,则DE的长为 .
5.如图所示,△ABC中,O为AB边上的中点,OC=OB,若∠A=30°,则∠ACB的度数为 .
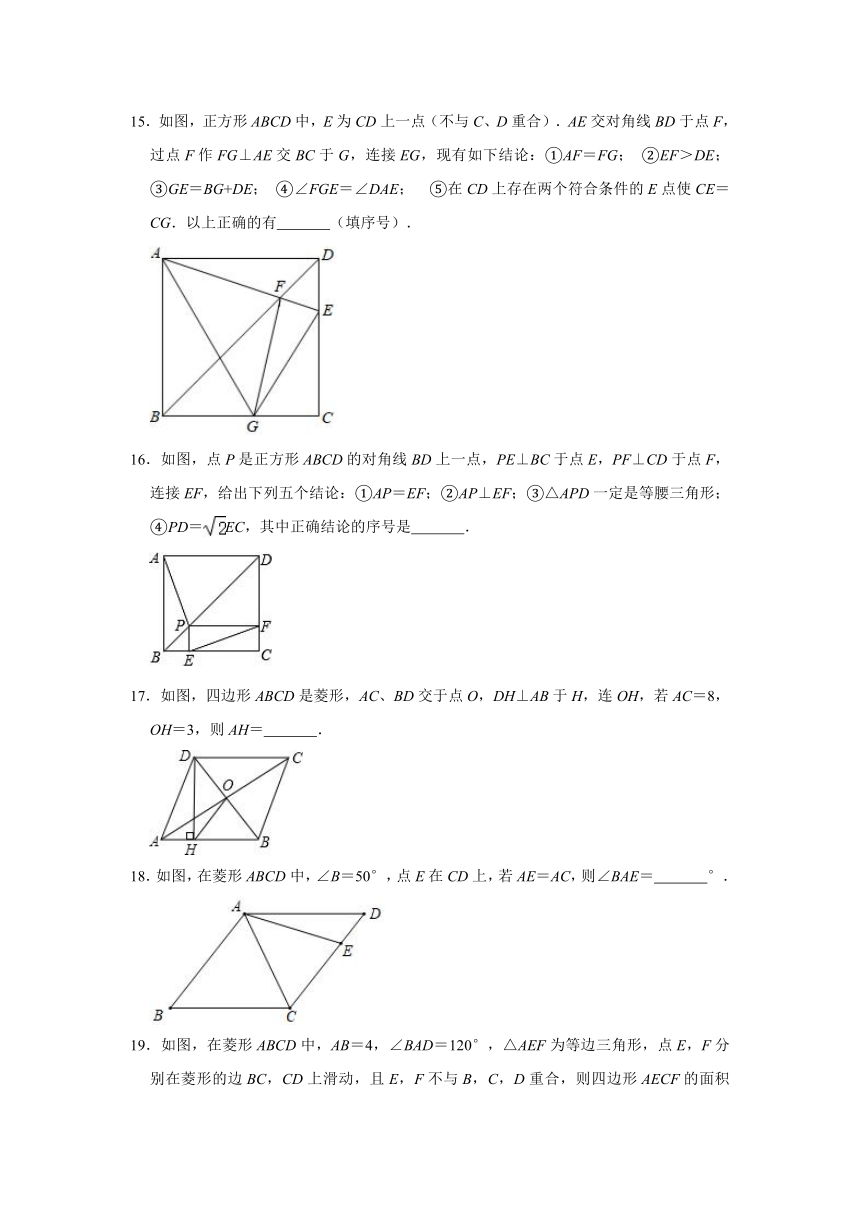
6.如图,在边长为6的正方形ABCD中,点M,N分别为AB、BC上的动点,且始终保持BM=CN.连接MN,以MN为斜边在矩形内作等腰Rt△MNQ,若在正方形内还存在一点P,则点P到点A、点D、点Q的距离之和的最小值为 .
7.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为 .
8.如图,在矩形ABCD中,AB=3,BC=8,四边形ECGF为菱形,点G在AD上,点B在EF上,若菱形的一条对角线CF=4,则菱形ECGF的另一条对角线EG的长度是 .
9.已知一个正方形的对角线长为cm,则这个正方形的周长为 cm.
10.如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .
11.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②△ABE≌△AHD;③BH=FH;④AB=HF;⑤BC﹣CF=2HE.其中正确的有
12.如图,正方形ABCD的边长为4,点E在CD边上,CE=3,若点F在正方形的某一边上,满足CF=BE,且CF与BE的交点为M,则CM= .
13.矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF交CD于点H,若AB=4,则BC﹣CH= .
14.如图,在长方形ABCD中,AB=6,AD=9,延长BC到E,使CE=3,连接DE.动点P从点B出发,以每秒3个单位的速度沿BC→CD→DA向终点A运动,设点P运动的时间为t秒,当t为 秒时,以P、A、B三点构成的三角形和△DCE全等.
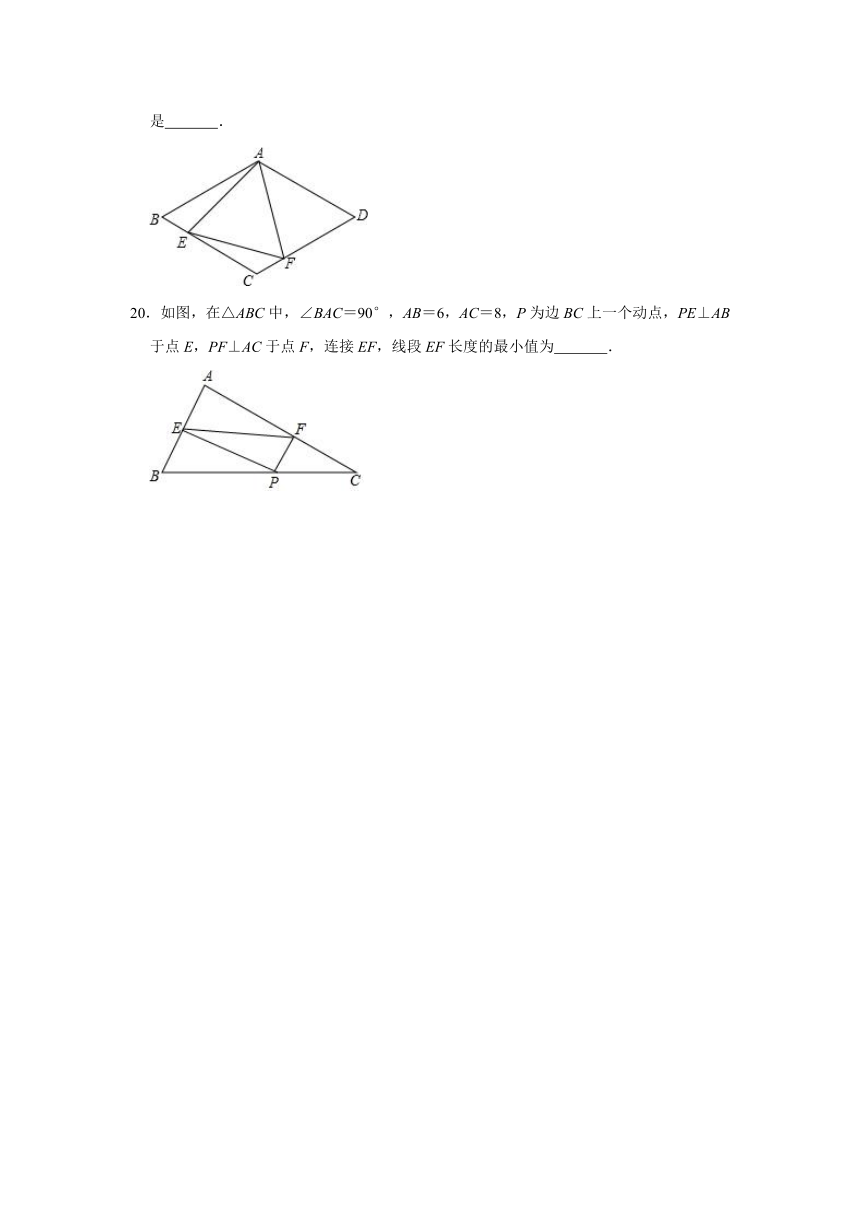
15.如图,正方形ABCD中,E为CD上一点(不与C、D重合).AE交对角线BD于点F,过点F作FG⊥AE交BC于G,连接EG,现有如下结论:①AF=FG; ②EF>DE;③GE=BG+DE; ④∠FGE=∠DAE; ⑤在CD上存在两个符合条件的E点使CE=CG.以上正确的有 (填序号).
16.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④PD=EC,其中正确结论的序号是 .
17.如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH= .
18.如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
19.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是 .
20.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一个动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,线段EF长度的最小值为 .
参考答案
1. .
2. .
3.解:如图,连接AC、CF,
∵菱形ABCD和菱形CEFG中,BC=1,CE=3,∠ABC=60°,
∴AC=BC=1,CF=3,
∠ACD=60°,∠GCF=30°,
∴∠ACF=90°,
由勾股定理得,AF==2,
∵H是AF的中点,
∴CH=AF=×2=.
故答案为:.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,BD=AC,OD=BD,OC=AC,
∴OC=OD,
∵EO=2DE,
∴设DE=m,OE=2m,
∴OD=OC=3m,
∵CE⊥BD,
∴∠DEC=∠OEC=90°,
在Rt△OCE中,∵OE2+CE2=OC2,
∴(2m)2+52=(3m)2,
解得:m=,
∴DE=;
故答案为.
5.解:∵O为AB边上的中点,OC=OB,
∴OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠A=30°,
∴∠A=∠ACO=30°,
∴∠COB=∠A+∠ACO=60°,
∴∠BCO=∠B=(180°﹣∠COB)=(180°﹣60°)=60°,
∴∠ACB=∠ACO+∠BCO)=30°+60°=90°,
故答案为:90°.
6. 3+3.
7.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
8. .
9.解:∵正方形的对角线长为cm
∴正方形的边长为:×sin45°=×=(cm),
∴正方形的周长为4(cm).
故答案为4.
10.解:延长CB至点G,使BG=DF,并连接AG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠DAF
∵∠EAF=45°,
∴∠BAE+∠DAF=∠BAE+∠GAB=∠GAE=45°,
∴∠EAF=∠GAE
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS)
∴GE=EF,
设正方形的边长为x,DF=x﹣4,EC=x﹣3,GE=EF=BG+BE=DF+BE=x﹣4+3=x﹣1,
在Rt△EFC中,EF2=EC2+CF2,
即(x﹣1)2=(x﹣3)2+42,
解得:x=6,
即正方形的边长为6,
故答案为:6.
11.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=AB,AD=AH,
∵AD=AB=AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
在△ABE和△AHD中,,
∴△ABE≌△AHD(AAS),故②正确;
∴BE=DH,
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°﹣67.5°=22.5°,
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,,
∴△BEH≌△HDF(ASA),
∴BH=HF,故③正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故④错误;
过H作HK⊥BC于K,
可知KC=BC,HK=KE,
由上知HE=EC,
∴BC=KE十EC,
又KE=HK=FC,HE=EC,
故BC=HK+HE,BC=2HK+2HE=FC+2HE
∴⑤正确;
故答案为:①②③⑤.
12.解:分两种情况:
①如图1所示,当点F在AD上时,
由CF=BE,CD=BC,∠BCE=∠CDF=90°可得,Rt△BCE≌Rt△CDF(HL),
∴∠DCF=∠CBE,
又∵∠BCF+∠DCF=90°,
∴∠BCF+∠CBE=90°,
∴∠BMC=90°,即CF⊥BE,
∵BC=4,CE=3,∠BCE=90°,
∴BE=5,
∴CM==;
②如图2所示,当点F在AB上时,
同理可得,Rt△BCF≌Rt△CBE(HL),
∴BF=CE,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
又∵∠BCE=90°,
∴四边形BCEF是矩形,
∴CM=BE=×5=.
故答案为:或.
13.解:如图,过F作MN∥DC交AD于M,交BC于N,
∵四边形ABCD是矩形,
∴DC⊥AD.
∴MF⊥AD.
∵AF平分∠BAD,
∴∠1=∠2.
∵DF⊥AF,
∴∠2+∠3=90°.
又∠1+∠2=90°.
∴∠2=∠3.
∴AF=DF.
∴点M是AD的中点.
∴FN为△BCH的中位线,
∴FN=HC,FM=2,FN=4﹣2,HC=8﹣4,
则BC﹣HC=8﹣8.
故答案是:8﹣8.
14.解:∵四边形ABCD是矩形,
∴AB=CD=4,AD=BC=9,CD⊥BC,
∴∠ABC=∠DCE=∠BAD=90°,
若△ABP与△DCE全等,
∴BP=CE=3或AP=CE=3,
当BP=CE=3时,则t=1秒,
当AP=CE=3时,则t=9+6+9﹣3=21,则t=7秒,
∴当t为1秒或7秒时,△ABP和△DCE全等.
故答案为:1或7.
15.解:如图①,连接CF,
在正方形ABCD中,AB=BC,∠ABF=∠CBF=45°,
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵FG⊥AE,
∴在四边形ABGF中,∠BAF+∠BGF=360°﹣90°﹣90°=180°,
又∵∠BGF+∠CGF=180°,
∴∠BAF=∠CGF,
∴∠CGF=∠BCF,
∴CF=FG,
∴AF=FG,故①正确;
∵∠DFE=∠ADF+∠DAE=45°+∠DAE>∠FDE,
∴DE>EF,故②错误;
如图②,把△ADE顺时针旋转90°得到△ABH,则AH=AE,BH=DE,∠BAH=∠DAE,
∵AF=FG,FG⊥AE,
∴△AFG是等腰直角三角形,
∴∠EAG=45°,
∴∠HAG=∠BAG+∠DAE=90°﹣45°=45°,
∴∠EAG=∠HAG,
在△AHG和△AEG中,
,
∴△AHG≌△AEG(SAS),
∴HG=EG,
∵HG=BH+BG=DE+BG=EG,故③正确;
∵AF=FG,AF⊥FG,
∴∠FAG=∠FGA=45°,
∵△AHG≌△AEG,
∴∠AGH=∠AGE=∠AGF+∠EGF=45°+∠FGE,
∵AD∥BC,
∴∠DAG=∠AGH,
∴∠DAG=∠AGE=45°+∠DAE,
∴∠DAE=∠FGE,故④正确;
∵在CD上存在1个符合条件的E点使CE=CG,
∴⑤错误,
故答案为①③④.
16.解:延长FP交AB于点N,延长AP交EF于点M.
∵四边形ABCD是正方形.
∴∠ABP=∠CBD
又∵NP⊥AB,PE⊥BC,
∴四边形BNPE是正方形,∠ANP=∠EPF,
∴NP=EP,
∴AN=PF
在△ANP与△FPE中,
∵,
∴△ANP≌△FPE(SAS),
∴AP=EF,(故①正确);
△APN与△FPM中,∠APN=∠FPM,∠NAP=∠PFM
∴∠PMF=∠ANP=90°
∴AP⊥EF,(故②正确);
∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=EC
故正确的是:①②④.
故答案为:①②④
17.解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=BD=OB,
∴BD=6,
∴BO=3,S菱形ABCD=×6×8=24,
∵AO=AC=4,
∴AB=5,
∴DH=,
∵AD=5,
∴AH==.
故答案为:.
18.解:∵四边形ABCD是菱形,
∴CA平分∠BCD,AB∥CD,
∴∠BAE+∠AEC=180°,∠B+∠BCD=180°,
∴∠BCD=180°﹣∠B=180°﹣50°=130°,
∴∠ACE=∠BCD=65°,
∵AE=AC,
∴∠AEC=∠ACE=65°,
∴∠BAE=180°﹣∠AEC=115°;
故答案为:115.
19.解:(1)连接AC,如图所示,
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BAC=∠DAC=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,BC∥AD,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC、△ACD为等边三角形,
∴∠4=60°,AC=AB,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC=BC?AH=BC?=4.
故答案为:4.
20.解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB于点E,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF=AP,
当AP⊥BC时,AP最小,
∵BC?AP=AB?AC,
∴AP===4.8,
∴EF的最小值为4.8;
故答案为:4.8.
填空题专项提升练习(二)
1.如图,正方形ABCD中,AB=3,点E为对角线AC上的动点,以DE为边作正方形DEFG.点H是CD上一点,且DH=CD,连接GH,则GH的最小值为 .
2.如图,点E,F分别在正方形ABCD的边AD,CD上,且AE=DF,连接BE,AF,BF,BE与AF相交于点G,点H,P分别为AB,BF的中点,连接GH,GP,若GH=4,GP=5,则EG的长为 .
3.如图,菱形ABCD和菱形CEFG中,∠ABC=60°,点B,C,E在同一条直线上,点D在CG上,BC=1,CE=3,H是AF的中点,则CH的长为 .
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且OE=2DE,则DE的长为 .
5.如图所示,△ABC中,O为AB边上的中点,OC=OB,若∠A=30°,则∠ACB的度数为 .
6.如图,在边长为6的正方形ABCD中,点M,N分别为AB、BC上的动点,且始终保持BM=CN.连接MN,以MN为斜边在矩形内作等腰Rt△MNQ,若在正方形内还存在一点P,则点P到点A、点D、点Q的距离之和的最小值为 .
7.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为 .
8.如图,在矩形ABCD中,AB=3,BC=8,四边形ECGF为菱形,点G在AD上,点B在EF上,若菱形的一条对角线CF=4,则菱形ECGF的另一条对角线EG的长度是 .
9.已知一个正方形的对角线长为cm,则这个正方形的周长为 cm.
10.如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .
11.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②△ABE≌△AHD;③BH=FH;④AB=HF;⑤BC﹣CF=2HE.其中正确的有
12.如图,正方形ABCD的边长为4,点E在CD边上,CE=3,若点F在正方形的某一边上,满足CF=BE,且CF与BE的交点为M,则CM= .
13.矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF交CD于点H,若AB=4,则BC﹣CH= .
14.如图,在长方形ABCD中,AB=6,AD=9,延长BC到E,使CE=3,连接DE.动点P从点B出发,以每秒3个单位的速度沿BC→CD→DA向终点A运动,设点P运动的时间为t秒,当t为 秒时,以P、A、B三点构成的三角形和△DCE全等.
15.如图,正方形ABCD中,E为CD上一点(不与C、D重合).AE交对角线BD于点F,过点F作FG⊥AE交BC于G,连接EG,现有如下结论:①AF=FG; ②EF>DE;③GE=BG+DE; ④∠FGE=∠DAE; ⑤在CD上存在两个符合条件的E点使CE=CG.以上正确的有 (填序号).
16.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④PD=EC,其中正确结论的序号是 .
17.如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH= .
18.如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
19.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是 .
20.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一个动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,线段EF长度的最小值为 .
参考答案
1. .
2. .
3.解:如图,连接AC、CF,
∵菱形ABCD和菱形CEFG中,BC=1,CE=3,∠ABC=60°,
∴AC=BC=1,CF=3,
∠ACD=60°,∠GCF=30°,
∴∠ACF=90°,
由勾股定理得,AF==2,
∵H是AF的中点,
∴CH=AF=×2=.
故答案为:.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,BD=AC,OD=BD,OC=AC,
∴OC=OD,
∵EO=2DE,
∴设DE=m,OE=2m,
∴OD=OC=3m,
∵CE⊥BD,
∴∠DEC=∠OEC=90°,
在Rt△OCE中,∵OE2+CE2=OC2,
∴(2m)2+52=(3m)2,
解得:m=,
∴DE=;
故答案为.
5.解:∵O为AB边上的中点,OC=OB,
∴OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠A=30°,
∴∠A=∠ACO=30°,
∴∠COB=∠A+∠ACO=60°,
∴∠BCO=∠B=(180°﹣∠COB)=(180°﹣60°)=60°,
∴∠ACB=∠ACO+∠BCO)=30°+60°=90°,
故答案为:90°.
6. 3+3.
7.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
8. .
9.解:∵正方形的对角线长为cm
∴正方形的边长为:×sin45°=×=(cm),
∴正方形的周长为4(cm).
故答案为4.
10.解:延长CB至点G,使BG=DF,并连接AG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠DAF
∵∠EAF=45°,
∴∠BAE+∠DAF=∠BAE+∠GAB=∠GAE=45°,
∴∠EAF=∠GAE
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS)
∴GE=EF,
设正方形的边长为x,DF=x﹣4,EC=x﹣3,GE=EF=BG+BE=DF+BE=x﹣4+3=x﹣1,
在Rt△EFC中,EF2=EC2+CF2,
即(x﹣1)2=(x﹣3)2+42,
解得:x=6,
即正方形的边长为6,
故答案为:6.
11.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=AB,AD=AH,
∵AD=AB=AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
在△ABE和△AHD中,,
∴△ABE≌△AHD(AAS),故②正确;
∴BE=DH,
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°﹣67.5°=22.5°,
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,,
∴△BEH≌△HDF(ASA),
∴BH=HF,故③正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故④错误;
过H作HK⊥BC于K,
可知KC=BC,HK=KE,
由上知HE=EC,
∴BC=KE十EC,
又KE=HK=FC,HE=EC,
故BC=HK+HE,BC=2HK+2HE=FC+2HE
∴⑤正确;
故答案为:①②③⑤.
12.解:分两种情况:
①如图1所示,当点F在AD上时,
由CF=BE,CD=BC,∠BCE=∠CDF=90°可得,Rt△BCE≌Rt△CDF(HL),
∴∠DCF=∠CBE,
又∵∠BCF+∠DCF=90°,
∴∠BCF+∠CBE=90°,
∴∠BMC=90°,即CF⊥BE,
∵BC=4,CE=3,∠BCE=90°,
∴BE=5,
∴CM==;
②如图2所示,当点F在AB上时,
同理可得,Rt△BCF≌Rt△CBE(HL),
∴BF=CE,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
又∵∠BCE=90°,
∴四边形BCEF是矩形,
∴CM=BE=×5=.
故答案为:或.
13.解:如图,过F作MN∥DC交AD于M,交BC于N,
∵四边形ABCD是矩形,
∴DC⊥AD.
∴MF⊥AD.
∵AF平分∠BAD,
∴∠1=∠2.
∵DF⊥AF,
∴∠2+∠3=90°.
又∠1+∠2=90°.
∴∠2=∠3.
∴AF=DF.
∴点M是AD的中点.
∴FN为△BCH的中位线,
∴FN=HC,FM=2,FN=4﹣2,HC=8﹣4,
则BC﹣HC=8﹣8.
故答案是:8﹣8.
14.解:∵四边形ABCD是矩形,
∴AB=CD=4,AD=BC=9,CD⊥BC,
∴∠ABC=∠DCE=∠BAD=90°,
若△ABP与△DCE全等,
∴BP=CE=3或AP=CE=3,
当BP=CE=3时,则t=1秒,
当AP=CE=3时,则t=9+6+9﹣3=21,则t=7秒,
∴当t为1秒或7秒时,△ABP和△DCE全等.
故答案为:1或7.
15.解:如图①,连接CF,
在正方形ABCD中,AB=BC,∠ABF=∠CBF=45°,
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵FG⊥AE,
∴在四边形ABGF中,∠BAF+∠BGF=360°﹣90°﹣90°=180°,
又∵∠BGF+∠CGF=180°,
∴∠BAF=∠CGF,
∴∠CGF=∠BCF,
∴CF=FG,
∴AF=FG,故①正确;
∵∠DFE=∠ADF+∠DAE=45°+∠DAE>∠FDE,
∴DE>EF,故②错误;
如图②,把△ADE顺时针旋转90°得到△ABH,则AH=AE,BH=DE,∠BAH=∠DAE,
∵AF=FG,FG⊥AE,
∴△AFG是等腰直角三角形,
∴∠EAG=45°,
∴∠HAG=∠BAG+∠DAE=90°﹣45°=45°,
∴∠EAG=∠HAG,
在△AHG和△AEG中,
,
∴△AHG≌△AEG(SAS),
∴HG=EG,
∵HG=BH+BG=DE+BG=EG,故③正确;
∵AF=FG,AF⊥FG,
∴∠FAG=∠FGA=45°,
∵△AHG≌△AEG,
∴∠AGH=∠AGE=∠AGF+∠EGF=45°+∠FGE,
∵AD∥BC,
∴∠DAG=∠AGH,
∴∠DAG=∠AGE=45°+∠DAE,
∴∠DAE=∠FGE,故④正确;
∵在CD上存在1个符合条件的E点使CE=CG,
∴⑤错误,
故答案为①③④.
16.解:延长FP交AB于点N,延长AP交EF于点M.
∵四边形ABCD是正方形.
∴∠ABP=∠CBD
又∵NP⊥AB,PE⊥BC,
∴四边形BNPE是正方形,∠ANP=∠EPF,
∴NP=EP,
∴AN=PF
在△ANP与△FPE中,
∵,
∴△ANP≌△FPE(SAS),
∴AP=EF,(故①正确);
△APN与△FPM中,∠APN=∠FPM,∠NAP=∠PFM
∴∠PMF=∠ANP=90°
∴AP⊥EF,(故②正确);
∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=EC
故正确的是:①②④.
故答案为:①②④
17.解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=BD=OB,
∴BD=6,
∴BO=3,S菱形ABCD=×6×8=24,
∵AO=AC=4,
∴AB=5,
∴DH=,
∵AD=5,
∴AH==.
故答案为:.
18.解:∵四边形ABCD是菱形,
∴CA平分∠BCD,AB∥CD,
∴∠BAE+∠AEC=180°,∠B+∠BCD=180°,
∴∠BCD=180°﹣∠B=180°﹣50°=130°,
∴∠ACE=∠BCD=65°,
∵AE=AC,
∴∠AEC=∠ACE=65°,
∴∠BAE=180°﹣∠AEC=115°;
故答案为:115.
19.解:(1)连接AC,如图所示,
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BAC=∠DAC=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,BC∥AD,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC、△ACD为等边三角形,
∴∠4=60°,AC=AB,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC=BC?AH=BC?=4.
故答案为:4.
20.解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB于点E,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF=AP,
当AP⊥BC时,AP最小,
∵BC?AP=AB?AC,
∴AP===4.8,
∴EF的最小值为4.8;
故答案为:4.8.
