10.1.3古典概型-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(46张PPT)
文档属性
| 名称 | 10.1.3古典概型-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 17:53:36 | ||
图片预览









文档简介
第十章 概率
10.1 随机事件与概率
10.1.3 古典概型
学习目标
素养要求
1.结合具体实例,理解古典概型
数学抽象
2.能计算古典概型中简单随机事件的概率
数学抽象、数学建模
| 自学导引 |
1.概率:对随机事件发生________的度量(数值)称为事件的概率,事件A的概率用P(A)表示.
2.试验具有如下共同特征:
有限性:样本空间的样本点只有______个;
等可能性:每个样本点发生的可能性______.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概型的定义
可能性
有限
相等
【提示】(1)不属于古典概型,因为在区间[0,10]上任取一个数,其试验结果有无限个,故其样本点有无限个,所以不是古典概型.
(2)不一定是古典概型,还必须满足每个样本点出现的可能性相等才是古典概型.
(1)“在区间[0,10]上任取一个数,这个数恰为5的概率是多少?”这个概率模型属于古典概型吗?
(2)若一次试验的结果所包含的样本点的个数为有限个,则该试验是古典概型吗?
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A
包含其中k个样本点,则定义事件A的概率P(A)=________,其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型的概率计算公式
【预习自测】判断下列命题是否正确.(对的画“√”,错的画“×”)
(1)任何一个事件都是一个样本点. ( )
(2)古典概型中每一个样本点出现的可能性相等. ( )
(3)古典概型中的任何两个样本点都是互斥的. ( )
【答案】(1)× (2)√ (3)√
【解析】(1)一个事件可能是一个样本点,也可能包含多个样本点.
(2)古典概型具有等可能性.
(3)古典概型中的任何两个样本点都不能同时发生,所以是互斥的.
| 课堂互动 |
一只口袋内装有5个大小相同的球,白球3个,黑球2个,从中一次摸出2个球.
(1)共有多少个样本点?
(2)“2个都是白球”包含几个样本点?
素养点睛:本题考查了数学抽象的核心素养.
题型1 样本点的列举
解:(1)(方法一)采用列举法.
分别记白球为1,2,3号,黑球为4,5号,则样本点如下:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个(其中(1,2)表示摸到1号,2号球).
(方法二)采用列表法.
设5个球的编号分别为a,b,c,d,e,其中a,b,c为白球,d,e为黑球.列表如下:
编号
a
b
c
d
e
a
—
(a,b)
(a,c)
(a,d)
(a,e)
b
(b,a)
—
(b,c)
(b,d)
(b,e)
c
(c,a)
(c,b)
—
(c,d)
(c,e)
d
(d,a)
(d,b)
(d,c)
—
(d,e)
e
(e,a)
(e,b)
(e,c)
(e,d)
—
由于每次取2个球,每次所取2个球不相同,而摸到(b,a)与(a,b)是相同的事件,故共有10个样本点.
(2)方法一中“2个都是白球”包括(1,2),(1,3),(2,3),共3个样本点,法二中“2个都是白球”包括(a,b),(b,c),(a,c),共3个样本点.
样本点的三种列举方法
(1)直接列举法:把试验的全部结果一一列举出来.此方法适合于较为简单的试验问题.
(2)列表法:将样本点用表格的方式表示出来,通过表格可以弄清样本点的总数,以及要求的事件所包含的样本点数.列表法适用于较简单的试验的题目,样本点较多的试验不适合用列表法.
(3)树状图法:树状图法是使用树状的图形把样本点列举出来的一种方法,树状图法便于分析样本点间的结构关系,对于较复杂的问题,可以作为一种分析问题的主要手段,适用于较复杂的试验的题目.
1.袋中有2个标号分别为1,2的白球和2个标号分别为3,4的黑球.这4个球除颜色、标号外完全相同,4个人按顺序依次从中摸出1个球,求样本点的个数.
解:4个人按顺序依次从袋中摸出1个球的所有可能结果用树状图表示如图所示:
共24个样本点.
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
素养点睛:本题考查了数学抽象和数学运算的核心素养.
题型2 古典概型的概率计算
2.从1,2,3,4,5这五个数字中任取三个不同的数字,求下列事件的概率:
(1)事件A={三个数字中不含1和5};
(2)事件B={三个数字中含1或5}.
解:这个试验的基本事件为:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),所以基本事件总数n=10.
题型3 较复杂的古典概型的概率计算
【答案】A
解:将A,B,C,D四位贵宾就座情况用下面图形表示出来:
如上图所示,本题中的等可能基本事件共有24个.
解决有序和无序问题应注意两点
(1)不放回抽样,既可看成是有序的,也可看成是无序的,不影响结果,但必须注意观察角度要一致.
(2)放回抽样,注意在连续抽取两次时因顺序不同所得到的样本点也不同,所以存在顺序.
(2020年攀枝花模拟)为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了n户家庭进行问卷调查.经调查发现,这些家庭的月收人在5 000元到8 000元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一、三、四小组的频率之比为1∶3∶6,且第四小组的频数为18.
规范解答——古典概型与统计的综合
(1)求n;
(2)求这n户家庭月收人的众数与中位数(结果精确到0.1);
(3)这n户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取6户家庭,并从这6户家庭中随机抽取2户家庭进行慰问,求这2户家庭月收入至多有一户超过6 000元的概率.
题后反思:概率问题常常与统计问题结合在一起考查,在此类问题中,概率与频率的区别并不是十分明显,通常直接用题目中的频率代替概率进行计算.解决与古典概型的交汇的问题,应明确相关事件,列举样本点,然后利用古典概型的概率计算公式求解.
| 素养达成 |
1.某校高一年级要组建数学、计算机、航空模型三个兴趣小组,某学生只选报其中的2个,则基本事件共有 ( )
A.1个 B.2个
C.3个 D.4个
【答案】C
【解析】该生选报的所有可能情况:{数学和计算机},{数学和航空模型},{计算机和航空模型},所以基本事件有3个.故选C.
2.下列试验中是古典概型的是 ( )
A.种下一粒花生,观察它是否发芽
B.向正方形ABCD内,任意投掷一点P,观察点P是否与正方形的中心O重合
C.从1,2,3,4四个数中,任取两个数,求所取两数之积是2的概率
D.在区间[0,5]内任取一点,求此点小于2的概率
【答案】C
【解析】A中花生发芽与不发芽的概率不一定相等,故不是古典概型,B,D中的试验中的基本事件有无数多个,不是古典概型;C中试验有6个基本事件,且每个基本事件发生的概率相同,是古典概型.故选C.
【答案】D
【答案】C
5.一个盒子内放有5个完全相同的小球,其上分别标有号码1,2,3,4,5.从中任取一个,记下号数后放回,再取出1个,记下号数后放回,按顺序记录为(x,y),试写出“所得两球的号数和为6”所包含的基本事件.
解:列表表示所有的基本事件.
由上表可直观地看出,“所得两球的号数和为
6”包含以下5个基本事件:(1,5),(2,4),(3,3),(4,
2),(5,1).
| 课后提能训练 |
10.1 随机事件与概率
10.1.3 古典概型
学习目标
素养要求
1.结合具体实例,理解古典概型
数学抽象
2.能计算古典概型中简单随机事件的概率
数学抽象、数学建模
| 自学导引 |
1.概率:对随机事件发生________的度量(数值)称为事件的概率,事件A的概率用P(A)表示.
2.试验具有如下共同特征:
有限性:样本空间的样本点只有______个;
等可能性:每个样本点发生的可能性______.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概型的定义
可能性
有限
相等
【提示】(1)不属于古典概型,因为在区间[0,10]上任取一个数,其试验结果有无限个,故其样本点有无限个,所以不是古典概型.
(2)不一定是古典概型,还必须满足每个样本点出现的可能性相等才是古典概型.
(1)“在区间[0,10]上任取一个数,这个数恰为5的概率是多少?”这个概率模型属于古典概型吗?
(2)若一次试验的结果所包含的样本点的个数为有限个,则该试验是古典概型吗?
一般地,设试验E是古典概型,样本空间Ω包含n个样本点,事件A
包含其中k个样本点,则定义事件A的概率P(A)=________,其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
古典概型的概率计算公式
【预习自测】判断下列命题是否正确.(对的画“√”,错的画“×”)
(1)任何一个事件都是一个样本点. ( )
(2)古典概型中每一个样本点出现的可能性相等. ( )
(3)古典概型中的任何两个样本点都是互斥的. ( )
【答案】(1)× (2)√ (3)√
【解析】(1)一个事件可能是一个样本点,也可能包含多个样本点.
(2)古典概型具有等可能性.
(3)古典概型中的任何两个样本点都不能同时发生,所以是互斥的.
| 课堂互动 |
一只口袋内装有5个大小相同的球,白球3个,黑球2个,从中一次摸出2个球.
(1)共有多少个样本点?
(2)“2个都是白球”包含几个样本点?
素养点睛:本题考查了数学抽象的核心素养.
题型1 样本点的列举
解:(1)(方法一)采用列举法.
分别记白球为1,2,3号,黑球为4,5号,则样本点如下:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个(其中(1,2)表示摸到1号,2号球).
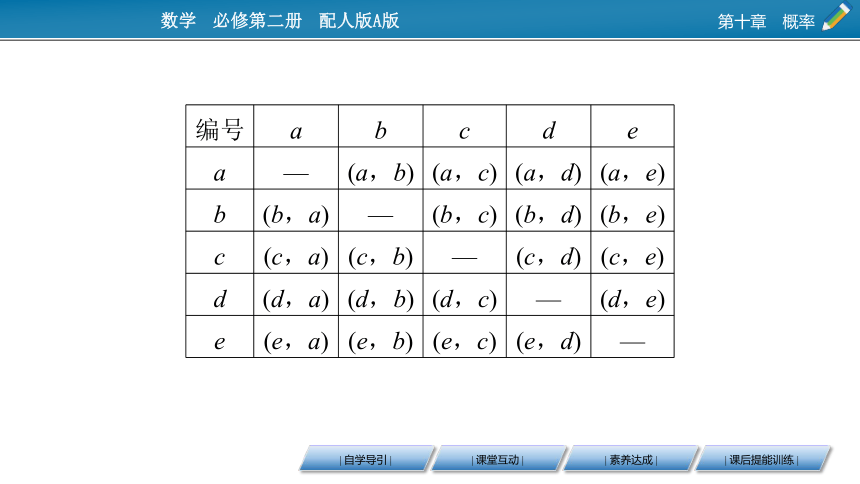
(方法二)采用列表法.
设5个球的编号分别为a,b,c,d,e,其中a,b,c为白球,d,e为黑球.列表如下:
编号
a
b
c
d
e
a
—
(a,b)
(a,c)
(a,d)
(a,e)
b
(b,a)
—
(b,c)
(b,d)
(b,e)
c
(c,a)
(c,b)
—
(c,d)
(c,e)
d
(d,a)
(d,b)
(d,c)
—
(d,e)
e
(e,a)
(e,b)
(e,c)
(e,d)
—
由于每次取2个球,每次所取2个球不相同,而摸到(b,a)与(a,b)是相同的事件,故共有10个样本点.
(2)方法一中“2个都是白球”包括(1,2),(1,3),(2,3),共3个样本点,法二中“2个都是白球”包括(a,b),(b,c),(a,c),共3个样本点.
样本点的三种列举方法
(1)直接列举法:把试验的全部结果一一列举出来.此方法适合于较为简单的试验问题.
(2)列表法:将样本点用表格的方式表示出来,通过表格可以弄清样本点的总数,以及要求的事件所包含的样本点数.列表法适用于较简单的试验的题目,样本点较多的试验不适合用列表法.
(3)树状图法:树状图法是使用树状的图形把样本点列举出来的一种方法,树状图法便于分析样本点间的结构关系,对于较复杂的问题,可以作为一种分析问题的主要手段,适用于较复杂的试验的题目.
1.袋中有2个标号分别为1,2的白球和2个标号分别为3,4的黑球.这4个球除颜色、标号外完全相同,4个人按顺序依次从中摸出1个球,求样本点的个数.
解:4个人按顺序依次从袋中摸出1个球的所有可能结果用树状图表示如图所示:
共24个样本点.
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
素养点睛:本题考查了数学抽象和数学运算的核心素养.
题型2 古典概型的概率计算
2.从1,2,3,4,5这五个数字中任取三个不同的数字,求下列事件的概率:
(1)事件A={三个数字中不含1和5};
(2)事件B={三个数字中含1或5}.
解:这个试验的基本事件为:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),所以基本事件总数n=10.
题型3 较复杂的古典概型的概率计算
【答案】A
解:将A,B,C,D四位贵宾就座情况用下面图形表示出来:
如上图所示,本题中的等可能基本事件共有24个.
解决有序和无序问题应注意两点
(1)不放回抽样,既可看成是有序的,也可看成是无序的,不影响结果,但必须注意观察角度要一致.
(2)放回抽样,注意在连续抽取两次时因顺序不同所得到的样本点也不同,所以存在顺序.
(2020年攀枝花模拟)为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了n户家庭进行问卷调查.经调查发现,这些家庭的月收人在5 000元到8 000元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一、三、四小组的频率之比为1∶3∶6,且第四小组的频数为18.
规范解答——古典概型与统计的综合
(1)求n;
(2)求这n户家庭月收人的众数与中位数(结果精确到0.1);
(3)这n户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取6户家庭,并从这6户家庭中随机抽取2户家庭进行慰问,求这2户家庭月收入至多有一户超过6 000元的概率.
题后反思:概率问题常常与统计问题结合在一起考查,在此类问题中,概率与频率的区别并不是十分明显,通常直接用题目中的频率代替概率进行计算.解决与古典概型的交汇的问题,应明确相关事件,列举样本点,然后利用古典概型的概率计算公式求解.
| 素养达成 |
1.某校高一年级要组建数学、计算机、航空模型三个兴趣小组,某学生只选报其中的2个,则基本事件共有 ( )
A.1个 B.2个
C.3个 D.4个
【答案】C
【解析】该生选报的所有可能情况:{数学和计算机},{数学和航空模型},{计算机和航空模型},所以基本事件有3个.故选C.
2.下列试验中是古典概型的是 ( )
A.种下一粒花生,观察它是否发芽
B.向正方形ABCD内,任意投掷一点P,观察点P是否与正方形的中心O重合
C.从1,2,3,4四个数中,任取两个数,求所取两数之积是2的概率
D.在区间[0,5]内任取一点,求此点小于2的概率
【答案】C
【解析】A中花生发芽与不发芽的概率不一定相等,故不是古典概型,B,D中的试验中的基本事件有无数多个,不是古典概型;C中试验有6个基本事件,且每个基本事件发生的概率相同,是古典概型.故选C.
【答案】D
【答案】C
5.一个盒子内放有5个完全相同的小球,其上分别标有号码1,2,3,4,5.从中任取一个,记下号数后放回,再取出1个,记下号数后放回,按顺序记录为(x,y),试写出“所得两球的号数和为6”所包含的基本事件.
解:列表表示所有的基本事件.
由上表可直观地看出,“所得两球的号数和为
6”包含以下5个基本事件:(1,5),(2,4),(3,3),(4,
2),(5,1).
| 课后提能训练 |
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
