10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(47张PPT)
文档属性
| 名称 | 10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 17:56:23 | ||
图片预览









文档简介
第十章 概率
10.2 事件的相互独立性
学习目标
素养要求
1.结合有限样本空间,了解两个随机事件独立性的含义
数学抽象
2.结合古典概型,利用独立性计算概率
数学运算、数学建模
| 自学导引 |
相互独立事件的定义和性质
P(A)P(B)
【提示】
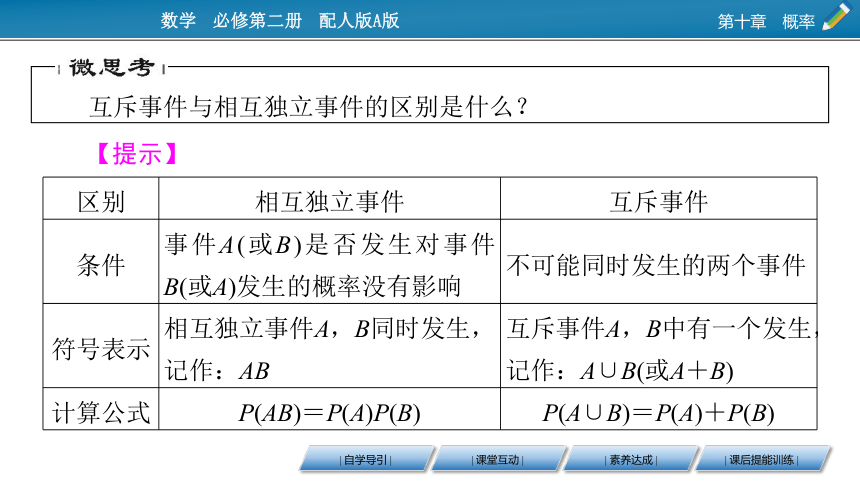
互斥事件与相互独立事件的区别是什么?
区别
相互独立事件
互斥事件
条件
事件A(或B)是否发生对事件B(或A)发生的概率没有影响
不可能同时发生的两个事件
符号表示
相互独立事件A,B同时发生,记作:AB
互斥事件A,B中有一个发生,记作:A∪B(或A+B)
计算公式
P(AB)=P(A)P(B)
P(A∪B)=P(A)+P(B)
1.若事件A,B相互独立,则P(AB)=P(A)P(B);
2.若事件A1,A2,…,An相互独立,则P(A1A2…An)=P(A1)·P(A2)·…·P(An).
独立事件的概率公式
【预习自测】
在某道路A,B,C三处设有交通灯,这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒,某辆车在这条道路上匀速行驶,则三处都不停车的概率为________.
| 课堂互动 |
一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
素养点睛:本题考查了数学抽象核心素养.
题型1 相互独立事件的判断
判断两个事件是否相互独立的两种方法
(1)根据问题的实质,从影响上看一事件的发生是否影响另一事件发生的概率来判断,若没有影响,则两个事件就是相互独立事件;
(2)定义法:通过式子P(AB)=P(A)P(B)来判断两个事件是否独立,若上式成立,则事件A,B相互独立,这是定量判断.
1.分别抛掷两枚质地均匀的硬币,设事件A是“第一枚为正面”,事件B是“第二枚为正面”,事件C是“两枚结果相同”,则A,B,C中具有相互独立性的有____________________________.
【答案】①A,B;②A,C;③B,C.
【解析】根据事件相互独立的定义判断,只要P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C)成立即可.利用古典概型概率公式计算可得P(A)=0.5,P(B)=0.5,P(C)=0.5,P(AB)=0.25,P(AC)=0.25,P(BC)=0.25.可以验证P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C).所以根据事件相互独立的定义,事件A与B相互独立,事件B与C相互独立,事件A与C相互独立.
王敏某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率;
(2)这三列火车至少有一列正点到达的概率.
题型2 相互独立事件同时发生的概率
【例题迁移1】 (变换问法)在本例条件下,求恰有一列火车正点到达的概率.
【例题迁移2】 (变换问法)若一列火车正点到达记10分,用ξ表示三列火车的总得分,求P(ξ≤20).
素养点睛:本题考查了数学运算与数学建模的核心素养.
解:事件“ξ≤20”表示“至多两列火车正点到达”,其对立事件为“三列火车都正点到达”,所以P(ξ≤20)=1-P(ABC)=1-P(A)P(B)P(C)=1-0.8×0.7×0.9=0.496.
题型3 相互独立事件的综合应用
(1)求甲、乙两人所付租车费用相同的概率;
(2)设ξ为甲、乙两人所付的租车费用之和,求P(ξ=4)和P(ξ=6)的值.
素养点睛:本题考查了数学建模和数学运算的核心素养.
概率问题中的数学思想
(1)正难则反.灵活应用对立事件间的概率关系(P(A)+P()=1)简化问题,是求解概率问题最常用的方法.
(2)化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.“所求事件”分几类(考虑加法公式转化为互斥事件)还是分几步组成(考虑乘法公式转化为相互独立事件).
(3)方程思想.利用有关的概率公式和问题中的数量关系,建立方程(组),通过解方程(组)使问题获解.
【答案】B
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知学生小张只选甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示小张选修的课程门数和没有选修的课程门数的乘积.
(1)求学生小张选修甲的概率;
(2)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率.
巧题妙解——相互独立事件概率公式的逆用
(2)若函数f(x)=x2+ξx为R上的偶函数,则ξ=0.当ξ=0时,表示小张选修三门功课或三门功课都没选.∴P(A)=P(ξ=0)=xyz+(1-x)(1-y)(1-z)=0.4×0.6×0.5+(1-0.4)(1-0.6)(1-0.5)=0.24,∴事件A的概率为0.24.
题后反思:对于相互独立事件的概率公式的逆用问题,仍按正向解决的原则进行解题,即可先设出一些未知量,再根据已知条件列出相应的方程组,由方程组求出未知量,从而解决问题.
| 素养达成 |
与相互独立事件A,B有关的概率计算公式(体现数学运算的核心素养).
【答案】A
【答案】C
3.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是________.
【答案】0.26
【解析】所求概率p=0.8×0.1+0.2×0.9=0.26.
5.某人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第3次拨号才接通电话;
(2)拨号不超过3次而接通电话.
| 课后提能训练 |
10.2 事件的相互独立性
学习目标
素养要求
1.结合有限样本空间,了解两个随机事件独立性的含义
数学抽象
2.结合古典概型,利用独立性计算概率
数学运算、数学建模
| 自学导引 |
相互独立事件的定义和性质
P(A)P(B)
【提示】
互斥事件与相互独立事件的区别是什么?
区别
相互独立事件
互斥事件
条件
事件A(或B)是否发生对事件B(或A)发生的概率没有影响
不可能同时发生的两个事件
符号表示
相互独立事件A,B同时发生,记作:AB
互斥事件A,B中有一个发生,记作:A∪B(或A+B)
计算公式
P(AB)=P(A)P(B)
P(A∪B)=P(A)+P(B)
1.若事件A,B相互独立,则P(AB)=P(A)P(B);
2.若事件A1,A2,…,An相互独立,则P(A1A2…An)=P(A1)·P(A2)·…·P(An).
独立事件的概率公式
【预习自测】
在某道路A,B,C三处设有交通灯,这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒,某辆车在这条道路上匀速行驶,则三处都不停车的概率为________.
| 课堂互动 |
一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
素养点睛:本题考查了数学抽象核心素养.
题型1 相互独立事件的判断
判断两个事件是否相互独立的两种方法
(1)根据问题的实质,从影响上看一事件的发生是否影响另一事件发生的概率来判断,若没有影响,则两个事件就是相互独立事件;
(2)定义法:通过式子P(AB)=P(A)P(B)来判断两个事件是否独立,若上式成立,则事件A,B相互独立,这是定量判断.
1.分别抛掷两枚质地均匀的硬币,设事件A是“第一枚为正面”,事件B是“第二枚为正面”,事件C是“两枚结果相同”,则A,B,C中具有相互独立性的有____________________________.
【答案】①A,B;②A,C;③B,C.
【解析】根据事件相互独立的定义判断,只要P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C)成立即可.利用古典概型概率公式计算可得P(A)=0.5,P(B)=0.5,P(C)=0.5,P(AB)=0.25,P(AC)=0.25,P(BC)=0.25.可以验证P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C).所以根据事件相互独立的定义,事件A与B相互独立,事件B与C相互独立,事件A与C相互独立.
王敏某天乘火车从重庆到上海去办事,若当天从重庆到上海的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率;
(2)这三列火车至少有一列正点到达的概率.
题型2 相互独立事件同时发生的概率
【例题迁移1】 (变换问法)在本例条件下,求恰有一列火车正点到达的概率.
【例题迁移2】 (变换问法)若一列火车正点到达记10分,用ξ表示三列火车的总得分,求P(ξ≤20).
素养点睛:本题考查了数学运算与数学建模的核心素养.
解:事件“ξ≤20”表示“至多两列火车正点到达”,其对立事件为“三列火车都正点到达”,所以P(ξ≤20)=1-P(ABC)=1-P(A)P(B)P(C)=1-0.8×0.7×0.9=0.496.
题型3 相互独立事件的综合应用
(1)求甲、乙两人所付租车费用相同的概率;
(2)设ξ为甲、乙两人所付的租车费用之和,求P(ξ=4)和P(ξ=6)的值.
素养点睛:本题考查了数学建模和数学运算的核心素养.
概率问题中的数学思想
(1)正难则反.灵活应用对立事件间的概率关系(P(A)+P()=1)简化问题,是求解概率问题最常用的方法.
(2)化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.“所求事件”分几类(考虑加法公式转化为互斥事件)还是分几步组成(考虑乘法公式转化为相互独立事件).
(3)方程思想.利用有关的概率公式和问题中的数量关系,建立方程(组),通过解方程(组)使问题获解.
【答案】B
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知学生小张只选甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示小张选修的课程门数和没有选修的课程门数的乘积.
(1)求学生小张选修甲的概率;
(2)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率.
巧题妙解——相互独立事件概率公式的逆用
(2)若函数f(x)=x2+ξx为R上的偶函数,则ξ=0.当ξ=0时,表示小张选修三门功课或三门功课都没选.∴P(A)=P(ξ=0)=xyz+(1-x)(1-y)(1-z)=0.4×0.6×0.5+(1-0.4)(1-0.6)(1-0.5)=0.24,∴事件A的概率为0.24.
题后反思:对于相互独立事件的概率公式的逆用问题,仍按正向解决的原则进行解题,即可先设出一些未知量,再根据已知条件列出相应的方程组,由方程组求出未知量,从而解决问题.
| 素养达成 |
与相互独立事件A,B有关的概率计算公式(体现数学运算的核心素养).
【答案】A
【答案】C
3.有甲、乙两批种子,发芽率分别为0.8和0.9,在两批种子中各取一粒,则恰有一粒种子能发芽的概率是________.
【答案】0.26
【解析】所求概率p=0.8×0.1+0.2×0.9=0.26.
5.某人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第3次拨号才接通电话;
(2)拨号不超过3次而接通电话.
| 课后提能训练 |
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
