2020--2021学年人教版九年级数学下册第二十七章相似单元练习题(word版含答案)
文档属性
| 名称 | 2020--2021学年人教版九年级数学下册第二十七章相似单元练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 650.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 07:48:43 | ||
图片预览



文档简介
人教版九年级数学下册第二十七章《相似》单元练习题(含答案)
一、单选题
1.已知点是线段的黄金分割点,若,则的长是( )
A. B. C. D.
2.如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( )
A.16 cm B.48 cm C. cm D.4 cm
3.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
4.如图,在△ABC 中,DE∥BC,DF∥AG,若,则下列结论正确的是( )
A. B. C. D.
5.如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=4,BC=6,CE=2,则CF的长等于( )
A.1 B.1.5 C.2 D.3
6.如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
7.如图,在正方形中,为边的中点,、分别为、边上的点,若,,,则的长为( )
A.2 B.3 C. D.
8.如图,点是的边上一点, ,如果的面积为15,那么的面积为( )
A.20 B.22.5 C.25 D.30
9.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C.4.8 D.7.2
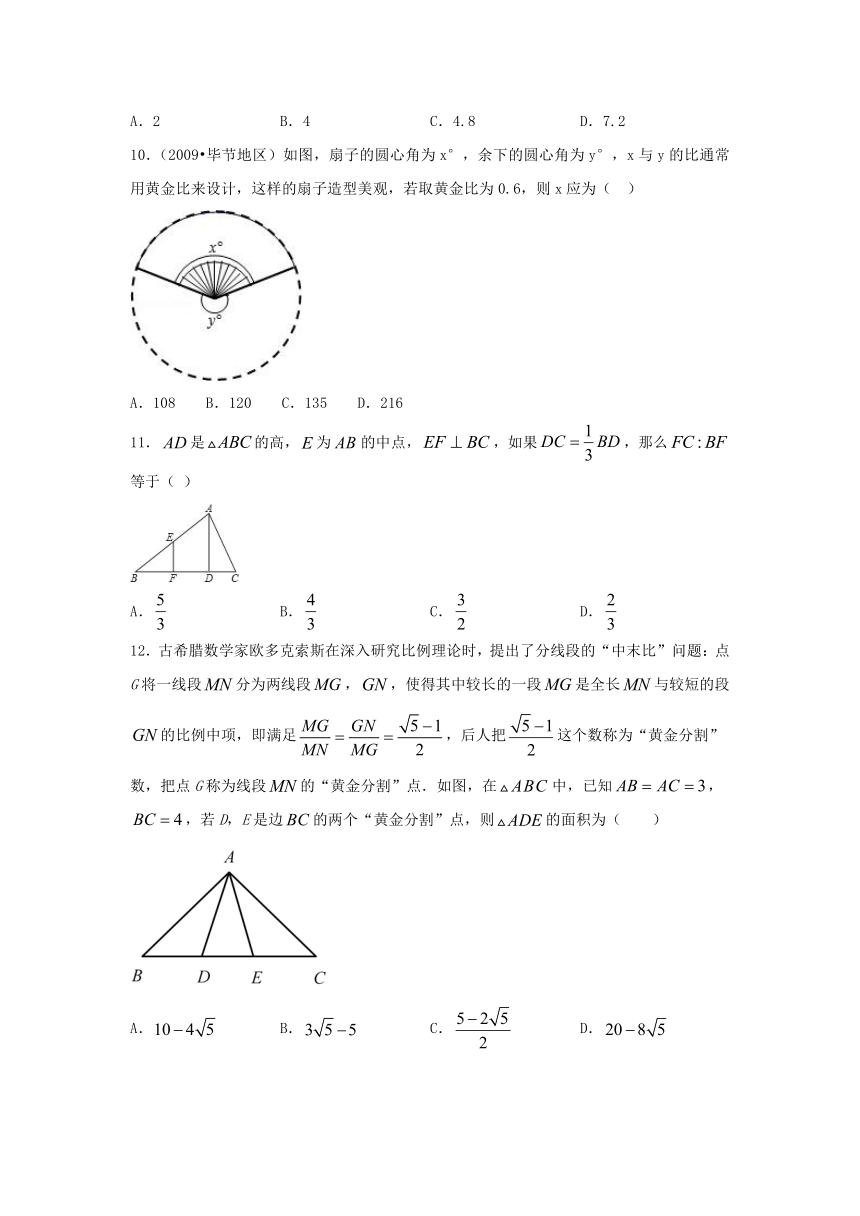
10.(2009?毕节地区)如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x应为( )
A.108 B.120 C.135 D.216
11.是的高,为的中点,,如果,那么等于( )
A. B. C. D.
12.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
二、填空题
13.如图,正方形的对角线上有一点,且,点在的延长线上,连接,过点作,交的延长线于点,连接并延长,交的延长线于点,若,,则线段的长是__________.
14.上小学五年级的小丽看见上初中的哥哥小勇用测树的影长和自己的影长的方法来测树高,她也学着哥哥的样子在同一时刻测得树的影长为5米,自己的影长为1米.要求得树高,还应测得____
15.两个相似多边形的周长之比为1∶3,则它们面积之比为______.
16.如图,已知矩形纸片ABCD,点E在边AB上,且,将沿直线CE翻折,使点B落在对角线AC上的点F处,联结DF,如果点D,F,E在同一直线上,则线段AE的长为____.
17.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图示).当n=8时,共向外做出了 18个小等边三角形; 当n=k时,共向外做出了 3(k-2)个小等边三角形,这些小等边三角形的面积和是 3(k-2)k2S(用含k的式子表示).
18.已知:中,点是边的中点,点在边上,,,若以,,为顶点的三角形与相似,的长是____.
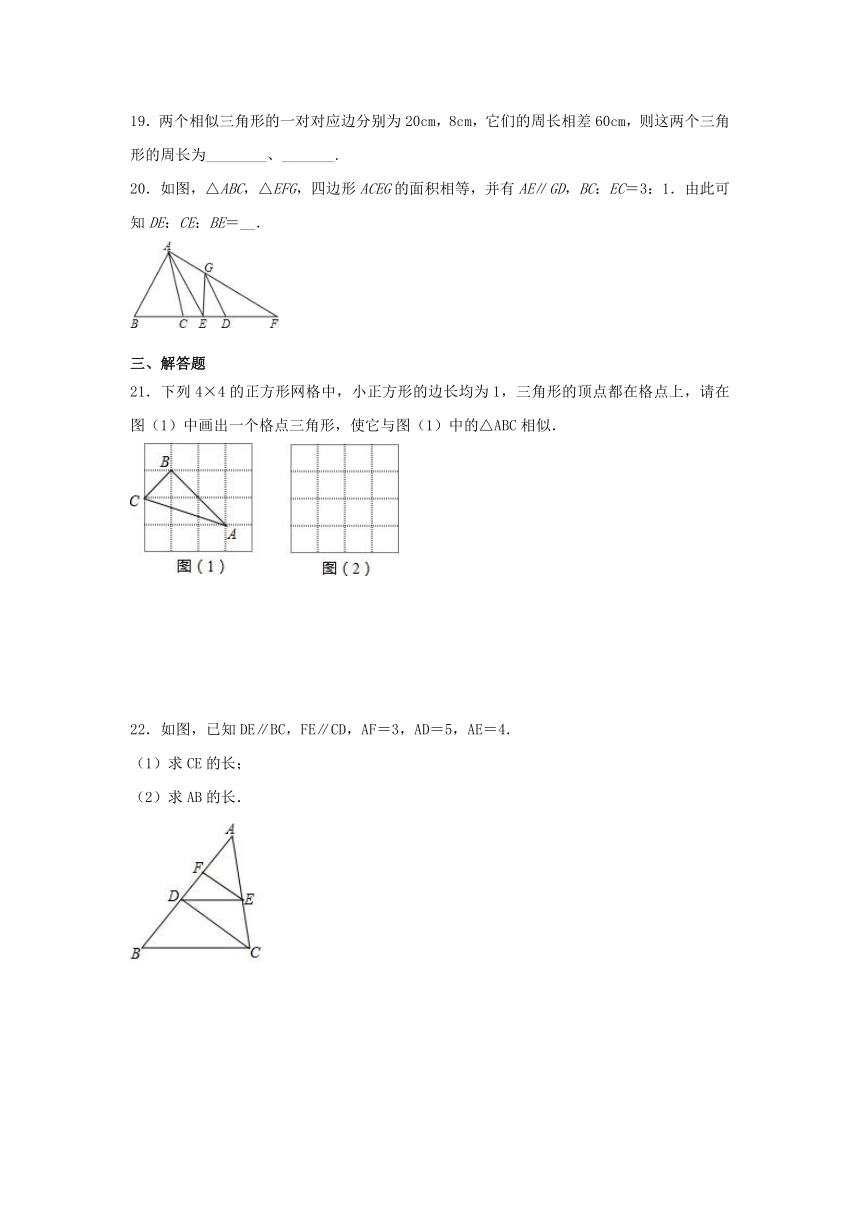
19.两个相似三角形的一对对应边分别为20cm,8cm,它们的周长相差60cm,则这两个三角形的周长为________、_______.
20.如图,△ABC,△EFG,四边形ACEG的面积相等,并有AE∥GD,BC:EC=3:1.由此可知DE:CE:BE=__.
三、解答题
21.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.
22.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
23.如图1,为半圆O的直径D为的延长线上一点,点C在半圆O上,且.
(1)求证:为圆切线;
(2)如图2,的平分线分别交、于点E、F,若,,求的长.
24.如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
25.如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
26.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AO=2,AT=,求AC的长.
27.如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
(1)求点D,O之间的距离;
(2)当tan∠CDO=时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
28.如图,Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
(1)用含t的代数式表示BD的长;
(2)求AB的长;
(3)求AB边上的高;
(4)当△BCD为等腰三角形时,求t的值
参考答案
1.A2.D3.B4.D5.B6.C7.B8.A9.C10.C11.A12.A
13.
14.她自己的身高
15.
16.
17.18 3(k-2)S
18.4或
19.100cm 40cm
20.2:1:4.
21.如图2,△A′B′C′为所作.
22.(1)CE=;(2)AB=.
23.证明:连接,
∵为的直径,∴,
∵,∴,
∵,∴,
∴,即,∴为的切线;
(2)在中,∵,,∴,
∵,,∴,
∴,
∵,,∴,
∴,
又
设,
∴,∴.∴.
24. 1)证明:∵AB=AC,CD=CA,∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,∴∠ECD=∠BAE,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,∴∠CED=∠AEB,∴△ABE≌△CDE(AAS);
(2)①当∠ABC的度数为60°时,四边形AOCE是菱形;
理由是:连接AO、OC.
∵四边形ABCE是圆内接四边形,∴∠ABC+∠AEC=180°.
∵∠ABC=60,∴∠AEC=120°=∠AOC.
∵OA=OC,∴∠OAC=∠OCA=30°.
∵AB=AC,∴△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=∠CAD+∠D.
∵AC=CD,∴∠CAD=∠D=30°,∴∠ACE=180°﹣120°﹣30°=30°,∴∠OAE=∠OCE=60°,∴四边形AOCE是平行四边形.
∵OA=OC,∴?AOCE是菱形;
②由(1)得:△ABE≌△CDE,∴BE=DE=8,AE=CE=6,∴∠D=∠EBC.
∵∠CED=∠ABC=∠ACB,∴△ECD∽△CFB,∴=.
∵∠AFE=∠BFC,∠AEB=∠FCB,∴△AEF∽△BCF,∴=,∴EF==.
故答案为①60°;②.
25.(1)∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,
理由如下:∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=BC,
又AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC,
∴△AFG∽△CBG,
∴
∴
∴AG=,
∵BD=5,AD是BC边上的中线,
∴BC=2BD=10,
∵∠BAC=90°,AB=8,
∴AC=,
∴AG==2,
故答案为2.
26.(1)AT平分∠BAC;(2)AC=3.
27.(1)2;(2);(3)
28.(1)BD=2t;(2)50cm;(3)24cm;(4)当△BCD是等腰三角形时,t的值为12.5秒或15秒或18秒
一、单选题
1.已知点是线段的黄金分割点,若,则的长是( )
A. B. C. D.
2.如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( )
A.16 cm B.48 cm C. cm D.4 cm
3.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
4.如图,在△ABC 中,DE∥BC,DF∥AG,若,则下列结论正确的是( )
A. B. C. D.
5.如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=4,BC=6,CE=2,则CF的长等于( )
A.1 B.1.5 C.2 D.3
6.如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
A. B. C. D.
7.如图,在正方形中,为边的中点,、分别为、边上的点,若,,,则的长为( )
A.2 B.3 C. D.
8.如图,点是的边上一点, ,如果的面积为15,那么的面积为( )
A.20 B.22.5 C.25 D.30
9.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C.4.8 D.7.2
10.(2009?毕节地区)如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x应为( )
A.108 B.120 C.135 D.216
11.是的高,为的中点,,如果,那么等于( )
A. B. C. D.
12.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段分为两线段,,使得其中较长的一段是全长与较短的段的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段的“黄金分割”点.如图,在中,已知,,若D,E是边的两个“黄金分割”点,则的面积为( )
A. B. C. D.
二、填空题
13.如图,正方形的对角线上有一点,且,点在的延长线上,连接,过点作,交的延长线于点,连接并延长,交的延长线于点,若,,则线段的长是__________.
14.上小学五年级的小丽看见上初中的哥哥小勇用测树的影长和自己的影长的方法来测树高,她也学着哥哥的样子在同一时刻测得树的影长为5米,自己的影长为1米.要求得树高,还应测得____
15.两个相似多边形的周长之比为1∶3,则它们面积之比为______.
16.如图,已知矩形纸片ABCD,点E在边AB上,且,将沿直线CE翻折,使点B落在对角线AC上的点F处,联结DF,如果点D,F,E在同一直线上,则线段AE的长为____.
17.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图示).当n=8时,共向外做出了 18个小等边三角形; 当n=k时,共向外做出了 3(k-2)个小等边三角形,这些小等边三角形的面积和是 3(k-2)k2S(用含k的式子表示).
18.已知:中,点是边的中点,点在边上,,,若以,,为顶点的三角形与相似,的长是____.
19.两个相似三角形的一对对应边分别为20cm,8cm,它们的周长相差60cm,则这两个三角形的周长为________、_______.
20.如图,△ABC,△EFG,四边形ACEG的面积相等,并有AE∥GD,BC:EC=3:1.由此可知DE:CE:BE=__.
三、解答题
21.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.
22.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
23.如图1,为半圆O的直径D为的延长线上一点,点C在半圆O上,且.
(1)求证:为圆切线;
(2)如图2,的平分线分别交、于点E、F,若,,求的长.
24.如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
25.如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
26.如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
(1)求证:AT平分∠BAC;
(2)若AO=2,AT=,求AC的长.
27.如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
(1)求点D,O之间的距离;
(2)当tan∠CDO=时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
28.如图,Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
(1)用含t的代数式表示BD的长;
(2)求AB的长;
(3)求AB边上的高;
(4)当△BCD为等腰三角形时,求t的值
参考答案
1.A2.D3.B4.D5.B6.C7.B8.A9.C10.C11.A12.A
13.
14.她自己的身高
15.
16.
17.18 3(k-2)S
18.4或
19.100cm 40cm
20.2:1:4.
21.如图2,△A′B′C′为所作.
22.(1)CE=;(2)AB=.
23.证明:连接,
∵为的直径,∴,
∵,∴,
∵,∴,
∴,即,∴为的切线;
(2)在中,∵,,∴,
∵,,∴,
∴,
∵,,∴,
∴,
又
设,
∴,∴.∴.
24. 1)证明:∵AB=AC,CD=CA,∴∠ABC=∠ACB,AB=CD.
∵四边形ABCE是圆内接四边形,∴∠ECD=∠BAE,∠CED=∠ABC.
∵∠ABC=∠ACB=∠AEB,∴∠CED=∠AEB,∴△ABE≌△CDE(AAS);
(2)①当∠ABC的度数为60°时,四边形AOCE是菱形;
理由是:连接AO、OC.
∵四边形ABCE是圆内接四边形,∴∠ABC+∠AEC=180°.
∵∠ABC=60,∴∠AEC=120°=∠AOC.
∵OA=OC,∴∠OAC=∠OCA=30°.
∵AB=AC,∴△ABC是等边三角形,∴∠ACB=60°.
∵∠ACB=∠CAD+∠D.
∵AC=CD,∴∠CAD=∠D=30°,∴∠ACE=180°﹣120°﹣30°=30°,∴∠OAE=∠OCE=60°,∴四边形AOCE是平行四边形.
∵OA=OC,∴?AOCE是菱形;
②由(1)得:△ABE≌△CDE,∴BE=DE=8,AE=CE=6,∴∠D=∠EBC.
∵∠CED=∠ABC=∠ACB,∴△ECD∽△CFB,∴=.
∵∠AFE=∠BFC,∠AEB=∠FCB,∴△AEF∽△BCF,∴=,∴EF==.
故答案为①60°;②.
25.(1)∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,
理由如下:∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=BC,
又AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC,
∴△AFG∽△CBG,
∴
∴
∴AG=,
∵BD=5,AD是BC边上的中线,
∴BC=2BD=10,
∵∠BAC=90°,AB=8,
∴AC=,
∴AG==2,
故答案为2.
26.(1)AT平分∠BAC;(2)AC=3.
27.(1)2;(2);(3)
28.(1)BD=2t;(2)50cm;(3)24cm;(4)当△BCD是等腰三角形时,t的值为12.5秒或15秒或18秒
