第6章 实数 章末复习 课件(共22张PPT)
文档属性
| 名称 | 第6章 实数 章末复习 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 10:54:46 | ||
图片预览







文档简介
(共22张PPT)
章末复习
第6章
实
数
沪科版·七年级数学下册
上课课件
学习目标
【知识与技能】
进一步加深对平方根、立方根、无理数、实数概念的理解,会求平方根、立方根,会比较实数的大小,能运用实数的运算解决具体问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想,转化思想,类比思想,加深对本章知识的理解和应用.
【情感态度】
在运用实数的有关知识解决具体问题的过程中,进一步体会数学与生活的密切联系,增强学生的数学应用意识,激发学生学习兴趣.
【教学重点】
实数的运算及大小比较.
【教学难点】
运用实数的有关知识解决具体问题.
内容整理
开方运算
平方根
立方根
实数
平方根
立方根
知识回顾
1.
如果一个数的平方等于a,那么这个数叫做a的平方根,其中正的平方根也叫做a的算术平方根.求一个数的平方根的运算叫做开平方.
一、平方根、算术平方根、立方根
2.
如果一个数的立方等于a,那么这个数叫做a的立方根.求一个数的立方根的运算叫做开立方.
二、无理数、实数
无限不循环小数叫做无理数,无理数和有理数统称为实数,实数与数轴上的点一一对应.
三、实数的性质
在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样,实数a的相反数是-a,倒数是
(a≠0),绝对值是|a|.
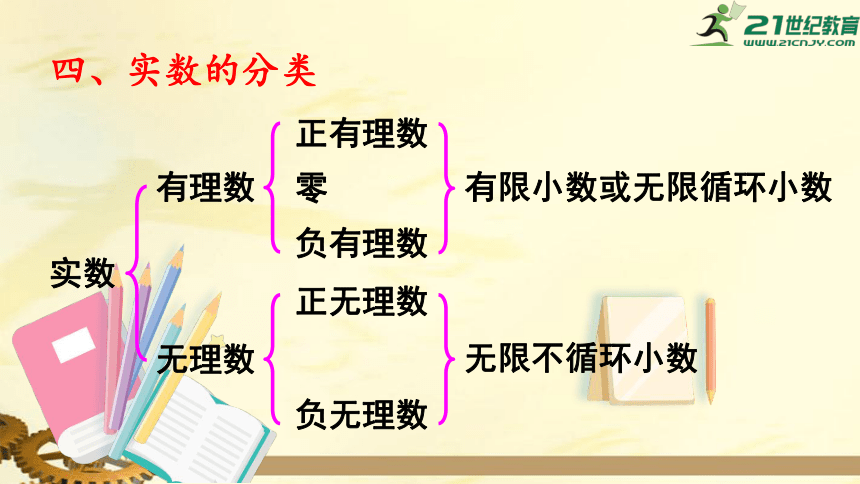
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
四、实数的分类
五、实数的运算及大小比较
实数的加、减、乘、除、乘方、非负数开平方、实数开立方运算具有与有理数相同的运算法则和运算律.
在实数范围内也有:正数大于零、负数小于零、正数大于负数;两个正数、绝对值大的数较大;两个负数,绝对值大的数反而小.
典例精析
例1
把下面各数填在相应的括号里:
有理数集合:{
};
无理数集合:{
}.
【分析】对实数进行分类,应先对某些数进行计算或化简,然后根据它的最后结果进行回答,不能只看表面形式.
例2
已知
,则
a
+
b
=(
):
A.﹣8
B.﹣6
C.6
D.8
【分析】由绝对值和算术平方根的非负性可得:
,∴
,∴a+b=-6,故选B.
B
例3
计算:
【分析】按实数的运算法则,运算性质和运算顺序进行计算.
解:(1)原式=
(2)原式=
例4
已知a、b互为倒数,c、d互为相反数,m为2的算术平方根,求
.
【分析】由a、b互为倒数可得ab=1,则c、d互为相反数可得c+d=0,由m为2的算术平方根可得m=
.
解
由题意得:ab=1,c+d=0,m=
.
∴原式=
.
随堂练习
1.已知实数x、y满足
,则x-y等于
(
)
A.3
B.-3
C.1
D.-1
A
2.
把下列各数填入相应的集合里:
有理数集合:{
}
无理数集合:{
}
正实数集合:{
}
负实数集合:{
}
3.已知
≈1.732,
≈5.477,求值:
(1)
≈_______
(2)
≈
_______
(3)
≈_______
(4)
≈
_______
4.比较大小.
(1)
与
0.1
;
(2)
与
.
17.32
0.5477
0.1732
54.77
5.已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+10b的平方根.
解:由题意得
解得
∴a+10b=25.
∴a+10b的平方根为±5.
6.已知
的整数部分为a,2+
的小数部分为b,求
a
+
b
的值.
解:∵
∴a=3,b=2+
-4=
-2.
∴a+b=3+
-2=
+1.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第3题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
章末复习
第6章
实
数
沪科版·七年级数学下册
上课课件
学习目标
【知识与技能】
进一步加深对平方根、立方根、无理数、实数概念的理解,会求平方根、立方根,会比较实数的大小,能运用实数的运算解决具体问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想,转化思想,类比思想,加深对本章知识的理解和应用.
【情感态度】
在运用实数的有关知识解决具体问题的过程中,进一步体会数学与生活的密切联系,增强学生的数学应用意识,激发学生学习兴趣.
【教学重点】
实数的运算及大小比较.
【教学难点】
运用实数的有关知识解决具体问题.
内容整理
开方运算
平方根
立方根
实数
平方根
立方根
知识回顾
1.
如果一个数的平方等于a,那么这个数叫做a的平方根,其中正的平方根也叫做a的算术平方根.求一个数的平方根的运算叫做开平方.
一、平方根、算术平方根、立方根
2.
如果一个数的立方等于a,那么这个数叫做a的立方根.求一个数的立方根的运算叫做开立方.
二、无理数、实数
无限不循环小数叫做无理数,无理数和有理数统称为实数,实数与数轴上的点一一对应.
三、实数的性质
在实数范围内,相反数、倒数、绝对值的意义与在有理数范围内完全一样,实数a的相反数是-a,倒数是
(a≠0),绝对值是|a|.
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
四、实数的分类
五、实数的运算及大小比较
实数的加、减、乘、除、乘方、非负数开平方、实数开立方运算具有与有理数相同的运算法则和运算律.
在实数范围内也有:正数大于零、负数小于零、正数大于负数;两个正数、绝对值大的数较大;两个负数,绝对值大的数反而小.
典例精析
例1
把下面各数填在相应的括号里:
有理数集合:{
};
无理数集合:{
}.
【分析】对实数进行分类,应先对某些数进行计算或化简,然后根据它的最后结果进行回答,不能只看表面形式.
例2
已知
,则
a
+
b
=(
):
A.﹣8
B.﹣6
C.6
D.8
【分析】由绝对值和算术平方根的非负性可得:
,∴
,∴a+b=-6,故选B.
B
例3
计算:
【分析】按实数的运算法则,运算性质和运算顺序进行计算.
解:(1)原式=
(2)原式=
例4
已知a、b互为倒数,c、d互为相反数,m为2的算术平方根,求
.
【分析】由a、b互为倒数可得ab=1,则c、d互为相反数可得c+d=0,由m为2的算术平方根可得m=
.
解
由题意得:ab=1,c+d=0,m=
.
∴原式=
.
随堂练习
1.已知实数x、y满足
,则x-y等于
(
)
A.3
B.-3
C.1
D.-1
A
2.
把下列各数填入相应的集合里:
有理数集合:{
}
无理数集合:{
}
正实数集合:{
}
负实数集合:{
}
3.已知
≈1.732,
≈5.477,求值:
(1)
≈_______
(2)
≈
_______
(3)
≈_______
(4)
≈
_______
4.比较大小.
(1)
与
0.1
;
(2)
与
.
17.32
0.5477
0.1732
54.77
5.已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+10b的平方根.
解:由题意得
解得
∴a+10b=25.
∴a+10b的平方根为±5.
6.已知
的整数部分为a,2+
的小数部分为b,求
a
+
b
的值.
解:∵
∴a=3,b=2+
-4=
-2.
∴a+b=3+
-2=
+1.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第3题;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
