6.2.1 理数与实数的概念 课件(共24张PPT)
文档属性
| 名称 | 6.2.1 理数与实数的概念 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览


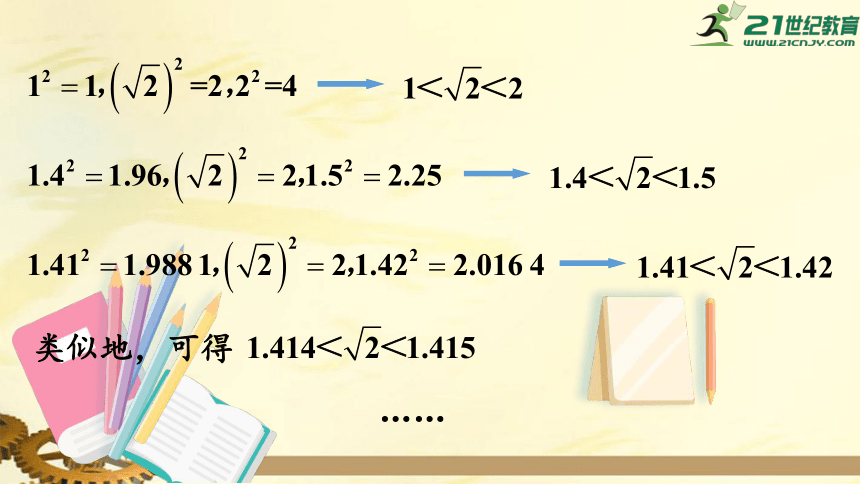



文档简介
(共24张PPT)
6.2
实数
第1课时
无理数与实数的概念
沪科版·七年级数学下册
上课课件
第6章
实
数
学习目标
【知识与技能】
1.了解无理数和实数的概念.
2.会对实数进行分类.
3.会用“夹逼法”估计一个无理数的大小,会将循环小数化为分数.
【过程与方法】
从实际问题引出无理数,会用“夹逼法”估计无理数的大小,能用两种方法对实数进行分类,增强学生的参与意识,发挥学生的积极主动性.
【情感态度】
让学生在独立思考的基础上,积极参与数学问题的讨论,勇于发表自己的观点,增强合作交流意识,激发学生的学习兴趣.
【教学重点】
掌握无理数的三种形式,能够识别有理数和无理数,能对实数进行分类.
【教学难点】
循环小数化为分数的规律与方法.
新课导入
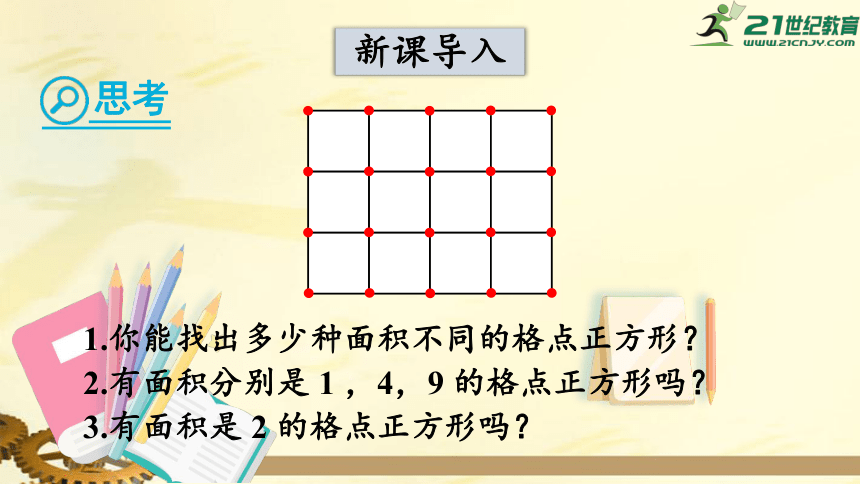
思考
1.你能找出多少种面积不同的格点正方形?
2.有面积分别是
1
,4,9
的格点正方形吗?
3.有面积是
2
的格点正方形吗?
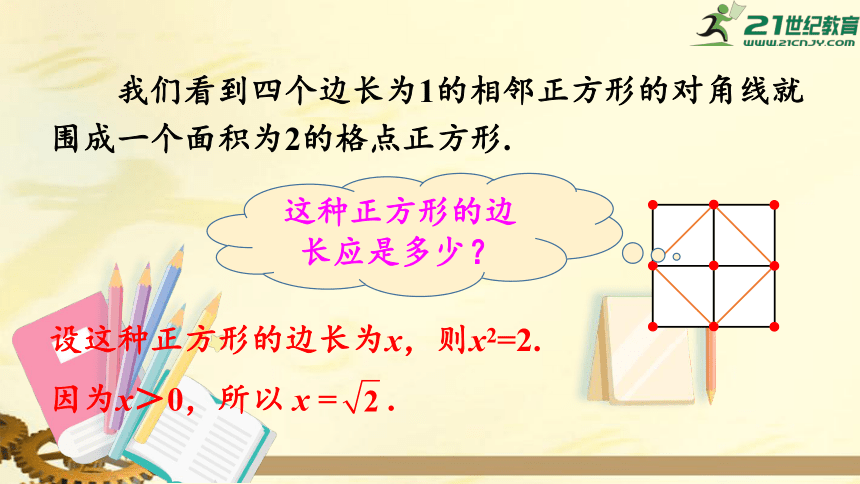
我们看到四个边长为1的相邻正方形的对角线就围成一个面积为2的格点正方形.
这种正方形的边长应是多少?
设这种正方形的边长为x,则x2=2.
因为x>0,所以
x
=
.
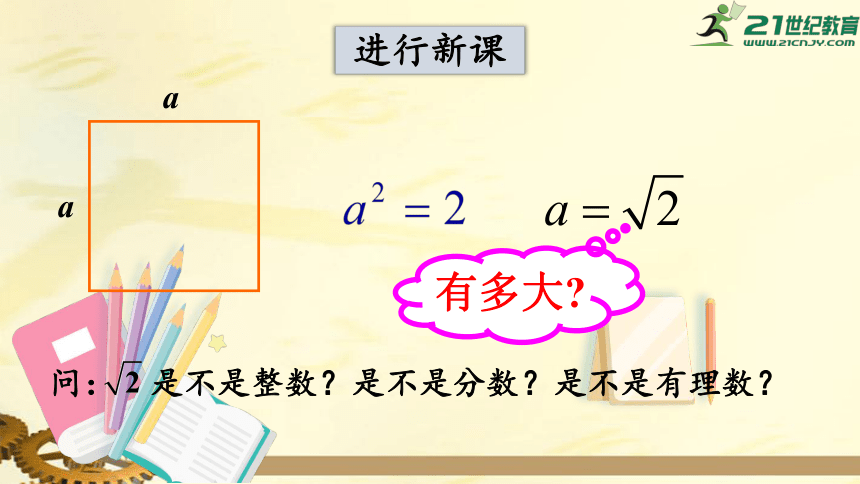
进行新课
问:
是不是整数?是不是分数?是不是有理数?
有多大?
a
a
类似地,可得
……
像上面这样一直(无限)做下去,我们可以得到:
这说明
是一个无限不循环小数.
我们把这种无限不循环小数叫做无理数.
思考:你知道哪些数是无理数?
1.圆周率π及一些含有π的数都是无理数.
例如:
2.开不尽方的数都是无理数.
像
都是无理数.
注意:带根号的数不一定是无理数.
例如:
因为
,所以
是有理数.
3.有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
168.3232232223…〔两个3之间依次多1个2〕
0.12345678910111213
…〔小数部分由相继的正整数组成〕
无理数也像有理数一样广泛存在着.
无理数也有正负之分,例如:
正无理数:
负无理数:
知识回顾
有理数
整数
分数
正整数
零
负整数
正分数
负分数
知识回顾
思考:有理数还有分类方法吗?
有理数
正有理数
零
负有理数
知识回顾
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数(均可化为分数)
无理数(不可化为分数)
概念整理
有理数和无理数统称实数.
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
在
中,
练
习
属于有理数的:________________________________
属于无理数的:________________________________
属于实数的有:________________________________
随堂练习
1.
有理数和无理数的区别在于(
)
A.有理数都是有限小数,无理数都是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正的,无理数是负的
D.有理数是正数,无理数是分数
B
2.
把下列各数填入相应的括号内:
(1)有理数:{
};
(2)无理数:{
};
(3)正实数:{
};
(4)实数:{
}.
3.
试将下列各数进行分类(用两种不同的标准分类):
4.
写出满足条件:①是负数;②是无限不循环小数的一个数是________.
5.
在
0,1,2,3,4,5,6,7,8,9,10
这11个数中,
(1)______的平方根和______的立方根是有理数;
(2)____________的平方根和______________的立方根是无理数.
﹣π
答案不唯一
0,1,4,9
0,1,8
2,3,5,6,7,8,10
2,3,4,5,6,7,9,10
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P12练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
6.2
实数
第1课时
无理数与实数的概念
沪科版·七年级数学下册
上课课件
第6章
实
数
学习目标
【知识与技能】
1.了解无理数和实数的概念.
2.会对实数进行分类.
3.会用“夹逼法”估计一个无理数的大小,会将循环小数化为分数.
【过程与方法】
从实际问题引出无理数,会用“夹逼法”估计无理数的大小,能用两种方法对实数进行分类,增强学生的参与意识,发挥学生的积极主动性.
【情感态度】
让学生在独立思考的基础上,积极参与数学问题的讨论,勇于发表自己的观点,增强合作交流意识,激发学生的学习兴趣.
【教学重点】
掌握无理数的三种形式,能够识别有理数和无理数,能对实数进行分类.
【教学难点】
循环小数化为分数的规律与方法.
新课导入
思考
1.你能找出多少种面积不同的格点正方形?
2.有面积分别是
1
,4,9
的格点正方形吗?
3.有面积是
2
的格点正方形吗?
我们看到四个边长为1的相邻正方形的对角线就围成一个面积为2的格点正方形.
这种正方形的边长应是多少?
设这种正方形的边长为x,则x2=2.
因为x>0,所以
x
=
.
进行新课
问:
是不是整数?是不是分数?是不是有理数?
有多大?
a
a
类似地,可得
……
像上面这样一直(无限)做下去,我们可以得到:
这说明
是一个无限不循环小数.
我们把这种无限不循环小数叫做无理数.
思考:你知道哪些数是无理数?
1.圆周率π及一些含有π的数都是无理数.
例如:
2.开不尽方的数都是无理数.
像
都是无理数.
注意:带根号的数不一定是无理数.
例如:
因为
,所以
是有理数.
3.有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
168.3232232223…〔两个3之间依次多1个2〕
0.12345678910111213
…〔小数部分由相继的正整数组成〕
无理数也像有理数一样广泛存在着.
无理数也有正负之分,例如:
正无理数:
负无理数:
知识回顾
有理数
整数
分数
正整数
零
负整数
正分数
负分数
知识回顾
思考:有理数还有分类方法吗?
有理数
正有理数
零
负有理数
知识回顾
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数(均可化为分数)
无理数(不可化为分数)
概念整理
有理数和无理数统称实数.
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
在
中,
练
习
属于有理数的:________________________________
属于无理数的:________________________________
属于实数的有:________________________________
随堂练习
1.
有理数和无理数的区别在于(
)
A.有理数都是有限小数,无理数都是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正的,无理数是负的
D.有理数是正数,无理数是分数
B
2.
把下列各数填入相应的括号内:
(1)有理数:{
};
(2)无理数:{
};
(3)正实数:{
};
(4)实数:{
}.
3.
试将下列各数进行分类(用两种不同的标准分类):
4.
写出满足条件:①是负数;②是无限不循环小数的一个数是________.
5.
在
0,1,2,3,4,5,6,7,8,9,10
这11个数中,
(1)______的平方根和______的立方根是有理数;
(2)____________的平方根和______________的立方根是无理数.
﹣π
答案不唯一
0,1,4,9
0,1,8
2,3,5,6,7,8,10
2,3,4,5,6,7,9,10
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P12练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
