6.1.3 立方根 课件(共24张PPT)
文档属性
| 名称 | 6.1.3 立方根 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 11:00:48 | ||
图片预览








文档简介
(共24张PPT)
2.立方根
沪科版·七年级数学下册
上课课件
第6章
实
数
6.1
平方根、立方根
学习目标
【知识与技能】
1.理解立方根的概念,会用符号表示一个数的立方根.
2.知道开立方与立方互为逆运算,会求某些数的立方根,理解并掌握立方根的性质.
3.能利用计算器求立方根.
【过程与方法】
通过观察、理解开立方运算和立方运算的互逆关系,掌握求一个数的立方根的方法,培养学生的演绎、归纳能力.
【情感态度】
在数学活动中激发学生自己探索的兴趣,通过合作交流,让学生体验成功的喜悦.
【教学重点】
会求一个数的立方根,掌握立方根的性质.
【教学难点】
理解开立方与立方的互逆关系.
复习导入
口答:
(1)什么是平方根?如何用符号表示a(a≥0)的平方根?
(2)正数有几个平方根?它们之间的关系是什么?
负数有没有平方根?0的平方根是什么?
进行新课
问题2
要做一个容积是64m3的正方体木箱,如图所示,问它的棱长是多少?
要求一个数,使它的立方等于64.
设正方体的棱长为
x
cm,则
这就是要求一个数,使它的立方等于64.
因为
所以
x=4.
正方体的棱长为
4
cm.
思考:(1)什么数的立方等于-8?
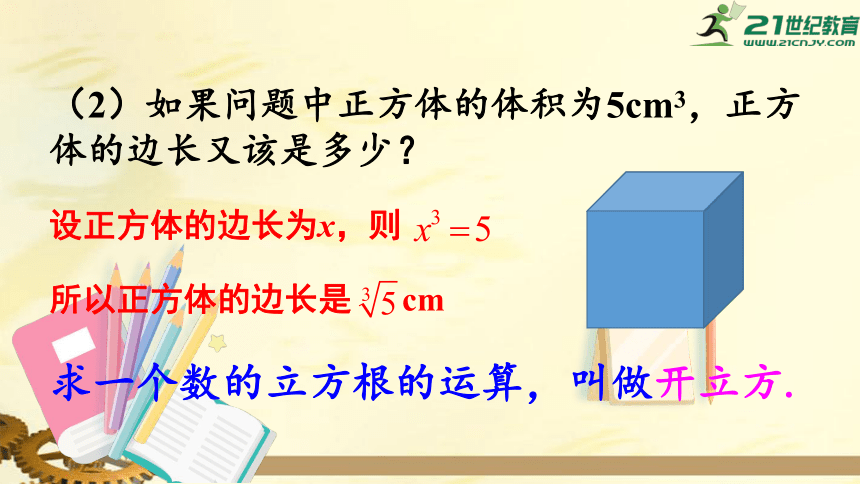
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
-2
一般地,一个数的立方等于a,这个数就叫做
a
的立方根,也叫做
a
的三次方根.
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号
a,
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的边长为x,则
所以正方体的边长是
cm
求一个数的立方根的运算,叫做开立方.
填一填:
1.
因为23=8,所以8的立方根是( )
2.
因为( )3
=
0.125,所以0.125的立方根是( )
3.
因为( )3
=
0,所以0的立方根是( )
4.
因为( )3
=-8,所以-8的立方根是(
)
5.
因为( )3
=-
,所以-
的立方根是(
)
你能看出正数,0,负数的立方根各有什么特点?
2
0
0
-2
-2
正数有立方根吗?如果有,有几个?负数呢?零呢?
想一想:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
你能归纳出平方根和立方根的异同点吗?
被开方数
平方根
立方根
正数
负数
零
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
例5
求下列各数的立方根:
(1)27;(2)﹣64;(3)0.
解(1)因为33=27,所以27的立方是3,即
.
(2)因为(﹣4)3=﹣64,所以﹣64的立方是﹣4,即
.
(3)因为03=0,所以0的立方是0,即
.
探究:
-7
-7
=
-8
-8
=
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
例6
用计算器求下列各数的立方根(精确到0.01):
(1)2;(2)7.797;(3)﹣17.456;(4)
.
解(1)在计算器上依次按键:
,显示结果是1.259
921
05,精确到0.01,得
.
2ndf
2
=
(2)
.
请同学们自己算出第(3)(4)题的结果.
随堂练习
1.
填空
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.
±1
1
1
0
±1
,
0
1
,
0
(5)
的立方根为________.
(6)
的平方根为________.
(7)
的立方根为________.
-2
-2
±2
2.若一个数的平方根为±8,则这个数的立方根是__________.
3.
如果一个数的立方根等于这个数的算术平方根,
那么这个数是(
)
A.0
B.0或1
C.1
D.±1或0
4.
下列各式正确的是(
)
A.
B.
C.
D.
4
B
B
5.
若a2=(-5)2,b3=(-5)3,则a
+
b的值为______.
6.
若x2-9=0,y3+27=0,则点P(y,-x)在第_______
象限.
7.(1)125的立方根是_______;
(2)
的立方根是_______.
0或-10
二或三
5
8.
判断下列说法是否正确,并说明理由.
(1)
的立方根是
(2)25的平方根是5
(3)﹣64没有立方根
(4)﹣4的平方根是±2
(5)0的平方根和立方根都是0
×
×
×
×
√
9.
求出下列各式中的未知数
x
.
(1)x3=729
(2)(x-1)3=125
(3)
(4)
10.
用计算器计算
x=9
x=6
x=8
x=66
解(1)在计算器上依次按键:
,显示结果是12.264
940
82,所以
.
2ndf
1845
=
课堂小结
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作
.
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
课后作业
1.完成课本P7练习1-4;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
2.立方根
沪科版·七年级数学下册
上课课件
第6章
实
数
6.1
平方根、立方根
学习目标
【知识与技能】
1.理解立方根的概念,会用符号表示一个数的立方根.
2.知道开立方与立方互为逆运算,会求某些数的立方根,理解并掌握立方根的性质.
3.能利用计算器求立方根.
【过程与方法】
通过观察、理解开立方运算和立方运算的互逆关系,掌握求一个数的立方根的方法,培养学生的演绎、归纳能力.
【情感态度】
在数学活动中激发学生自己探索的兴趣,通过合作交流,让学生体验成功的喜悦.
【教学重点】
会求一个数的立方根,掌握立方根的性质.
【教学难点】
理解开立方与立方的互逆关系.
复习导入
口答:
(1)什么是平方根?如何用符号表示a(a≥0)的平方根?
(2)正数有几个平方根?它们之间的关系是什么?
负数有没有平方根?0的平方根是什么?
进行新课
问题2
要做一个容积是64m3的正方体木箱,如图所示,问它的棱长是多少?
要求一个数,使它的立方等于64.
设正方体的棱长为
x
cm,则
这就是要求一个数,使它的立方等于64.
因为
所以
x=4.
正方体的棱长为
4
cm.
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
-2
一般地,一个数的立方等于a,这个数就叫做
a
的立方根,也叫做
a
的三次方根.
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号
a,
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的边长为x,则
所以正方体的边长是
cm
求一个数的立方根的运算,叫做开立方.
填一填:
1.
因为23=8,所以8的立方根是( )
2.
因为( )3
=
0.125,所以0.125的立方根是( )
3.
因为( )3
=
0,所以0的立方根是( )
4.
因为( )3
=-8,所以-8的立方根是(
)
5.
因为( )3
=-
,所以-
的立方根是(
)
你能看出正数,0,负数的立方根各有什么特点?
2
0
0
-2
-2
正数有立方根吗?如果有,有几个?负数呢?零呢?
想一想:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
你能归纳出平方根和立方根的异同点吗?
被开方数
平方根
立方根
正数
负数
零
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
例5
求下列各数的立方根:
(1)27;(2)﹣64;(3)0.
解(1)因为33=27,所以27的立方是3,即
.
(2)因为(﹣4)3=﹣64,所以﹣64的立方是﹣4,即
.
(3)因为03=0,所以0的立方是0,即
.
探究:
-7
-7
=
-8
-8
=
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
例6
用计算器求下列各数的立方根(精确到0.01):
(1)2;(2)7.797;(3)﹣17.456;(4)
.
解(1)在计算器上依次按键:
,显示结果是1.259
921
05,精确到0.01,得
.
2ndf
2
=
(2)
.
请同学们自己算出第(3)(4)题的结果.
随堂练习
1.
填空
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.
±1
1
1
0
±1
,
0
1
,
0
(5)
的立方根为________.
(6)
的平方根为________.
(7)
的立方根为________.
-2
-2
±2
2.若一个数的平方根为±8,则这个数的立方根是__________.
3.
如果一个数的立方根等于这个数的算术平方根,
那么这个数是(
)
A.0
B.0或1
C.1
D.±1或0
4.
下列各式正确的是(
)
A.
B.
C.
D.
4
B
B
5.
若a2=(-5)2,b3=(-5)3,则a
+
b的值为______.
6.
若x2-9=0,y3+27=0,则点P(y,-x)在第_______
象限.
7.(1)125的立方根是_______;
(2)
的立方根是_______.
0或-10
二或三
5
8.
判断下列说法是否正确,并说明理由.
(1)
的立方根是
(2)25的平方根是5
(3)﹣64没有立方根
(4)﹣4的平方根是±2
(5)0的平方根和立方根都是0
×
×
×
×
√
9.
求出下列各式中的未知数
x
.
(1)x3=729
(2)(x-1)3=125
(3)
(4)
10.
用计算器计算
x=9
x=6
x=8
x=66
解(1)在计算器上依次按键:
,显示结果是12.264
940
82,所以
.
2ndf
1845
=
课堂小结
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作
.
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
课后作业
1.完成课本P7练习1-4;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
