6.1.1平方根 课件(共22张PPT)
图片预览








文档简介
(共22张PPT)
第6章
实
数
6.1
平方根、立方根
1.平方根
第1课时
平方根
沪科版·七年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握平方根、算术平方根的概念,明确平方根和算术平方根之间的联系和区别;
2.能用符号表示一个数的平方根和算术平方根,理解开平方运算和平方运算之间的互逆关系.会求一个非负数的平方根和算术平方根.
3.理解并运用a的双重非负性.
【过程与方法】
通过观察、理解开平方运算和平方运算之间的互逆关系,掌握求一个非负数的平方根和算术平方根的方法,培养学生的观察、演绎能力.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生的观察、归纳能力,通过合作学习体验成功的喜悦,激发学生学习数学的兴趣.
【教学重点】
能用符号正确表示一个数的平方根和算术平方根,理解开平方运算和平方运算之间的互逆关系,会求一个非负数的平方根和算术平方根.
【教学难点】
理解并运用a的双重非负数.
新课导入
思考:
1.我们现已学过哪些运算?
加、减、乘、除、乘方五种.
2.加法与减法这两种运算之间有什么关系?乘法与除法之间有什么关系?
互为逆运算
3.乘方有没有逆运算?
“卡西尼”号土星探测器历经了80多个月的飞行,成功进入环绕土星运行的轨道.要使土星探测器飞离地球,它的速度需大于v2.
上式中的v2如何计算?
进行新课
问题1
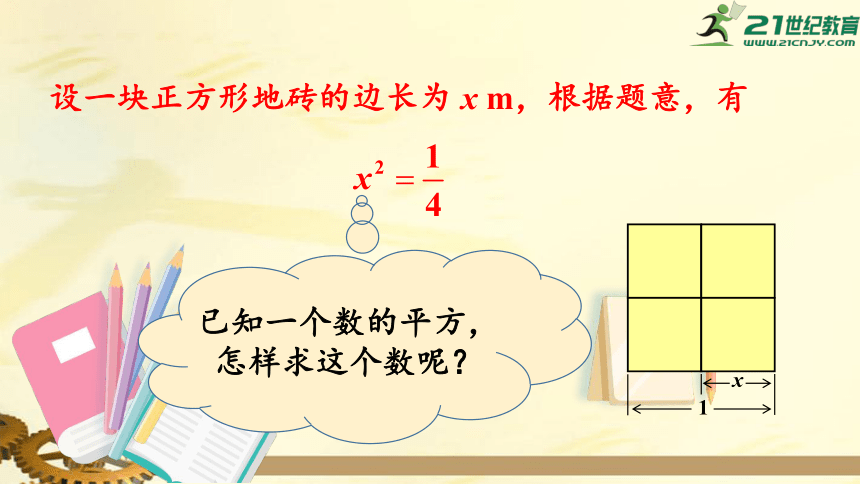
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1m2,如图,问这种地砖一块的边长是多少?
1
x
设一块正方形地砖的边长为
x
m,根据题意,有
已知一个数的平方,怎样求这个数呢?
1
x
思考与探索
1.一个数的平方是9,这个数是什么数?
2.一个数的平方是
,这个数是多少?
3.填空:
①(
)2
=
16
②(
)2
=
③(
)2
=
0
④(
)2
=
0.49
因为(±1.2)2=1.44
所以±1.2叫做1.44的平方根
因为(±2)2=4
所以±2叫做4的平方根
因为
x?
=
a
所以x叫做a的平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
概念引入
一个正数a的平方根有两个,它们互为相反数.我们用
表示其中正的平方根,读作“根号a”,另一个负的平方根记为﹣
.其中a叫做被开方数.
0的平方根是0;负数没有平方根.
例如,由于102=100,(
-10)2=100,所以100的平方根是+10和-10(可以合写为±10).
试一试:
请分别说出
49,
,0
的平方根.
解:因为(±7)2=49
所以±7叫做49的平方根.
因为(±
)2=
所以±
叫做
的平方根.
因为
02
=
0
所以0叫做0的平方根.
求一个数
a
的平方根的运算,叫做开平方.
平方运算与开平方运算互为逆运算.
+1
﹣1
+2
﹣2
+3
﹣3
1
4
9
1
4
9
+1
﹣1
+2
﹣2
+3
﹣3
开平方
平方
例1
判断下列各数是否有平方根,为什么?
25;
;0.016
9;﹣64.
解
因为正数和零都有平方根,负数没有平方根,所以25,
,0.016
9都有平方根;﹣64没有平方根.
平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
随堂练习
1.
4的平方根是(
)
A.16
B.2
C.±2
D.
2.
求下列各数的平方根.
(1)81;(2)
;(3)
;(4)0.49.
C
±9
±0.7
3.
判断下列说法是否正确.
①
的平方根是±16.
②
一定是正数.
③
若
,则a
=﹣5.
④
⑤
-6是(-6)2的平方根.
⑥
如果两个数平方后相等,那么它们也相等.
×
×
×
×
√
×
4.
若2m-4与3m-1是同一个正数的平方根,则m为(
)
A.﹣3
B.1
C.﹣1
D.﹣3或1
5.
若
是m的一个平方根,则m+13的平方根是_______.
D
±4
6.
已知
x-1
的平方根是±2,3x+y-1的平方根是±4,求3x+5y的平方根.
±5
课堂小结
平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
平方根的概念:
一个数的平方等于a,这个数叫做a的平方根.
课后作业
1.完成课本P5练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第6章
实
数
6.1
平方根、立方根
1.平方根
第1课时
平方根
沪科版·七年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握平方根、算术平方根的概念,明确平方根和算术平方根之间的联系和区别;
2.能用符号表示一个数的平方根和算术平方根,理解开平方运算和平方运算之间的互逆关系.会求一个非负数的平方根和算术平方根.
3.理解并运用a的双重非负性.
【过程与方法】
通过观察、理解开平方运算和平方运算之间的互逆关系,掌握求一个非负数的平方根和算术平方根的方法,培养学生的观察、演绎能力.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生的观察、归纳能力,通过合作学习体验成功的喜悦,激发学生学习数学的兴趣.
【教学重点】
能用符号正确表示一个数的平方根和算术平方根,理解开平方运算和平方运算之间的互逆关系,会求一个非负数的平方根和算术平方根.
【教学难点】
理解并运用a的双重非负数.
新课导入
思考:
1.我们现已学过哪些运算?
加、减、乘、除、乘方五种.
2.加法与减法这两种运算之间有什么关系?乘法与除法之间有什么关系?
互为逆运算
3.乘方有没有逆运算?
“卡西尼”号土星探测器历经了80多个月的飞行,成功进入环绕土星运行的轨道.要使土星探测器飞离地球,它的速度需大于v2.
上式中的v2如何计算?
进行新课
问题1
装修房屋,选用了某种型号的正方形地砖,这种地砖4块正好铺1m2,如图,问这种地砖一块的边长是多少?
1
x
设一块正方形地砖的边长为
x
m,根据题意,有
已知一个数的平方,怎样求这个数呢?
1
x
思考与探索
1.一个数的平方是9,这个数是什么数?
2.一个数的平方是
,这个数是多少?
3.填空:
①(
)2
=
16
②(
)2
=
③(
)2
=
0
④(
)2
=
0.49
因为(±1.2)2=1.44
所以±1.2叫做1.44的平方根
因为(±2)2=4
所以±2叫做4的平方根
因为
x?
=
a
所以x叫做a的平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
概念引入
一个正数a的平方根有两个,它们互为相反数.我们用
表示其中正的平方根,读作“根号a”,另一个负的平方根记为﹣
.其中a叫做被开方数.
0的平方根是0;负数没有平方根.
例如,由于102=100,(
-10)2=100,所以100的平方根是+10和-10(可以合写为±10).
试一试:
请分别说出
49,
,0
的平方根.
解:因为(±7)2=49
所以±7叫做49的平方根.
因为(±
)2=
所以±
叫做
的平方根.
因为
02
=
0
所以0叫做0的平方根.
求一个数
a
的平方根的运算,叫做开平方.
平方运算与开平方运算互为逆运算.
+1
﹣1
+2
﹣2
+3
﹣3
1
4
9
1
4
9
+1
﹣1
+2
﹣2
+3
﹣3
开平方
平方
例1
判断下列各数是否有平方根,为什么?
25;
;0.016
9;﹣64.
解
因为正数和零都有平方根,负数没有平方根,所以25,
,0.016
9都有平方根;﹣64没有平方根.
平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
随堂练习
1.
4的平方根是(
)
A.16
B.2
C.±2
D.
2.
求下列各数的平方根.
(1)81;(2)
;(3)
;(4)0.49.
C
±9
±0.7
3.
判断下列说法是否正确.
①
的平方根是±16.
②
一定是正数.
③
若
,则a
=﹣5.
④
⑤
-6是(-6)2的平方根.
⑥
如果两个数平方后相等,那么它们也相等.
×
×
×
×
√
×
4.
若2m-4与3m-1是同一个正数的平方根,则m为(
)
A.﹣3
B.1
C.﹣1
D.﹣3或1
5.
若
是m的一个平方根,则m+13的平方根是_______.
D
±4
6.
已知
x-1
的平方根是±2,3x+y-1的平方根是±4,求3x+5y的平方根.
±5
课堂小结
平方根的性质:
①一个正数有两个平方根,这两个平方根互为相反数;
②0只有一个平方根,它就是0本身;
③负数没有平方根.
平方根的概念:
一个数的平方等于a,这个数叫做a的平方根.
课后作业
1.完成课本P5练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
