1.1直角三角形的性质和判定(Ⅰ) 同步练习(含解析)
文档属性
| 名称 | 1.1直角三角形的性质和判定(Ⅰ) 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:09:17 | ||
图片预览





文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册1.1直角三角形的性质和判定(Ⅰ)
同步练习
一、单选题
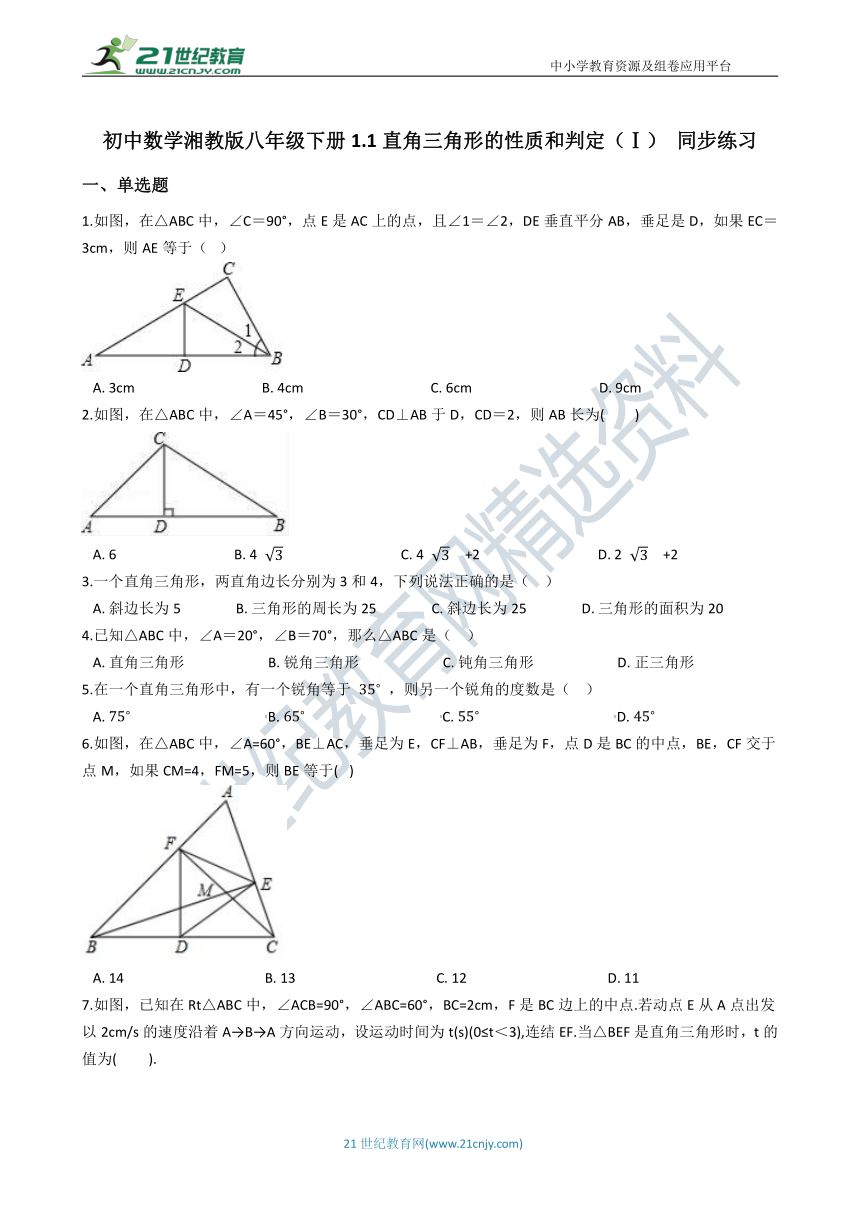
1.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于(?
)
A.?3cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?9cm
2.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB于D,CD=2,则AB长为( )
A.?6??????????????????????????????????B.?4
??????????????????????????????????C.?4
+2??????????????????????????????????D.?2
+2
3.一个直角三角形,两直角边长分别为3和4,下列说法正确的是(??
)
A.?斜边长为5????????????????B.?三角形的周长为25????????????????C.?斜边长为25????????????????D.?三角形的面积为20
4.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是(??
)
A.?直角三角形????????????????????????B.?锐角三角形????????????????????????C.?钝角三角形????????????????????????D.?正三角形
5.在一个直角三角形中,有一个锐角等于
,则另一个锐角的度数是(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于(?
)
A.?14?????????????????????????????????????????B.?13?????????????????????????????????????????C.?12?????????????????????????????????????????D.?11
7.如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为(???????
).
A.?????????????????????????????????B.?1????????????????????????????????C.?
或1或
????????????????????????????????D.?
或1或
8.如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是(???
)
A.?
m??????????????????????????????????B.?4m??????????????????????????????????C.?4
m??????????????????????????????????D.?8m
9.△ABC中,∠A:∠B:∠C=1:2:3,最小边BC=4
cm,最长边AB的长是(??
)
A.?5cm?????????????????????????????????????B.?6cm?????????????????????????????????????C.?7cm?????????????????????????????????????D.?8cm
10.下列关于直角三角形的说法中错误的是(??
)
A.?直角三角形的两个锐角互余?????????????????????????B.?直角三角形斜边的中点到三个顶点的距离相等
C.?直角三角形斜边上的高等于斜边的一半???????D.?直角三角形中有两条边的平方和等于第三条边的平方
二、填空题
11.如果直角三角形的一个内角为40°,则这个直角三角形的另一个锐角为________.
12.已知,如图,△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC=________cm.
13.如图,矩形
ABCD
的对角线
AC
与
BD
相交于点
O,∠ADB=30°,AB=4,则
AD=________.
14.等腰三角形腰上的高等于腰长的一半,则这个等腰三角形的顶角为________度.
三、解答题
15.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
16.如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由。
?
17.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.
四、综合题
18.清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S
,
则第一步:
=m;第二步:
=k;第三步:分别用3、4、5乘以k
,
得三边长”.
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的符合题意性吗?请写出证明过程.
19.如图,已知∠ACB=90°,CD是AB上的高,∠A=30°,AB=4cm,则:
(1)BC=________;
(2)∠BCD=________;
(3)BD=________;
(4)AD=________.
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠2=∠A,
∵∠1=∠2,
∴∠A=∠1=∠2,
∵∠C=90°,
∴∠A=∠1=∠2=30°,
∵∠1=∠2,ED⊥AB,∠C=90°,
∴CE=DE=3cm,
在Rt△ADE中,∠ADE=90°,∠A=30°,
∴AE=2DE=6cm,
故答案为:C.
【分析】求出AE=BE,推出∠A=∠1=∠2=30°,求出DE=CE=3cm,根据含30度角的直角三角形性质求出即可.
2.【答案】
D
【解析】【解答】在Rt△ACD中,∠A=45°,CD=2,
则AD=CD=2,
在Rt△CDB中,∠B=30°,CD=2,
则BD=2
,
故AB=AD+BD=2
+2.
故答案为:D.
【分析】在Rt△ACD中求出AD,在Rt△CDB中求出BD,继而可得出AB.
3.【答案】
A
【解析】【解答】有勾股定理得:斜边=
=5,故A符合题意,C不符合题意;
三角形的周长为:3+4+5=12,故B不符合题意;
三角形的面积为:
×3×4=6,故D不符合题意.
故答案为:A.
【分析】结合勾股定理,三角形的面积以及周长公式进行计算即可。
4.【答案】
A
【解析】【解答】解:∵△ABC中,∠A=20°,∠B=70°,
∴∠C=180°-20°-70°=90°,
∴△ABC是直角三角形.
故答案为:A.
【分析】根据三角形的内角和定理可知,第三个角的度数为90°,即可判断三角形为直角三角形。
5.【答案】
C
【解析】【解答】解:
在一个直角三角形中,有一个锐角等于
,
另一个锐角的度数是
.
故答案为:C.
【分析】利用直角三角形两锐角互余解答即可.
6.【答案】
C
【解析】【解答】解:∵
BE⊥AC,
CF⊥AB,
∴∠AEB=∠AFC=90°,
∵
∠A=60°,
∴∠ABE=∠ACF=30°,
在Rt△FBM中,
∵
FM=5,
∴BM=2FM=10,
在Rt△EMC中,
∵
CM=4,
∴EM=CM=2,
∴BE=BM+ME=10+2=12.
故答案为:C.
【分析】根据垂直的定义可知∠AEB=∠AFC=90°,由三角形内角和定理得∠ABE=∠ACF=30°,在Rt△FBM、Rt△EMC中,根据直角三角形的性质求得BM=10,EM=2,再由BE=BM+ME即可求得答案.
7.【答案】
C
【解析】【解答】解:在Rt△ABC中,∵∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm.
∵F是AB的中点,
∴BF=AF=
cm.
①当EF⊥BC时,∵∠ABC=60°,
∴∠BEF=30°,
∴BE=2BF=2,
∴AE=AB-BE=4-2=2,
∴t=2÷2=1或t=(4+2)÷2=3(舍);
②当EF⊥AB时,∵∠ABC=60°,
∴∠BFE=30°,
∴BE=
BF=
,
∴AE=AB-BE=4-
=
,
∴t=
÷2=
或t=(4+
)÷2=
?(舍);
故答案为:C.
【分析】△BEF是直角三角形时,而△BEF中∠ABC=60°,故有EF⊥BC和EF⊥AB这两种情况,由直角三角形30°所对的直角边是斜边的一半,求出BE的长,则可求出E所运动的距离,注意点E是运动路线是A→B→A,且t(s)(0≤t<3).
8.【答案】
B
【解析】【解答】解:过C作CM⊥AB于M,
则CM=h,∠CMB=90°,
∵∠ABC=150°,
∴∠CBM=30°,
∴h=CM=
BC=4m,
故答案为:B.
【分析】先添加辅助线过C作垂线,构造直角三角形,根据外角150°可得∠CBM的度数,再根据直角三角形的性质得出h的高度.
9.【答案】
D
【解析】【解答】设∠A=x°,∠B=2x°,∠C=3x°
故x°+2x°+3x°=180°
∴x=30°
∴∠A=30°,∠C=90°,
∴AB=2BC=8,故答案为:D
【分析】根据三个内角的比以及三角形的内角和定理,得直角三角形中的最小内角是30°,根据30°所对的直角边是斜边的一半,得最长边是最小边的2倍,从而得出答案。
10.【答案】
C
【解析】【解答】A选项:直角三角形的两个锐角互余,A不符合题意;
B选项:直角三角形斜边的中点到三个顶点的距离相等,B不符合题意;
C选项:直角三角形斜边上的中线等于斜边的一半,C符合题意;
D选项:直角三角形中有两条边的平方和等于第三条边的平方,D不符合题意;
故答案为:C.
【分析】根据直角三角形的性质判断即可。
二、填空题
11.【答案】
50°
【解析】【解答】∵直角三角形的一个内角为40°,
∴这个直角三角形的另一个锐角=90°﹣40°=50°,
故答案为50°.
【分析】根据直角三角形两锐角互余进行求解即可.
12.【答案】
3
【解析】【解答】解:因为在△ABC中,∠C=90°,∠A=30°,AB=6cm,
可得:BC=3cm,
故答案为:3.
【分析】在直角三角形中,如果有一个角等于30°,那么这个角所对的直角边等于斜边的一半。
13.【答案】
4
【解析】【解答】∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ADB=30°,
∴BD=2AB=8,
∴AD2=BD2-AB2
,
∴AD2=64-16=48
∴AD=4
故答案为:4
【分析】由30°的角所对的边等于斜边的一半求出BD=8,再由勾股定理求出AD的长即可.
14.【答案】
30或150
【解析】【解答】①如图,
∵BD是△ABC的高,AB=AC,BD=
AB,
∴∠A=30°,
②如图,
∵CD是△ABC边BA
上的高,DC=?
AC,
∴∠DAC=30°,
∴∠BAC=180°-30°=150°,
故答案为:30或150
【分析】此题分两种情况:①如图,根据含30°直角三角形的边之间的关系的逆用,由BD是△ABC的高,AB=AC,BD=?AB,得出∠A=30°;②如图,根据含30°直角三角形的边之间的关系的逆用,由CD是△ABC边BA
上的高,DC=?
AC,得出∠DAC=30°,根据邻补角的定义算出∠BAC,从而得出答案。
三、解答题
15.【答案】
解:在Rt△ABF中,∠A=70,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
【解析】【分析】在Rt△ABF中,∠A=70,CE,BF是两条高,求得∠EBF的度数,在Rt△BCF中∠FBC=40°求得∠FBC的度数
16.【答案】
解:连接AP,且做PD垂直于AB交AB延长线于D点,
∵∠PBC=30°
∴∠PBA=150°
又∵∠A=15°
∴∠APB=15°
∴PB=PA=45×3=45海里
∴PD=22.5海里(30度角所对的边等于斜边一半)
【解析】【分析】先添加辅助线过P作垂线构造直角三角形,根据∠PBC的度数可得∠PBA,再根据∠A的度数可得∠APB的度数,从而可得PB的长度,最后根据直角三角形中特殊角的性质可得PD.
17.【答案】
解:如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠CPO,
∴∠PCE=∠BOP+∠CPO=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=PC=×4=2,
∵AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
【解析】【分析】过点P作PE⊥OB于E,根据两直线平行,内错角相等可得∠AOP=∠CPO,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半解答.
四、综合题
18.【答案】
(1)解:当s=150时,m=
=25,k=
=5.
∴3×5=15,4×5=20,5×5=25,
∴直角三角形的三边长分别为15,20,25
(2)解:符合题意,设直角三角形的三边长分别为3k,4k,5k,
∴s=
×3k×4k=6k?,
∴k=
,
∴三边长分别为3
,4
,5
【解析】【分析】(1)按照题目所给的步骤即可求出三边的长。
(2)用反证法进行证明,根据题意设三边长分别为3k、4k、5k,计算出s与k的关系,再用s表示三边即可对该方法进行验证。
19.【答案】
(1)2cm
(2)30°
(3)1cm
(4)3cm
【解析】【解答】解:(1)∵∠ACB=90°,∠A=30°,AB=4cm,
∴BC=
AB=
×4=2cm;(2)∵CD是AB上的高,
∴∠BCD+∠B=90°,
又∵∠A+∠B=90°,
∴∠BCD=∠A=30°;(3)在Rt△BCD中,BD=
BC=
×2=1cm;(4)AD=AB﹣BD=4﹣1=3cm.
故答案为:2cm,30°,1cm,3cm.
【分析】(1)根据直角三角形30°角所对的直角边等于斜边的一半可得BC=
AB(2)根据同角的余角相等可得∠BCD=∠A;(3)根据直角三角形30°角所对的直角边等于斜边的一半可得BD=
BC;(4)根据AD=AB﹣BD代入数据计算即可得解.
(
第
一
页
共
1
页
)
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册1.1直角三角形的性质和判定(Ⅰ)
同步练习
一、单选题
1.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于(?
)
A.?3cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?9cm
2.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB于D,CD=2,则AB长为( )
A.?6??????????????????????????????????B.?4
??????????????????????????????????C.?4
+2??????????????????????????????????D.?2
+2
3.一个直角三角形,两直角边长分别为3和4,下列说法正确的是(??
)
A.?斜边长为5????????????????B.?三角形的周长为25????????????????C.?斜边长为25????????????????D.?三角形的面积为20
4.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是(??
)
A.?直角三角形????????????????????????B.?锐角三角形????????????????????????C.?钝角三角形????????????????????????D.?正三角形
5.在一个直角三角形中,有一个锐角等于
,则另一个锐角的度数是(??
)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
6.如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于(?
)
A.?14?????????????????????????????????????????B.?13?????????????????????????????????????????C.?12?????????????????????????????????????????D.?11
7.如图,已知在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连结EF.当△BEF是直角三角形时,t的值为(???????
).
A.?????????????????????????????????B.?1????????????????????????????????C.?
或1或
????????????????????????????????D.?
或1或
8.如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是(???
)
A.?
m??????????????????????????????????B.?4m??????????????????????????????????C.?4
m??????????????????????????????????D.?8m
9.△ABC中,∠A:∠B:∠C=1:2:3,最小边BC=4
cm,最长边AB的长是(??
)
A.?5cm?????????????????????????????????????B.?6cm?????????????????????????????????????C.?7cm?????????????????????????????????????D.?8cm
10.下列关于直角三角形的说法中错误的是(??
)
A.?直角三角形的两个锐角互余?????????????????????????B.?直角三角形斜边的中点到三个顶点的距离相等
C.?直角三角形斜边上的高等于斜边的一半???????D.?直角三角形中有两条边的平方和等于第三条边的平方
二、填空题
11.如果直角三角形的一个内角为40°,则这个直角三角形的另一个锐角为________.
12.已知,如图,△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC=________cm.
13.如图,矩形
ABCD
的对角线
AC
与
BD
相交于点
O,∠ADB=30°,AB=4,则
AD=________.
14.等腰三角形腰上的高等于腰长的一半,则这个等腰三角形的顶角为________度.
三、解答题
15.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
16.如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,3小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由。
?
17.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.
四、综合题
18.清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日,西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,设其面积为S
,
则第一步:
=m;第二步:
=k;第三步:分别用3、4、5乘以k
,
得三边长”.
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的符合题意性吗?请写出证明过程.
19.如图,已知∠ACB=90°,CD是AB上的高,∠A=30°,AB=4cm,则:
(1)BC=________;
(2)∠BCD=________;
(3)BD=________;
(4)AD=________.
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠2=∠A,
∵∠1=∠2,
∴∠A=∠1=∠2,
∵∠C=90°,
∴∠A=∠1=∠2=30°,
∵∠1=∠2,ED⊥AB,∠C=90°,
∴CE=DE=3cm,
在Rt△ADE中,∠ADE=90°,∠A=30°,
∴AE=2DE=6cm,
故答案为:C.
【分析】求出AE=BE,推出∠A=∠1=∠2=30°,求出DE=CE=3cm,根据含30度角的直角三角形性质求出即可.
2.【答案】
D
【解析】【解答】在Rt△ACD中,∠A=45°,CD=2,
则AD=CD=2,
在Rt△CDB中,∠B=30°,CD=2,
则BD=2
,
故AB=AD+BD=2
+2.
故答案为:D.
【分析】在Rt△ACD中求出AD,在Rt△CDB中求出BD,继而可得出AB.
3.【答案】
A
【解析】【解答】有勾股定理得:斜边=
=5,故A符合题意,C不符合题意;
三角形的周长为:3+4+5=12,故B不符合题意;
三角形的面积为:
×3×4=6,故D不符合题意.
故答案为:A.
【分析】结合勾股定理,三角形的面积以及周长公式进行计算即可。
4.【答案】
A
【解析】【解答】解:∵△ABC中,∠A=20°,∠B=70°,
∴∠C=180°-20°-70°=90°,
∴△ABC是直角三角形.
故答案为:A.
【分析】根据三角形的内角和定理可知,第三个角的度数为90°,即可判断三角形为直角三角形。
5.【答案】
C
【解析】【解答】解:
在一个直角三角形中,有一个锐角等于
,
另一个锐角的度数是
.
故答案为:C.
【分析】利用直角三角形两锐角互余解答即可.
6.【答案】
C
【解析】【解答】解:∵
BE⊥AC,
CF⊥AB,
∴∠AEB=∠AFC=90°,
∵
∠A=60°,
∴∠ABE=∠ACF=30°,
在Rt△FBM中,
∵
FM=5,
∴BM=2FM=10,
在Rt△EMC中,
∵
CM=4,
∴EM=CM=2,
∴BE=BM+ME=10+2=12.
故答案为:C.
【分析】根据垂直的定义可知∠AEB=∠AFC=90°,由三角形内角和定理得∠ABE=∠ACF=30°,在Rt△FBM、Rt△EMC中,根据直角三角形的性质求得BM=10,EM=2,再由BE=BM+ME即可求得答案.
7.【答案】
C
【解析】【解答】解:在Rt△ABC中,∵∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm.
∵F是AB的中点,
∴BF=AF=
cm.
①当EF⊥BC时,∵∠ABC=60°,
∴∠BEF=30°,
∴BE=2BF=2,
∴AE=AB-BE=4-2=2,
∴t=2÷2=1或t=(4+2)÷2=3(舍);
②当EF⊥AB时,∵∠ABC=60°,
∴∠BFE=30°,
∴BE=
BF=
,
∴AE=AB-BE=4-
=
,
∴t=
÷2=
或t=(4+
)÷2=
?(舍);
故答案为:C.
【分析】△BEF是直角三角形时,而△BEF中∠ABC=60°,故有EF⊥BC和EF⊥AB这两种情况,由直角三角形30°所对的直角边是斜边的一半,求出BE的长,则可求出E所运动的距离,注意点E是运动路线是A→B→A,且t(s)(0≤t<3).
8.【答案】
B
【解析】【解答】解:过C作CM⊥AB于M,
则CM=h,∠CMB=90°,
∵∠ABC=150°,
∴∠CBM=30°,
∴h=CM=
BC=4m,
故答案为:B.
【分析】先添加辅助线过C作垂线,构造直角三角形,根据外角150°可得∠CBM的度数,再根据直角三角形的性质得出h的高度.
9.【答案】
D
【解析】【解答】设∠A=x°,∠B=2x°,∠C=3x°
故x°+2x°+3x°=180°
∴x=30°
∴∠A=30°,∠C=90°,
∴AB=2BC=8,故答案为:D
【分析】根据三个内角的比以及三角形的内角和定理,得直角三角形中的最小内角是30°,根据30°所对的直角边是斜边的一半,得最长边是最小边的2倍,从而得出答案。
10.【答案】
C
【解析】【解答】A选项:直角三角形的两个锐角互余,A不符合题意;
B选项:直角三角形斜边的中点到三个顶点的距离相等,B不符合题意;
C选项:直角三角形斜边上的中线等于斜边的一半,C符合题意;
D选项:直角三角形中有两条边的平方和等于第三条边的平方,D不符合题意;
故答案为:C.
【分析】根据直角三角形的性质判断即可。
二、填空题
11.【答案】
50°
【解析】【解答】∵直角三角形的一个内角为40°,
∴这个直角三角形的另一个锐角=90°﹣40°=50°,
故答案为50°.
【分析】根据直角三角形两锐角互余进行求解即可.
12.【答案】
3
【解析】【解答】解:因为在△ABC中,∠C=90°,∠A=30°,AB=6cm,
可得:BC=3cm,
故答案为:3.
【分析】在直角三角形中,如果有一个角等于30°,那么这个角所对的直角边等于斜边的一半。
13.【答案】
4
【解析】【解答】∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ADB=30°,
∴BD=2AB=8,
∴AD2=BD2-AB2
,
∴AD2=64-16=48
∴AD=4
故答案为:4
【分析】由30°的角所对的边等于斜边的一半求出BD=8,再由勾股定理求出AD的长即可.
14.【答案】
30或150
【解析】【解答】①如图,
∵BD是△ABC的高,AB=AC,BD=
AB,
∴∠A=30°,
②如图,
∵CD是△ABC边BA
上的高,DC=?
AC,
∴∠DAC=30°,
∴∠BAC=180°-30°=150°,
故答案为:30或150
【分析】此题分两种情况:①如图,根据含30°直角三角形的边之间的关系的逆用,由BD是△ABC的高,AB=AC,BD=?AB,得出∠A=30°;②如图,根据含30°直角三角形的边之间的关系的逆用,由CD是△ABC边BA
上的高,DC=?
AC,得出∠DAC=30°,根据邻补角的定义算出∠BAC,从而得出答案。
三、解答题
15.【答案】
解:在Rt△ABF中,∠A=70,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
【解析】【分析】在Rt△ABF中,∠A=70,CE,BF是两条高,求得∠EBF的度数,在Rt△BCF中∠FBC=40°求得∠FBC的度数
16.【答案】
解:连接AP,且做PD垂直于AB交AB延长线于D点,
∵∠PBC=30°
∴∠PBA=150°
又∵∠A=15°
∴∠APB=15°
∴PB=PA=45×3=45海里
∴PD=22.5海里(30度角所对的边等于斜边一半)
【解析】【分析】先添加辅助线过P作垂线构造直角三角形,根据∠PBC的度数可得∠PBA,再根据∠A的度数可得∠APB的度数,从而可得PB的长度,最后根据直角三角形中特殊角的性质可得PD.
17.【答案】
解:如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠CPO,
∴∠PCE=∠BOP+∠CPO=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=PC=×4=2,
∵AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
【解析】【分析】过点P作PE⊥OB于E,根据两直线平行,内错角相等可得∠AOP=∠CPO,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半解答.
四、综合题
18.【答案】
(1)解:当s=150时,m=
=25,k=
=5.
∴3×5=15,4×5=20,5×5=25,
∴直角三角形的三边长分别为15,20,25
(2)解:符合题意,设直角三角形的三边长分别为3k,4k,5k,
∴s=
×3k×4k=6k?,
∴k=
,
∴三边长分别为3
,4
,5
【解析】【分析】(1)按照题目所给的步骤即可求出三边的长。
(2)用反证法进行证明,根据题意设三边长分别为3k、4k、5k,计算出s与k的关系,再用s表示三边即可对该方法进行验证。
19.【答案】
(1)2cm
(2)30°
(3)1cm
(4)3cm
【解析】【解答】解:(1)∵∠ACB=90°,∠A=30°,AB=4cm,
∴BC=
AB=
×4=2cm;(2)∵CD是AB上的高,
∴∠BCD+∠B=90°,
又∵∠A+∠B=90°,
∴∠BCD=∠A=30°;(3)在Rt△BCD中,BD=
BC=
×2=1cm;(4)AD=AB﹣BD=4﹣1=3cm.
故答案为:2cm,30°,1cm,3cm.
【分析】(1)根据直角三角形30°角所对的直角边等于斜边的一半可得BC=
AB(2)根据同角的余角相等可得∠BCD=∠A;(3)根据直角三角形30°角所对的直角边等于斜边的一半可得BD=
BC;(4)根据AD=AB﹣BD代入数据计算即可得解.
(
第
一
页
共
1
页
)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
