第2章 相交线与平行线检测题1(含答案)
文档属性
| 名称 | 第2章 相交线与平行线检测题1(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 457.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 08:31:05 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期七年级数学(下册)
第2章相交线与平行线检测题1(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、在同一平面内,不重合的两条直线的位置关系为(
)
A.平行
B.相交
C.平行或相交
D.平行或相交或垂直
2、在同一平面内,若a∥c,c⊥b则a与b的位置关系是(
)
A.平行
B.垂直
C.相交
D.重合
3、如图,若l1∥l2,则下列选项中不一定成立的是( )
A.∠1=∠5
B.∠2=∠3
C.∠1=∠3
D.∠1+∠4=180°
4、把含有30°直角三角板和直尺如图放置,若∠1=27°,则∠2的度数为( )
A.43°
B.33°
C.32°
D.31°
5、若点P为直线l外一点,点A、B、C为直线l上的不同的点,其中PA=5,PB=6,PC=6.5,那么点P到直线l的距离是( )
A.小于5
B.等于5
C.大于或等于5
D.小于或等于5
6、如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3等于(??
)
A.90°???????????????????????????B.120°????????????????
??????????C.180°?
??????????????????????D.360°
7.一个角的补角与这个的余角的差是(??
)
A.直角????????????????
??????????B.锐角???????????
?????????C.钝角????????
????????????D.不能确定
8、如图,已知∠AOB,由如下作法可以得到的结论是(
)
(1)作射线;(2)以O为圆心,以任意长为半径作弧,交OA于点C,交OB与D;(3)
以为
圆心,以OC长为半径作弧,交于点;(4)
以为圆心,以CD长为半径作弧,交前面
的弧于点;(5)过点作射线,得到∠AOB.则∠与的大小关系为(
)
A.∠AOB>???????B.∠AOB>?
C.∠AOB=???????????D.无法确定
9、已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且只有一条?????????????????B.有无数条????????????????????C.不存在???????????????D.有一条或不存在
10、下列说法:①如果两个角相等,那么这两个角是对顶角;②过直线外一点,有且只有一条直线平行于已知直线;③与一个已知点P的距离等于5cm的直线有且只有一条;④若∠1+∠2+∠3=90°,则∠1、∠2、∠3互为余角;;⑤若两条直线都和第三条直线平行,则这两条直线平行.正确的个数有( )个.
A.4??????????????????
??????B.3???????????????????
???????C.2?????????????
??????????D.1
二、填空题
(每题3分,共30分)
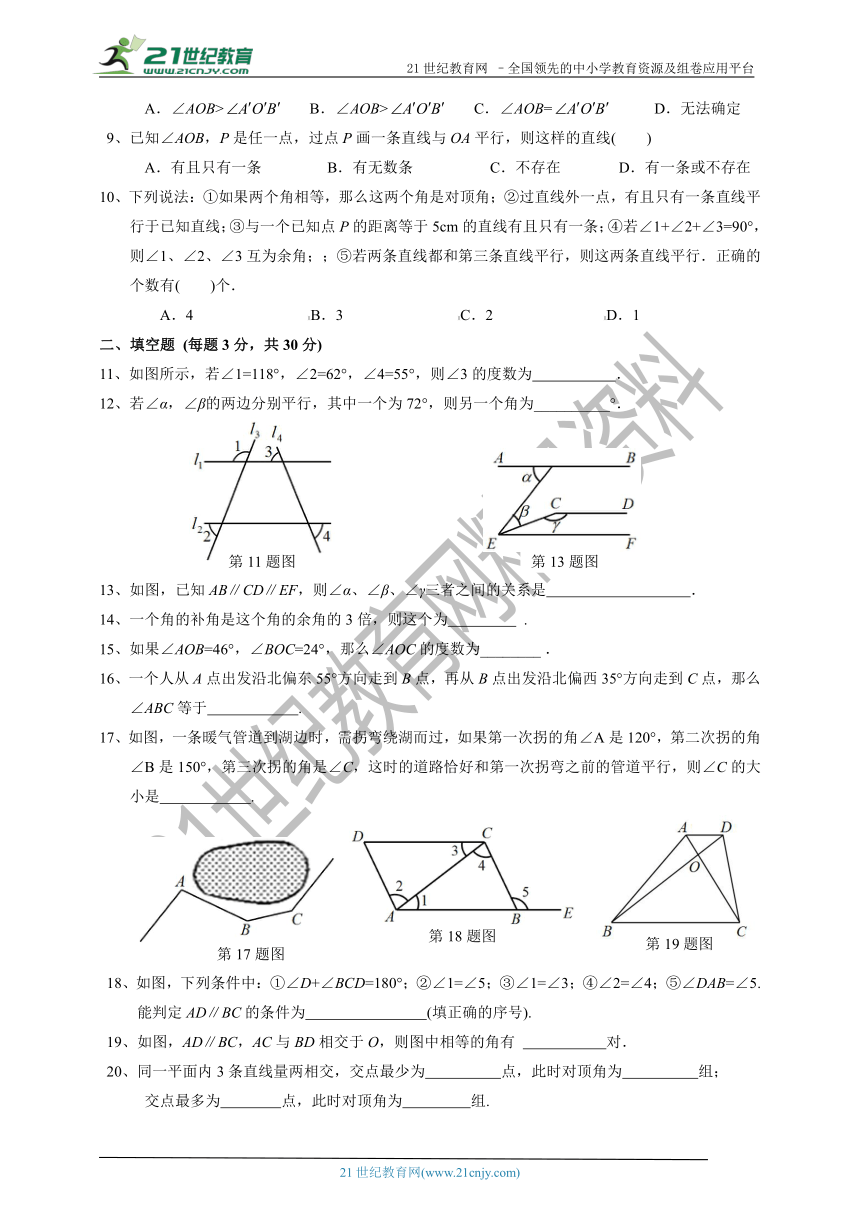
11、如图所示,若∠1=118°,∠2=62°,∠4=55°,则∠3的度数为
.
12、若∠α,∠β的两边分别平行,其中一个为72°,则另一个角为__________°.
13、如图,已知AB∥CD∥EF,则∠α、∠β、∠γ三者之间的关系是
.
14、一个角的补角是这个角的余角的3倍,则这个为
.
15、如果∠AOB=46°,∠BOC=24°,那么∠AOC的度数为________?.
16、一个人从A点出发沿北偏东55°方向走到B点,再从B点出发沿北偏西35°方向走到C点,那么∠ABC等于
.
17、如图,一条暖气管道到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的管道平行,则∠C的大小是
.
18、如图,下列条件中:①∠D+∠BCD=180°;②∠1=∠5;③∠1=∠3;④∠2=∠4;⑤∠DAB=∠5.能判定AD∥BC的条件为
(填正确的序号).
19、如图,AD∥BC,AC与BD相交于O,则图中相等的角有
对.
20、同一平面内3条直线量两相交,交点最少为
点,此时对顶角为
组;
交点最多为
点,此时对顶角为
组.
三、解答题(共6题
共60分)
21、(8分)
如图,AB∥CD,EF分别交AB、CD于点M、N,∠1=48°,MG平分∠BMF,MG
交CD于G,求∠2的度数.
解:∵∠1=48°(
),
∴∠BMF=
(
).
∵MG平分∠BMF
,
∴∠BMG=
=
(
).
∵AB∥CD(
),
∴∠2=
=
(
).
22、(12分)
如图,直线AB、CD、EF相交于点O.
(1)若∠1=21°,∠2=32°,求∠3的度数;
(2)
若9∠2=2∠3,∠1=26°,求∠AOF的度数;
(3)
若∠3-∠2=96°,∠1=20°,求∠EOB的度数;
23、(10分)
如图,已知∠A+∠APC+∠C=360°,试说明:AB∥CD.
24、(10分)动手画一画在同一平面内有12条直线,最少把平面分成几部分?最多分成几部分?
25、(9分)
已知:如图,BC⊥DC,BE平分∠ABC,AE平分∠BAD,∠1+∠2=90°,探究:DA与DC的位置关系.
26、(11分)如图(1),将两块直角三角尺的直角顶点C叠放在一起;
(1)若∠DCE=32°,∠ACB=______;若∠ACB=145°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE
的大小又有何关系,请说明理由.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
B
D
C
A
C
D
C
二、填空题(共10小题
每题3分
共30分)
11、55°
12、72或108
13、∠α+∠γ-∠β=180°
14、45°
15、70°或22°
16、90°
17、150°
18、①④⑤
19、4
20、1,5;3,6.
三、解答题(共6题
共60分)
21、(8分)
如图,AB∥CD,EF分别交AB、CD于点M、N,∠1=48°,MG平分∠BMF,MG
交CD于G,求∠2的度数.
解:∵∠1=48°(
已知
),
∴∠BMF=
132°
(
邻补角定义
).
∵MG平分∠BMF
,
∴∠BMG=
∠BMF
=
66°
(
角平分线定义
).
∵AB∥CD(
已知
),
∴∠2=
∠BMG
=
66°
(
两直线平行内错角
).
22、(12分)
如图,直线AB、CD、EF相交于点O.
(1)若∠1=21°,∠2=32°,求∠3的度数;
(2)
若9∠2=2∠3,∠1=26°,求∠AOF的度数;
(3)
若∠3-∠2=96°,∠1=20°,求∠EOB的度数;
解:(1)∵直线AB、CD、EF相交于点O.
∴∠1=∠DOF=21°,∠2=∠AOE=32°,
∵∠AOE+∠3+∠DOF=180°,
∴∠3=127°.
(2)设∠2=x°,则∠3=x°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+x+26=180.
解得x=28°,x°=126°.
∴∠2=28°,∠3=126°.
∴∠AOF=∠AOD+∠DOF=∠3+∠1=152°.
(3)设∠2=x°,则∠3=x°+96°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+
x+96+20=180.
解得x=32°,x°+96°=128°.
∴∠2=32°,∠3=128°.
∴∠EOB=∠1+∠COB=∠1+∠3=20°+128°=148°.
23、(10分)
如图,已知∠A+∠APC+∠C=360°,试说明:AB∥CD.
解:如答题图,过点P作PE∥AB,
∵PE∥AB,
∴∠A+∠1=180°.
∵∠APC=∠1+∠2,∠A+∠APC+∠C=360°,
∴∠A+∠1+∠2+∠C=360°.
∴∠2+∠C=180°.
∴PE∥CD.
∴AB∥CD.
24、(10分)动手画一画在同一平面内有12条直线,最少把平面分成几部分?最多分成几部分?
解:(1)有一条直线时,最少分成2部分,最多分成1+1=2部分;
(2)有两条直线时,最少分成4部分,最多分成1+1+2=4部分;
(3)有三条直线时,最少分成6部分,最多分成1+1+2+3=7部分;
(4)设直线条数有n条,分成的平面最多有a个,最少有b个,有以下规律:
m=1+1+2+3+…+(n-1)+n=,b=2n;
所以平面内有12条直线最多可将平面分成=79部分,最少2×12=24部分.
25、(9分)
已知:如图,BC⊥DC,BE平分∠ABC,AE平分∠BAD,∠1+∠2=90°,探究:DA与DC的位置关系.
解:∵AE平分∠BAD,BE平分∠ABC,
∴∠BAD=2∠1,∠ABC=2∠2
∴∠BAD+∠ABC=2∠1+2∠2=2(∠1+∠2),
∵∠1+∠2=90°,
∴∠BAD+∠ABC=2∠1+2∠2=2×90°=180°,
∴AD∥BC,
∴∠D+∠C=180°,
∵BC⊥DC,,
∴∠C=90°,
∴∠D=90°
∴DA⊥DC.
26、(11分)如图(1),将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=32°,∠ACB=______;若∠ACB=145°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE
的大小又有何关系,请说明理由.
(1)∵∠ECB=90°,∠DCE=32°
∴∠DCB=90°-32°=58°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=148°,
∵∠ACB=145°,∠ACD=90°
∴∠DCB=145°-90°=55°
∵∠ECB=90°
∴∠DCE=90°-55°=35°,
故答案为:148°,35°
(2)猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°.
(3)∠DAB+∠CAE=120°
理由如下:由于∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
第23题图(1)
第18题图
第4题图
第11题图
第26题图(2)
第25题图
第23题图
第23题图
第22题图
第3题图
第6题图
第21题图
第25题图
第23题图
第26题图(2)
第22题图
第21题图
第13题图
第19题图
第23题图(1)
第17题图
第6题图
第6题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期七年级数学(下册)
第2章相交线与平行线检测题1(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、在同一平面内,不重合的两条直线的位置关系为(
)
A.平行
B.相交
C.平行或相交
D.平行或相交或垂直
2、在同一平面内,若a∥c,c⊥b则a与b的位置关系是(
)
A.平行
B.垂直
C.相交
D.重合
3、如图,若l1∥l2,则下列选项中不一定成立的是( )
A.∠1=∠5
B.∠2=∠3
C.∠1=∠3
D.∠1+∠4=180°
4、把含有30°直角三角板和直尺如图放置,若∠1=27°,则∠2的度数为( )
A.43°
B.33°
C.32°
D.31°
5、若点P为直线l外一点,点A、B、C为直线l上的不同的点,其中PA=5,PB=6,PC=6.5,那么点P到直线l的距离是( )
A.小于5
B.等于5
C.大于或等于5
D.小于或等于5
6、如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3等于(??
)
A.90°???????????????????????????B.120°????????????????
??????????C.180°?
??????????????????????D.360°
7.一个角的补角与这个的余角的差是(??
)
A.直角????????????????
??????????B.锐角???????????
?????????C.钝角????????
????????????D.不能确定
8、如图,已知∠AOB,由如下作法可以得到的结论是(
)
(1)作射线;(2)以O为圆心,以任意长为半径作弧,交OA于点C,交OB与D;(3)
以为
圆心,以OC长为半径作弧,交于点;(4)
以为圆心,以CD长为半径作弧,交前面
的弧于点;(5)过点作射线,得到∠AOB.则∠与的大小关系为(
)
A.∠AOB>???????B.∠AOB>?
C.∠AOB=???????????D.无法确定
9、已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且只有一条?????????????????B.有无数条????????????????????C.不存在???????????????D.有一条或不存在
10、下列说法:①如果两个角相等,那么这两个角是对顶角;②过直线外一点,有且只有一条直线平行于已知直线;③与一个已知点P的距离等于5cm的直线有且只有一条;④若∠1+∠2+∠3=90°,则∠1、∠2、∠3互为余角;;⑤若两条直线都和第三条直线平行,则这两条直线平行.正确的个数有( )个.
A.4??????????????????
??????B.3???????????????????
???????C.2?????????????
??????????D.1
二、填空题
(每题3分,共30分)
11、如图所示,若∠1=118°,∠2=62°,∠4=55°,则∠3的度数为
.
12、若∠α,∠β的两边分别平行,其中一个为72°,则另一个角为__________°.
13、如图,已知AB∥CD∥EF,则∠α、∠β、∠γ三者之间的关系是
.
14、一个角的补角是这个角的余角的3倍,则这个为
.
15、如果∠AOB=46°,∠BOC=24°,那么∠AOC的度数为________?.
16、一个人从A点出发沿北偏东55°方向走到B点,再从B点出发沿北偏西35°方向走到C点,那么∠ABC等于
.
17、如图,一条暖气管道到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的管道平行,则∠C的大小是
.
18、如图,下列条件中:①∠D+∠BCD=180°;②∠1=∠5;③∠1=∠3;④∠2=∠4;⑤∠DAB=∠5.能判定AD∥BC的条件为
(填正确的序号).
19、如图,AD∥BC,AC与BD相交于O,则图中相等的角有
对.
20、同一平面内3条直线量两相交,交点最少为
点,此时对顶角为
组;
交点最多为
点,此时对顶角为
组.
三、解答题(共6题
共60分)
21、(8分)
如图,AB∥CD,EF分别交AB、CD于点M、N,∠1=48°,MG平分∠BMF,MG
交CD于G,求∠2的度数.
解:∵∠1=48°(
),
∴∠BMF=
(
).
∵MG平分∠BMF
,
∴∠BMG=
=
(
).
∵AB∥CD(
),
∴∠2=
=
(
).
22、(12分)
如图,直线AB、CD、EF相交于点O.
(1)若∠1=21°,∠2=32°,求∠3的度数;
(2)
若9∠2=2∠3,∠1=26°,求∠AOF的度数;
(3)
若∠3-∠2=96°,∠1=20°,求∠EOB的度数;
23、(10分)
如图,已知∠A+∠APC+∠C=360°,试说明:AB∥CD.
24、(10分)动手画一画在同一平面内有12条直线,最少把平面分成几部分?最多分成几部分?
25、(9分)
已知:如图,BC⊥DC,BE平分∠ABC,AE平分∠BAD,∠1+∠2=90°,探究:DA与DC的位置关系.
26、(11分)如图(1),将两块直角三角尺的直角顶点C叠放在一起;
(1)若∠DCE=32°,∠ACB=______;若∠ACB=145°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE
的大小又有何关系,请说明理由.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
B
D
C
A
C
D
C
二、填空题(共10小题
每题3分
共30分)
11、55°
12、72或108
13、∠α+∠γ-∠β=180°
14、45°
15、70°或22°
16、90°
17、150°
18、①④⑤
19、4
20、1,5;3,6.
三、解答题(共6题
共60分)
21、(8分)
如图,AB∥CD,EF分别交AB、CD于点M、N,∠1=48°,MG平分∠BMF,MG
交CD于G,求∠2的度数.
解:∵∠1=48°(
已知
),
∴∠BMF=
132°
(
邻补角定义
).
∵MG平分∠BMF
,
∴∠BMG=
∠BMF
=
66°
(
角平分线定义
).
∵AB∥CD(
已知
),
∴∠2=
∠BMG
=
66°
(
两直线平行内错角
).
22、(12分)
如图,直线AB、CD、EF相交于点O.
(1)若∠1=21°,∠2=32°,求∠3的度数;
(2)
若9∠2=2∠3,∠1=26°,求∠AOF的度数;
(3)
若∠3-∠2=96°,∠1=20°,求∠EOB的度数;
解:(1)∵直线AB、CD、EF相交于点O.
∴∠1=∠DOF=21°,∠2=∠AOE=32°,
∵∠AOE+∠3+∠DOF=180°,
∴∠3=127°.
(2)设∠2=x°,则∠3=x°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+x+26=180.
解得x=28°,x°=126°.
∴∠2=28°,∠3=126°.
∴∠AOF=∠AOD+∠DOF=∠3+∠1=152°.
(3)设∠2=x°,则∠3=x°+96°,
∵∠AOE+∠3+∠DOF=180°,
∴∠2+∠3+∠1=180°,
即:x+
x+96+20=180.
解得x=32°,x°+96°=128°.
∴∠2=32°,∠3=128°.
∴∠EOB=∠1+∠COB=∠1+∠3=20°+128°=148°.
23、(10分)
如图,已知∠A+∠APC+∠C=360°,试说明:AB∥CD.
解:如答题图,过点P作PE∥AB,
∵PE∥AB,
∴∠A+∠1=180°.
∵∠APC=∠1+∠2,∠A+∠APC+∠C=360°,
∴∠A+∠1+∠2+∠C=360°.
∴∠2+∠C=180°.
∴PE∥CD.
∴AB∥CD.
24、(10分)动手画一画在同一平面内有12条直线,最少把平面分成几部分?最多分成几部分?
解:(1)有一条直线时,最少分成2部分,最多分成1+1=2部分;
(2)有两条直线时,最少分成4部分,最多分成1+1+2=4部分;
(3)有三条直线时,最少分成6部分,最多分成1+1+2+3=7部分;
(4)设直线条数有n条,分成的平面最多有a个,最少有b个,有以下规律:
m=1+1+2+3+…+(n-1)+n=,b=2n;
所以平面内有12条直线最多可将平面分成=79部分,最少2×12=24部分.
25、(9分)
已知:如图,BC⊥DC,BE平分∠ABC,AE平分∠BAD,∠1+∠2=90°,探究:DA与DC的位置关系.
解:∵AE平分∠BAD,BE平分∠ABC,
∴∠BAD=2∠1,∠ABC=2∠2
∴∠BAD+∠ABC=2∠1+2∠2=2(∠1+∠2),
∵∠1+∠2=90°,
∴∠BAD+∠ABC=2∠1+2∠2=2×90°=180°,
∴AD∥BC,
∴∠D+∠C=180°,
∵BC⊥DC,,
∴∠C=90°,
∴∠D=90°
∴DA⊥DC.
26、(11分)如图(1),将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=32°,∠ACB=______;若∠ACB=145°,则∠DCE=______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE
的大小又有何关系,请说明理由.
(1)∵∠ECB=90°,∠DCE=32°
∴∠DCB=90°-32°=58°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=148°,
∵∠ACB=145°,∠ACD=90°
∴∠DCB=145°-90°=55°
∵∠ECB=90°
∴∠DCE=90°-55°=35°,
故答案为:148°,35°
(2)猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°.
(3)∠DAB+∠CAE=120°
理由如下:由于∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°.
第23题图(1)
第18题图
第4题图
第11题图
第26题图(2)
第25题图
第23题图
第23题图
第22题图
第3题图
第6题图
第21题图
第25题图
第23题图
第26题图(2)
第22题图
第21题图
第13题图
第19题图
第23题图(1)
第17题图
第6题图
第6题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
