8.1.2.1 幂的乘方 课件(共22张PPT)
文档属性
| 名称 | 8.1.2.1 幂的乘方 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
2.幂的乘方与积的乘方
第1课时
幂的乘方
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解幂的乘方的运算性质.
2.运用幂的乘方的运算性质进行计算.
【过程与方法】
在探索幂的乘方运算性质的过程中,培养和发展学生学习数学的主动性,提高数学概括和表达能力.
【情感态度】
通过积极参与数学学习活动,培养学生积极探索,团结合作的学习习惯,激发学生学习数学的兴趣.
【教学重点】
理解并正确运用幂的乘方的运算性质.
【教学难点】
幂的乘方运算性质的灵活运用.
新课导入
地球、木星、太阳可以近似地看作球体.木星、太阳的半径分别约是地球半径的10倍和102倍,它们的体积分别约是地球的______倍和______倍.
103
106
体积扩大的倍数比半径扩大的倍数大得多.
思考:(102)3=106,为什么?
(102)3
=102×102×102
(根据___________).
幂的意义
=102+2+2
(根据___________________).
同底数幂的乘法性质
=106
=102×3
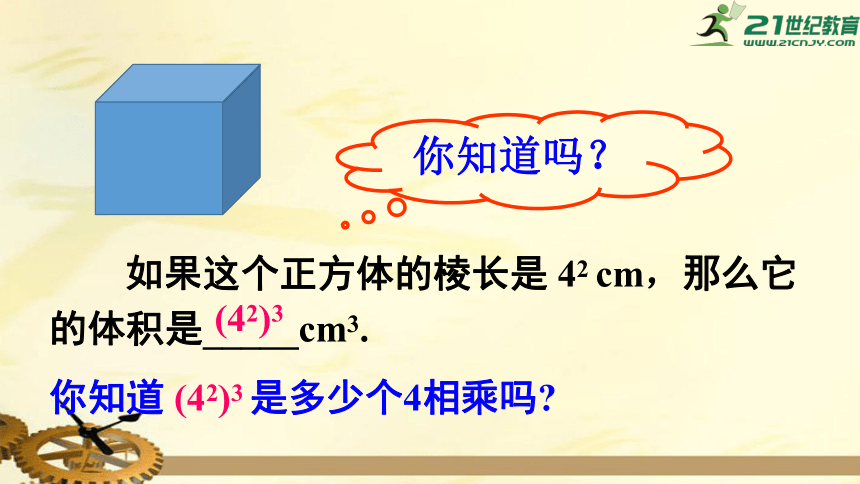
如果这个正方体的棱长是
42
cm,那么它的体积是_____cm3.
(42)3
你知道吗?
你知道
(42)3
是多少个4相乘吗?
想一想
幂的乘方,底数变不变?
指数应怎样计算?
其中
m
,
n
都是正整数.
进行新课
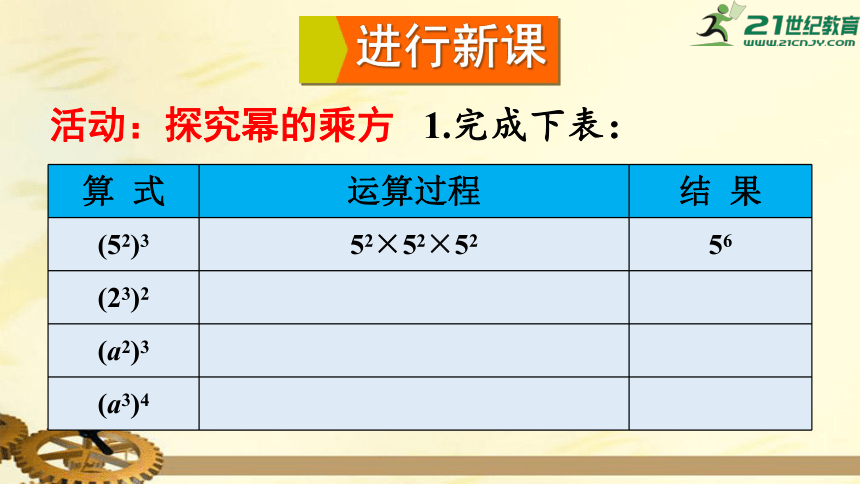
活动:探究幂的乘方
1.完成下表:
算
式
运算过程
结
果
(52)3
52×52×52
56
(23)2
23×23
26
(a2)3
a2×a2×a2
a6
(a3)4
a3×a3×a3×a3
a12
思考
请同学们观察下面各题左右两边,底数、指数有什么关系?
(52)3
=
5(
)
(23)2
=
2(
)
(a3)4
=
a(
)
6
=
5(
);
=
2(
);
=
a(
)
.
3×2
2×3
3×4
猜想:
(
am
)n=
?
(当m、n都是正整数)
6
12
(
am
)n
=
am·am·
…
·am
n个am
=
am+m+
…
+m
n个m
=
amn
归纳小结
幂的乘方性质:
其中
m
,
n
都是正整数.
幂的乘方:底数_____,指数_____.
不变
相乘
例2
计算:
(1)(105)3;(2)(x4)2;(3)(﹣a2)3.
练一练
计算:
⑴
(104)2
;
⑵
(am)4
(m为正整数);
⑶
-
(x3)2;
⑷
(-yn)5;
⑸
[(x-y)2]3;
⑹
[(a3)2]5.
⑹
[(a3)2]5
=
=104×2
=108
;
⑴(104)2
解:
⑵
(am)4
=
am×4
=
a4m
;
⑶
-(x3)2
=-x3×2
=-x6
;
⑷
(-yn)5
=-yn×5
=-y5n
;
⑸
[(x-y)2]3
=
(x-
y)2×3
=
(x-
y)6;
(a3×2)5
=a3×2×5
=a30.
=-(yn)5
推广:[(am)n]p=(amn)p=amnp
(m、n、p都是正整数).
随堂练习
1.
计算
(a2)3
的结果是(
)
A.
3a2
B.
2a3
C.
a5
D.
a6
2.
计算:(1)(103)4;(2)(-a5)6;(3)-(a5)3;
D
原式=1012
原式=
a30
原式=
-a15
3.
若2x+5y-3=0,求4x·32y的值.
解:4x·32y=22x·25y=22x+5y=23=8
4.
若10x=m,10y=n,则102x+3y的值为(
)
A.2m+3n
B.m2+n2
C.6mn
D.m2n3
D
5.
阅读下列解题过程:
试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,且16<27,所以2100<375.
试根据上述解答过程解决问题:比较2555,3444,4333的大小.
解:因为2555=(25)111=32111,3444=(34)111=81111,4333=(43)111=64111,且32<64<81,所以2111<4333<3444.
课堂小结
幂的乘方性质:
其中
m
,
n
都是正整数.
幂的乘方:底数_____,指数_____.
不变
相乘
课后作业
1.完成课本P48练习1-2;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
2.幂的乘方与积的乘方
第1课时
幂的乘方
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解幂的乘方的运算性质.
2.运用幂的乘方的运算性质进行计算.
【过程与方法】
在探索幂的乘方运算性质的过程中,培养和发展学生学习数学的主动性,提高数学概括和表达能力.
【情感态度】
通过积极参与数学学习活动,培养学生积极探索,团结合作的学习习惯,激发学生学习数学的兴趣.
【教学重点】
理解并正确运用幂的乘方的运算性质.
【教学难点】
幂的乘方运算性质的灵活运用.
新课导入
地球、木星、太阳可以近似地看作球体.木星、太阳的半径分别约是地球半径的10倍和102倍,它们的体积分别约是地球的______倍和______倍.
103
106
体积扩大的倍数比半径扩大的倍数大得多.
思考:(102)3=106,为什么?
(102)3
=102×102×102
(根据___________).
幂的意义
=102+2+2
(根据___________________).
同底数幂的乘法性质
=106
=102×3
如果这个正方体的棱长是
42
cm,那么它的体积是_____cm3.
(42)3
你知道吗?
你知道
(42)3
是多少个4相乘吗?
想一想
幂的乘方,底数变不变?
指数应怎样计算?
其中
m
,
n
都是正整数.
进行新课
活动:探究幂的乘方
1.完成下表:
算
式
运算过程
结
果
(52)3
52×52×52
56
(23)2
23×23
26
(a2)3
a2×a2×a2
a6
(a3)4
a3×a3×a3×a3
a12
思考
请同学们观察下面各题左右两边,底数、指数有什么关系?
(52)3
=
5(
)
(23)2
=
2(
)
(a3)4
=
a(
)
6
=
5(
);
=
2(
);
=
a(
)
.
3×2
2×3
3×4
猜想:
(
am
)n=
?
(当m、n都是正整数)
6
12
(
am
)n
=
am·am·
…
·am
n个am
=
am+m+
…
+m
n个m
=
amn
归纳小结
幂的乘方性质:
其中
m
,
n
都是正整数.
幂的乘方:底数_____,指数_____.
不变
相乘
例2
计算:
(1)(105)3;(2)(x4)2;(3)(﹣a2)3.
练一练
计算:
⑴
(104)2
;
⑵
(am)4
(m为正整数);
⑶
-
(x3)2;
⑷
(-yn)5;
⑸
[(x-y)2]3;
⑹
[(a3)2]5.
⑹
[(a3)2]5
=
=104×2
=108
;
⑴(104)2
解:
⑵
(am)4
=
am×4
=
a4m
;
⑶
-(x3)2
=-x3×2
=-x6
;
⑷
(-yn)5
=-yn×5
=-y5n
;
⑸
[(x-y)2]3
=
(x-
y)2×3
=
(x-
y)6;
(a3×2)5
=a3×2×5
=a30.
=-(yn)5
推广:[(am)n]p=(amn)p=amnp
(m、n、p都是正整数).
随堂练习
1.
计算
(a2)3
的结果是(
)
A.
3a2
B.
2a3
C.
a5
D.
a6
2.
计算:(1)(103)4;(2)(-a5)6;(3)-(a5)3;
D
原式=1012
原式=
a30
原式=
-a15
3.
若2x+5y-3=0,求4x·32y的值.
解:4x·32y=22x·25y=22x+5y=23=8
4.
若10x=m,10y=n,则102x+3y的值为(
)
A.2m+3n
B.m2+n2
C.6mn
D.m2n3
D
5.
阅读下列解题过程:
试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,且16<27,所以2100<375.
试根据上述解答过程解决问题:比较2555,3444,4333的大小.
解:因为2555=(25)111=32111,3444=(34)111=81111,4333=(43)111=64111,且32<64<81,所以2111<4333<3444.
课堂小结
幂的乘方性质:
其中
m
,
n
都是正整数.
幂的乘方:底数_____,指数_____.
不变
相乘
课后作业
1.完成课本P48练习1-2;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
