8.1.3同底数幂的除法(第1课时)同底数幂的除法 课件(共22张PPT)
文档属性
| 名称 | 8.1.3同底数幂的除法(第1课时)同底数幂的除法 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 23:08:39 | ||
图片预览





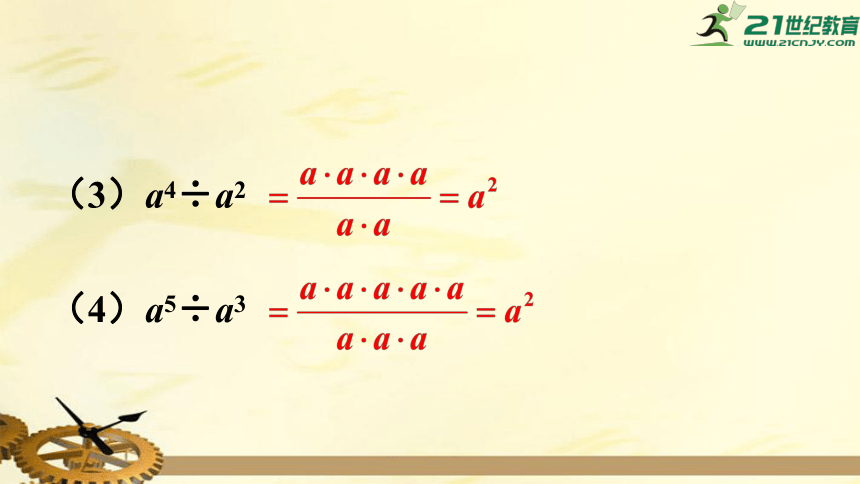

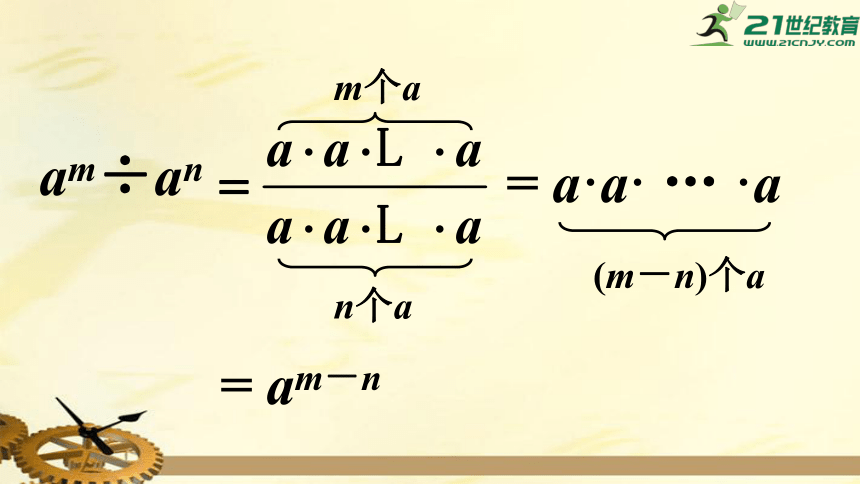

文档简介
(共22张PPT)
3.同底数幂的除法
第1课时
同底数幂的除法
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解同底数幂的除法的运算性质.
2.运用同底数幂的除法的运算性质进行计算.
【过程与方法】
通过探索同底数幂的除法运算性质的过程,体会由特殊到一般、类比等数学思想方法,提高观察、分析和概括的能力.
【情感态度】
通过参与数学学习活动,培养学生积极探索,合作交流的意识,提高学习数学的兴趣.
【教学重点】
理解并正确运用同底数幂的除法运算性质.
【教学难点】
同底数幂的除法运算性质的灵活运用.
复习导入
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
思考:
1.同底数幂相乘,底数不变,指数相加.
2.幂的乘方,底数不变,指数相乘.
3.积的乘方,等于每一个因式乘方的积
.
进行新课
活动:探究同底数幂的除法
1.用你熟悉的方法计算:
(1)35÷32
(2)46÷43
(3)a4÷a2
(4)a5÷a3
思考
请同学们观察下面各题左右两边,底数、指数有什么关系?
35÷32=
3(
)
46÷43=
4(
)
a5÷a3=
a(
)
3
=
3(
);
=
4(
);
=
a(
)
.
6-3
5-2
5-3
猜想:
am÷an=
?
(当m、n都是正整数)
3
2
am÷an
m个a
n个a
=
am-n
=
a·a·
…
·a
(m-n)个a
归纳小结
同底数幂相除:
其中
m
,
n
都是正整数,且m>n.
同底数幂相除,:底数_____,指数_____.
不变
相减
例
计算:
(1)
a7÷a4
;
(2)
(-x)6÷(-x)3;
(3)
(xy)4÷(xy)
;
(4)
b2m+2÷b2
.
=
a7–4
=
a3
;
(1)
a7÷a4
解:
(2)
(-x)6÷(-x)3
=
(-x)6–3
=
(-x)3
(3)
(xy)4÷(xy)
=(xy)4–1
(4)
b2m+2÷b2
=
b2m+2
–
2
=
-x3
;
=(xy)3
=x3y3
;
=
b2m
.
练一练
1.计算:
(1).(
)×27=215
(2).(
)×53=55
(3).(
)×105=107
(4).(
)×a4=a7
28
a3
52
102
根据乘法与除法互为逆运算得:
(1).
215÷27=
(2).
55÷53=
(3).
107÷105=
(4).
a7÷a4=
102
52
28
a3
2.下面的计算对不对?如果不对,应怎样改正?
(1)a10÷a2=a5;
(2)x5÷x4=x;
(3)a3÷a=a3;
(4)(-b)4÷(-b)2=-b2;
(5)(-x)6÷(-x)=x6;
(6)(-y)3÷y2=y.
同底数幂除法注意事项:
不要把
x
的指数误认为是0.
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1,如:
随堂练习
1.
计算
x6÷x2
正确的结果是(
).
A.
3
B.
x3
C.
x4
D.
x8
2.
计算:
x10÷x4÷x2
=
______.
3.
计算:(-ax)5÷(ax)3
=
______.
C
x4
-a2x2
4.
计算:
(1)y4÷y3;
(2)(-m)5÷(-m)2;
(3)(-m3)3÷m5;
(4)(x-y)10÷(y-x)5.
原式=y
原式=-m3
原式=-m4
原式=(y-x)5
5.
计算:
(1)(xy)5÷(xy)3÷(-xy);
(2)(x-y)10÷(y-x)4·(x-y)2.
原式=-xy
原式=(x-y)8
6.
若2x=3,2y=6,2z=12,求x,y,z之间的数量关系.
解:因为2y÷2x=2y-x=6÷3=2,2z÷2y=2z-y=2,所以2y-x=2z-y,即y-x=z-y,所以2y=x+z
.
课堂小结
同底数幂相除:
其中
m
,
n
都是正整数,且m>n.
同底数幂相除,:底数_____,指数_____.
不变
相减
课后作业
1.完成课本P50练习1;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
3.同底数幂的除法
第1课时
同底数幂的除法
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解同底数幂的除法的运算性质.
2.运用同底数幂的除法的运算性质进行计算.
【过程与方法】
通过探索同底数幂的除法运算性质的过程,体会由特殊到一般、类比等数学思想方法,提高观察、分析和概括的能力.
【情感态度】
通过参与数学学习活动,培养学生积极探索,合作交流的意识,提高学习数学的兴趣.
【教学重点】
理解并正确运用同底数幂的除法运算性质.
【教学难点】
同底数幂的除法运算性质的灵活运用.
复习导入
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
思考:
1.同底数幂相乘,底数不变,指数相加.
2.幂的乘方,底数不变,指数相乘.
3.积的乘方,等于每一个因式乘方的积
.
进行新课
活动:探究同底数幂的除法
1.用你熟悉的方法计算:
(1)35÷32
(2)46÷43
(3)a4÷a2
(4)a5÷a3
思考
请同学们观察下面各题左右两边,底数、指数有什么关系?
35÷32=
3(
)
46÷43=
4(
)
a5÷a3=
a(
)
3
=
3(
);
=
4(
);
=
a(
)
.
6-3
5-2
5-3
猜想:
am÷an=
?
(当m、n都是正整数)
3
2
am÷an
m个a
n个a
=
am-n
=
a·a·
…
·a
(m-n)个a
归纳小结
同底数幂相除:
其中
m
,
n
都是正整数,且m>n.
同底数幂相除,:底数_____,指数_____.
不变
相减
例
计算:
(1)
a7÷a4
;
(2)
(-x)6÷(-x)3;
(3)
(xy)4÷(xy)
;
(4)
b2m+2÷b2
.
=
a7–4
=
a3
;
(1)
a7÷a4
解:
(2)
(-x)6÷(-x)3
=
(-x)6–3
=
(-x)3
(3)
(xy)4÷(xy)
=(xy)4–1
(4)
b2m+2÷b2
=
b2m+2
–
2
=
-x3
;
=(xy)3
=x3y3
;
=
b2m
.
练一练
1.计算:
(1).(
)×27=215
(2).(
)×53=55
(3).(
)×105=107
(4).(
)×a4=a7
28
a3
52
102
根据乘法与除法互为逆运算得:
(1).
215÷27=
(2).
55÷53=
(3).
107÷105=
(4).
a7÷a4=
102
52
28
a3
2.下面的计算对不对?如果不对,应怎样改正?
(1)a10÷a2=a5;
(2)x5÷x4=x;
(3)a3÷a=a3;
(4)(-b)4÷(-b)2=-b2;
(5)(-x)6÷(-x)=x6;
(6)(-y)3÷y2=y.
同底数幂除法注意事项:
不要把
x
的指数误认为是0.
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1,如:
随堂练习
1.
计算
x6÷x2
正确的结果是(
).
A.
3
B.
x3
C.
x4
D.
x8
2.
计算:
x10÷x4÷x2
=
______.
3.
计算:(-ax)5÷(ax)3
=
______.
C
x4
-a2x2
4.
计算:
(1)y4÷y3;
(2)(-m)5÷(-m)2;
(3)(-m3)3÷m5;
(4)(x-y)10÷(y-x)5.
原式=y
原式=-m3
原式=-m4
原式=(y-x)5
5.
计算:
(1)(xy)5÷(xy)3÷(-xy);
(2)(x-y)10÷(y-x)4·(x-y)2.
原式=-xy
原式=(x-y)8
6.
若2x=3,2y=6,2z=12,求x,y,z之间的数量关系.
解:因为2y÷2x=2y-x=6÷3=2,2z÷2y=2z-y=2,所以2y-x=2z-y,即y-x=z-y,所以2y=x+z
.
课堂小结
同底数幂相除:
其中
m
,
n
都是正整数,且m>n.
同底数幂相除,:底数_____,指数_____.
不变
相减
课后作业
1.完成课本P50练习1;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
