17.2勾股定理逆定理(第1课时) 课件(共22张PPT)
文档属性
| 名称 | 17.2勾股定理逆定理(第1课时) 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 14:58:14 | ||
图片预览








文档简介
(共22张PPT)
第十七章
勾股定理
人教版
八年级下
17.2
勾股定理逆定理
第1课时
勾股定理逆定理
学习目标
1.理解勾股定理的逆定理.
2.了解逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题.
重点:勾股定理的逆定理.
难点:勾股定理的逆定理.
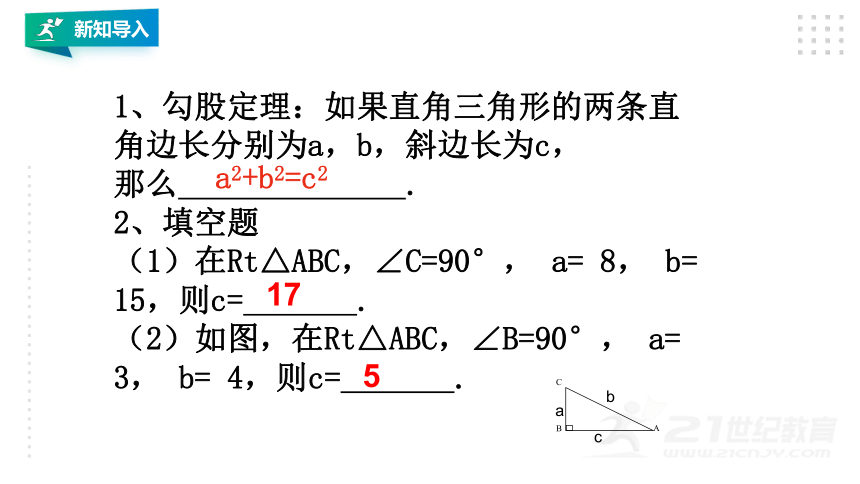
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么
.
2、填空题
(1)在Rt△ABC,∠C=90°,
a=
8,
b=
15,则c=
.
(2)如图,在Rt△ABC,∠B=90°,
a=
3,
b=
4,则c=
.
C
A
B
c
a
b
a2+b2=c2
17
5
新知导入
新知导入
同学们,你们知道古埃及人用什么方法得到直角吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
知识点一
勾股定理的逆定理
画△ABC,使①a=3cm,b=4cm,c=5cm;
②a=2.5cm,b=6cm,c=6.5cm;
③a=4cm,b=7.5cm,c=8.5cm.
以上a、b、c的关系都满足__________;
△ABC是________
三角形.
a2+b2=c2
直角
请完成下面练习并体验知识点的形成过程.
新知讲解
新知讲解
由上面几个例子,我们猜想:
命题2
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
练一练
如果三条线段长a、b、c满足
,这三条线段组成的三角形是不是直角三角形?为什么?
根据题意,因为三角形的三边长度a、b、c满足a2+b2=c2
,则根据命题2,这个三角形是直角三角形.
新知讲解
知识点二
证明勾股定理的逆定理
已知:△ABC的三边长分别为a、b、c,且a2+b2=c2.
求证:∠C=90°.
证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌
△A′B′C′(SSS),
∴∠C=
∠C′=90°
,
即△ABC是直角三角形.
则
A
C
a
B
b
c
归纳总结
勾股定理的逆定理:
如果三角形的三边长a
、b
、c满足
a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形
,最长边所对应的角为直角.
特别说明:
典例精讲
例1
判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
解:(1)因为152+82=
__________=
_____
172=_____
所以
+
=
,
根据________________,这三角形是直角三角形.注:像8,15,17这样能够成为_____________
________的三个__
____,称为勾股数
225+64
289
289
152
82
172
勾股定理的逆定理
直角三角形三
条边长
正整数
总结归纳
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
知识点三
互逆命题与互逆定理
新知讲解
命题1
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2
如果三角形的三边长a
、b
、c满足a2+b2=c2,那么这个三角形是直角三角形.
前面我们学习了两个命题,分别为:
命题1:
直角三角形
a2+b2=c2
命题2:
直角三角形
a2+b2=c2
题设
结论
它们是题设和结论正好相反的两个命题.
问题1
两个命题的条件和结论分别是什么?
问题2
两个命题的条件和结论有何联系?
新知讲解
总结归纳
如果两个命题的题设、结论正好相反,那么这两个命题称为互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
例2
判断下列命题的真假,写出逆命题,并判断逆命题的真假:(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
解:(1)原命题是真命题.逆命题为:如果两条直线只有一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,那么ab<0.逆命题是真命题.
典例精讲
总结归纳
课堂练习
1.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
2.已知下列命题:①若a>b,则a2>b2;②若a=1,则
=a;③两个全等三角形的面积相等.④若a>1,则(a-1)°=1.
其中原命题与逆命题均为真命题的个数是( )
A.0
B.1
C.2
D.3
B
A
3.在△ABC中,∠A,
∠B,
∠C的对边分别a,b,c.
①若∠C-
∠B=
∠A,则△ABC是直角三角形;
②若c2=b2-a2,则△ABC是直角三角形,且∠C=90°;
③若(c+a)(c-a)=b2,则△ABC是直角三角形;
④若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形.
以上命题中的假命题个数是(
)
A.1个
B.2个
C.3个
D.4个
A
4.下列几组数:①9,12,15;②8,15,17;③7,24,25;④n2-1,2n,n2+1(n是大于1的整数),
其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
5.下列各组数能构成勾股数的是
(填序号)
①6,8,10;②7,8,10;③
,
,1.
D
①
课堂总结
1、勾股定理的逆定理:如果三角形的三边长a、b、c,满足
,那么这个三角形是直角三角形.
2、勾股定理的逆定理是判定
的一个依据.
3、能够成为直角三角形三条边长的三个____________,称为勾股数.
a2+b2=c2
一个三角形是直角三角形
正整数
https://www.21cnjy.com/help/help_extract.php
第十七章
勾股定理
人教版
八年级下
17.2
勾股定理逆定理
第1课时
勾股定理逆定理
学习目标
1.理解勾股定理的逆定理.
2.了解逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题.
重点:勾股定理的逆定理.
难点:勾股定理的逆定理.
1、勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么
.
2、填空题
(1)在Rt△ABC,∠C=90°,
a=
8,
b=
15,则c=
.
(2)如图,在Rt△ABC,∠B=90°,
a=
3,
b=
4,则c=
.
C
A
B
c
a
b
a2+b2=c2
17
5
新知导入
新知导入
同学们,你们知道古埃及人用什么方法得到直角吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
知识点一
勾股定理的逆定理
画△ABC,使①a=3cm,b=4cm,c=5cm;
②a=2.5cm,b=6cm,c=6.5cm;
③a=4cm,b=7.5cm,c=8.5cm.
以上a、b、c的关系都满足__________;
△ABC是________
三角形.
a2+b2=c2
直角
请完成下面练习并体验知识点的形成过程.
新知讲解
新知讲解
由上面几个例子,我们猜想:
命题2
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
练一练
如果三条线段长a、b、c满足
,这三条线段组成的三角形是不是直角三角形?为什么?
根据题意,因为三角形的三边长度a、b、c满足a2+b2=c2
,则根据命题2,这个三角形是直角三角形.
新知讲解
知识点二
证明勾股定理的逆定理
已知:△ABC的三边长分别为a、b、c,且a2+b2=c2.
求证:∠C=90°.
证明:作Rt△A′B′C′,使∠C′=90°,A′C′=b,B′C′=a,
∴△ABC≌
△A′B′C′(SSS),
∴∠C=
∠C′=90°
,
即△ABC是直角三角形.
则
A
C
a
B
b
c
归纳总结
勾股定理的逆定理:
如果三角形的三边长a
、b
、c满足
a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形
,最长边所对应的角为直角.
特别说明:
典例精讲
例1
判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=15,b=8,c=17.
(2)a=13,b=14,c=15.
解:(1)因为152+82=
__________=
_____
172=_____
所以
+
=
,
根据________________,这三角形是直角三角形.注:像8,15,17这样能够成为_____________
________的三个__
____,称为勾股数
225+64
289
289
152
82
172
勾股定理的逆定理
直角三角形三
条边长
正整数
总结归纳
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
知识点三
互逆命题与互逆定理
新知讲解
命题1
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2
如果三角形的三边长a
、b
、c满足a2+b2=c2,那么这个三角形是直角三角形.
前面我们学习了两个命题,分别为:
命题1:
直角三角形
a2+b2=c2
命题2:
直角三角形
a2+b2=c2
题设
结论
它们是题设和结论正好相反的两个命题.
问题1
两个命题的条件和结论分别是什么?
问题2
两个命题的条件和结论有何联系?
新知讲解
总结归纳
如果两个命题的题设、结论正好相反,那么这两个命题称为互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
例2
判断下列命题的真假,写出逆命题,并判断逆命题的真假:(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
解:(1)原命题是真命题.逆命题为:如果两条直线只有一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,那么ab<0.逆命题是真命题.
典例精讲
总结归纳
课堂练习
1.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
2.已知下列命题:①若a>b,则a2>b2;②若a=1,则
=a;③两个全等三角形的面积相等.④若a>1,则(a-1)°=1.
其中原命题与逆命题均为真命题的个数是( )
A.0
B.1
C.2
D.3
B
A
3.在△ABC中,∠A,
∠B,
∠C的对边分别a,b,c.
①若∠C-
∠B=
∠A,则△ABC是直角三角形;
②若c2=b2-a2,则△ABC是直角三角形,且∠C=90°;
③若(c+a)(c-a)=b2,则△ABC是直角三角形;
④若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形.
以上命题中的假命题个数是(
)
A.1个
B.2个
C.3个
D.4个
A
4.下列几组数:①9,12,15;②8,15,17;③7,24,25;④n2-1,2n,n2+1(n是大于1的整数),
其中是勾股数的有( )
A.1组
B.2组
C.3组
D.4组
5.下列各组数能构成勾股数的是
(填序号)
①6,8,10;②7,8,10;③
,
,1.
D
①
课堂总结
1、勾股定理的逆定理:如果三角形的三边长a、b、c,满足
,那么这个三角形是直角三角形.
2、勾股定理的逆定理是判定
的一个依据.
3、能够成为直角三角形三条边长的三个____________,称为勾股数.
a2+b2=c2
一个三角形是直角三角形
正整数
https://www.21cnjy.com/help/help_extract.php
