2020-2021学年黑龙江省哈尔滨市香坊区风华中学九年级(下)开学数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市香坊区风华中学九年级(下)开学数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 998.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 07:40:58 | ||
图片预览



文档简介
2020-2021学年黑龙江省哈尔滨市香坊区风华中学九年级(下)开学数学试卷(五四学制)
一、填空题(共10小题).
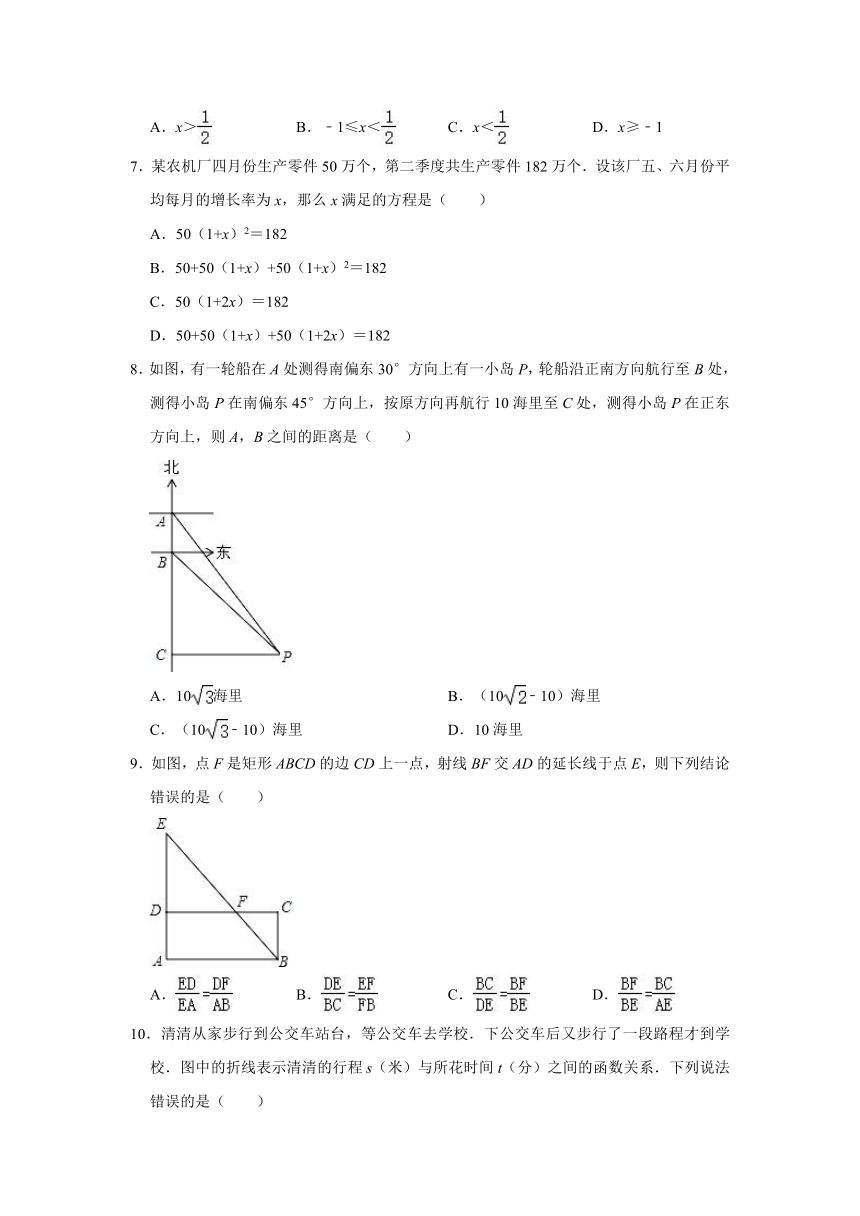
1.下列各数中,小于﹣2的数是( )
A.2 B.1 C.﹣1 D.﹣4
2.下列运算正确的是( )
A.a3?a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
3.下列图形中,既是中心对称,又是轴对称图形的是( )
A. B.
C. D.
4.在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
5.如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
A. B.
C. D.
6.不等式组的解集是( )
A.x> B.﹣1≤x< C.x< D.x≥﹣1
7.某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
8.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10﹣10)海里
C.(10﹣10)海里 D.10海里
9.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
10.清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
二、填空题(共10小题).
11.2012年广东省人口数超过104000000,将104000000这个数用科学记数法表示为 .
12.二次根式中,x的取值范围是 .
13.﹣= .
14.分解因式:4a2﹣16= .
15.如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为 .
16.一个扇形的面积为2πcm2,半径OA=3cm,则这个扇形的圆心角为 °.
17.二次函数y=﹣2(x﹣4)2+8的最大值为 .
18.已知矩形ABCD,E为CD的中点,F为AB上一点,连接EF,DF,若AB=4,BC=2,EF=,则DF的长为 .
19.袋中装有大小相同的2个红球和2个绿球.先从袋中摸出1个球后放回,混合均匀后再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是 .
20.已知:四边形ABCD,对角线AC,BD交于点E,AB⊥BD于B,∠BCD+2∠ABC=360°,BD=2,AC=,则tan∠AEB= .
三、解答题
21.先化简,再求值:÷(x+2﹣),其中x=2cos45°﹣tan60°.
22.如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以A为直角顶点的直角三角形ABE,点E在小正方形的顶点上,且△ABE的面积为5;
(2)在方格纸中画出以CD为一边的△CDF,点F在小正方形的顶点上,且△CDF的面积为3,CF与(1)中所画线段AE平行,连接BF,请直接写出线段BF的长.
23.某商店用1050元购进第一批某种文具盒,很快卖完.又用1440元购进第二批该种文具盒,但第二批每只文具盒的进价是第一批进价的1.2倍,数量比第一批多了10只.
(1)求第一批每只文具盒的进价是多少元?
(2)第二批文具盒按24元/只的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的文具盒全部按6折一次性打折销售,但要求第二批文具盒的利润率不低于20%,问至少销售多少只后开始打折?
24.如图,AB是⊙O的直径,C、D为⊙O上不同于A、B两点,并且C、D位于直径AB的两侧,CA=CD.
(1)如图1,求证:∠ABD=2∠BDC;
(2)如图2,AB、CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM;
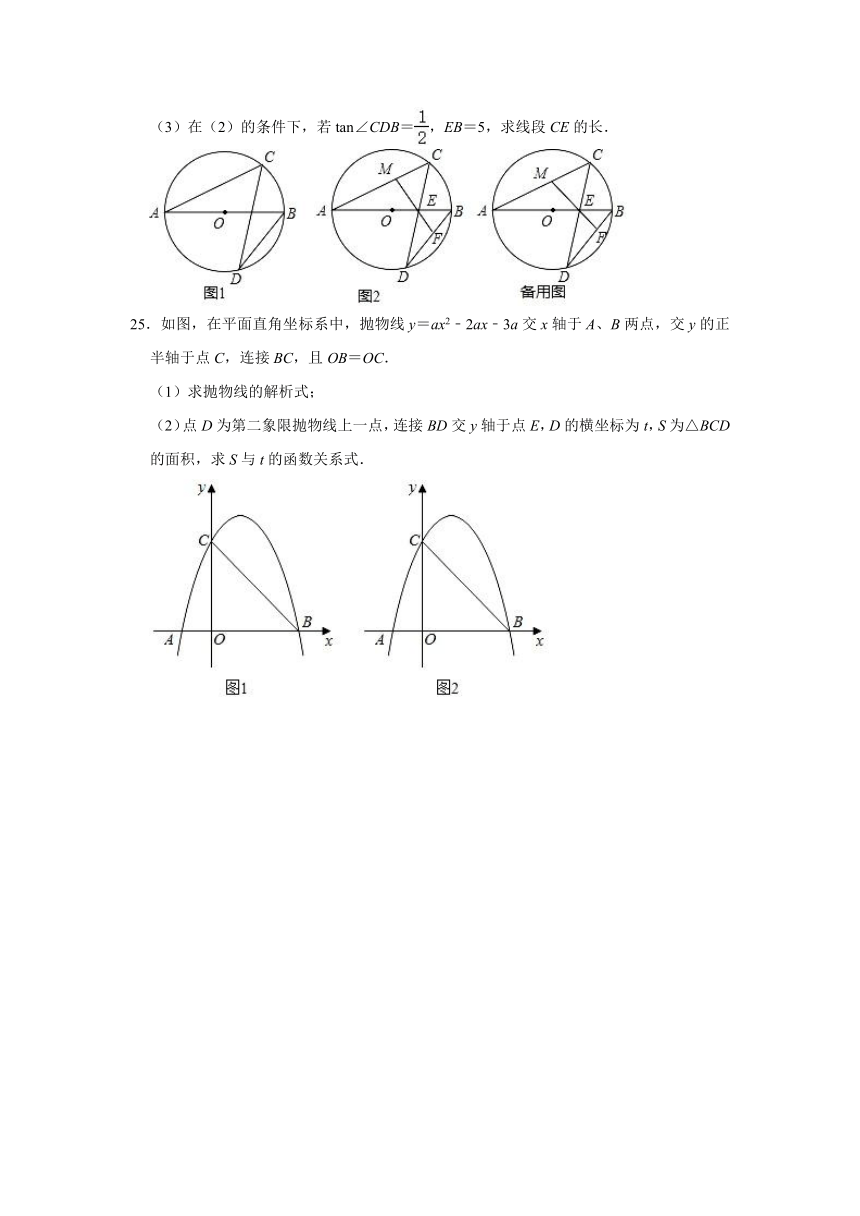
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点,交y的正半轴于点C,连接BC,且OB=OC.
(1)求抛物线的解析式;
(2)点D为第二象限抛物线上一点,连接BD交y轴于点E,D的横坐标为t,S为△BCD的面积,求S与t的函数关系式.
参考答案
一、填空题(共10小题).
1.下列各数中,小于﹣2的数是( )
A.2 B.1 C.﹣1 D.﹣4
解:比﹣2小的数是应该是负数,且绝对值大于2的数,
分析选项可得,只有D符合.
故选:D.
2.下列运算正确的是( )
A.a3?a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
解:A、原式=a5,不符合题意;
B、原式=x9,不符合题意;
C、原式=2x5,不符合题意;
D、原式=﹣a4,符合题意,
故选:D.
3.下列图形中,既是中心对称,又是轴对称图形的是( )
A. B.
C. D.
解:A、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误.
故选:A.
4.在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
解:反比例函数的图象上的每一条曲线上,y随x的增大而增大,
∴1﹣k<0,
∴k>1.
故选:D.
5.如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
A. B.
C. D.
解:从上边看第一列是两个小正方形,第二列是两个小正方形,第三列是一个小正方形,
故选:D.
6.不等式组的解集是( )
A.x> B.﹣1≤x< C.x< D.x≥﹣1
解:,由①得,x>,由②得,x≥﹣1,
故此不等式组的解集为:x>.
故选:A.
7.某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
解:依题意得五、六月份的产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
8.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10﹣10)海里
C.(10﹣10)海里 D.10海里
解:由题意得:∠CAP=30°,∠CBP=45°,BC=10海里,
在Rt△APC中,
∵∠CAP=30°,
∴AC===10(海里),
∴AB=AC﹣BC=(10﹣10)海里.
故选:C.
9.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
解:∵四边形ABCD为矩形,
∴AD∥BC,CD∥AB
∵DE∥BC,
∴=,=,所以B、选项结论正确,C选项错误;
∵DF∥AB,
∴=,所以A选项的结论正确;
=,
而BC=AD,
∴=,所以D选项的结论正确.
故选:C.
10.清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
解:A、依题意在第5min开始等公交车,第8min结束,故他等公交车时间为3min,故选项正确;
B、依题意得他离家400m共用了5min,故步行的速度为80米/分,故选项正确;
C、他公交车(20﹣8)min走了(6400﹣400)km,故公交车的速度为6000÷12=500m/min,故选项正确.
D、全程6800米,共用时25min,全程速度为272m/min,故选项错误;
故选:D.
二、填空题(共10小题).
11.2012年广东省人口数超过104000000,将104000000这个数用科学记数法表示为 1.04×108 .
解:将104000000这个数用科学记数法表示为1.04×108,
故答案为:1.04×108.
12.二次根式中,x的取值范围是 x≥2 .
解:根据题意,得
x﹣2≥0,
解得,x≥2;
故答案是:x≥2.
13.﹣= .
解:原式=3﹣2=,
故答案为:.
14.分解因式:4a2﹣16= 4(a+2)(a﹣2) .
解:4a2﹣16=4(a2﹣4)=4(a+2)(a﹣2).
故答案为:4(a+2)(a﹣2).
15.如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为 130° .
解:∵∠BCD=25°,
∴∠BOD=50°,
∴∠BCD=180°﹣50°=130°.
故答案为130°.
16.一个扇形的面积为2πcm2,半径OA=3cm,则这个扇形的圆心角为 80 °.
解:设扇形的圆心角为n°,
根据扇形的面积公式得,=2π,
∴n=80,
故答案为:80.
17.二次函数y=﹣2(x﹣4)2+8的最大值为 8 .
解:∵y=﹣2(x﹣4)2+8,
∴当x=4时,y取得最大值8,
故答案为:8.
18.已知矩形ABCD,E为CD的中点,F为AB上一点,连接EF,DF,若AB=4,BC=2,EF=,则DF的长为 或 .
解:分两种情况:
①点F靠近点A时,如图1所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
∴GE===1,
∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=2,
∵E是CD的中点,
∴DE=CD=2,
∴DG=2﹣1=1,
∴DF===;
②点F靠近点B时,如图2所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
同①得出EG=1,
∴DG=DE+EG=3,
∴DF===;
综上所述:DF的长为或.
19.袋中装有大小相同的2个红球和2个绿球.先从袋中摸出1个球后放回,混合均匀后再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是 .
解:画树状图得:
∵共有16种等可能的结果,两次摸到的球中有1个绿球和1个红球的有8种情况,
∴两次摸到的球中有1个绿球和1个红球的概率是:=.
故答案为:.
20.已知:四边形ABCD,对角线AC,BD交于点E,AB⊥BD于B,∠BCD+2∠ABC=360°,BD=2,AC=,则tan∠AEB= 3 .
解:作CH⊥BD于H,CF⊥AB于F,如图,
∵AB⊥BD,
∴CF∥BD,∠ABE=90°,
∴∠AEB=∠ACF,
∵∠BCD+2∠ABC=360°,
即∠BCD+2(∠1+90°)=360°,
∴∠BCD+2∠1=180°,
而∠BCD+∠1+∠2=180°,
∴∠1=∠2,
∴△BCD为等腰三角形,
∴BH=DH=BD=1,
易得四边形BFCH为矩形,
∴CF=BH=1,
在Rt△ACF中,AF==3,
∴tan∠ACF=3,
∴tan∠AEB=3.
故答案为3.
三、解答题
21.先化简,再求值:÷(x+2﹣),其中x=2cos45°﹣tan60°.
解:原式=÷
=?
=,
当x=2×﹣×=﹣3时,原式==.
22.如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以A为直角顶点的直角三角形ABE,点E在小正方形的顶点上,且△ABE的面积为5;
(2)在方格纸中画出以CD为一边的△CDF,点F在小正方形的顶点上,且△CDF的面积为3,CF与(1)中所画线段AE平行,连接BF,请直接写出线段BF的长.
解:(1)满足条件的点E如图所示.
(2)图中点F和点F′就是所求的点.
BF==或BF==5.
23.某商店用1050元购进第一批某种文具盒,很快卖完.又用1440元购进第二批该种文具盒,但第二批每只文具盒的进价是第一批进价的1.2倍,数量比第一批多了10只.
(1)求第一批每只文具盒的进价是多少元?
(2)第二批文具盒按24元/只的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的文具盒全部按6折一次性打折销售,但要求第二批文具盒的利润率不低于20%,问至少销售多少只后开始打折?
解:(1)设第一批每只文具盒的进价是x元,根据题意得:
﹣=10,
解得:x=15,
经检验,x=15是方程的解,
答:第一批文具盒的进价是15元/只;
(2)设销售y只后开始打折,根据题意得:
(24﹣15×1.2)y+(﹣y)(24×60%﹣15×1.2)≥1440×20%,
解得:y≥60,
答:至少销售60只后开始打折.
24.如图,AB是⊙O的直径,C、D为⊙O上不同于A、B两点,并且C、D位于直径AB的两侧,CA=CD.
(1)如图1,求证:∠ABD=2∠BDC;
(2)如图2,AB、CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM;
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
【解答】(1)证明:如图1中,连接OC、OD.
在△OCA和△OCD中,
,
∴△OCA≌△OCD,
∴∠ACO=∠DCO,
∵OA=OC,
∴∠A=∠ACO,
∵∠A=∠CDB,
∴∠CDB=∠OCD,
∴OC∥DB,
∠ABD=∠BOC,
∵∠BOC=2∠CDB,
∴∠ABD=2∠CDB.
(2)证明:如图2中,连接AD.
∵MF⊥BD,
∴∠EFB=90°,
∵AB是直径,
∴∠ADB=90°,
∴∠EFB=∠ADB,
∴EM∥AD,
∴∠CME=∠CAD,∠CEM=∠CDA,
∵CA=CD,
∴∠CAD=∠CDA,
∴∠CME=∠CEM,
∴CM=CE.
(3)解:如图3中,连接AD、BC,延长CO交AD于H.则CH⊥AD,AH=DH.
易知∠CDB=∠CAO=∠ACH,
∴tan∠CDB=tan∠CAO=tan∠ACH=,设AB=2a,
则BC=2a,AC=4a,AH=a,CH=a,
∴OH=CH﹣OC=a,
∴tan∠OAH===,
∵EF∥AD,
∴∠BEF=∠OAH,
∴tan∠BEF=,∵EB=5,
∴BF=3,EF=4,
∵tan∠EDF==,
∴DF=8,DE=4,BD=11,
∴AD=×11=,AB=×11=,
∴AE=AB﹣EB=,
∵∠ECB=∠EAD,∠EBC=∠EDA,
∴△ECB∽△EAD,
∴=,
∴=,
∴EC=.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点,交y的正半轴于点C,连接BC,且OB=OC.
(1)求抛物线的解析式;
(2)点D为第二象限抛物线上一点,连接BD交y轴于点E,D的横坐标为t,S为△BCD的面积,求S与t的函数关系式.
解:(1)令y=ax2﹣2ax﹣3a=0,
解得:x=﹣1或3,
故点A、B的坐标分别为(﹣1,0)、(3,0),
∵OB=OC,
即3=﹣3a,解得a=﹣1,
故抛物线的表达式为y=﹣x2+2x+3;
(2)由抛物线的表达式知,点C的坐标为(0,3),
∵D的横坐标为t,则点D的坐标为(t,﹣t2+2t+3),
设直线BD的表达式为y=kx+b,
将点B、D的坐标代入上式得:,解得,
故直线BD的表达式为y=(2﹣t)x+3t﹣6,
对于y=(2﹣t)x+3t﹣6,令x=0,则y=3t﹣6,故点E(0,3t﹣6),
则S=S△CED+S△CEB=CE×(xB﹣xD)=(3t﹣6)×(3﹣t)=﹣t2+t﹣9(﹣1<t<0),
即S=﹣t2+t﹣9(﹣1<t<0).
一、填空题(共10小题).
1.下列各数中,小于﹣2的数是( )
A.2 B.1 C.﹣1 D.﹣4
2.下列运算正确的是( )
A.a3?a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
3.下列图形中,既是中心对称,又是轴对称图形的是( )
A. B.
C. D.
4.在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
5.如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
A. B.
C. D.
6.不等式组的解集是( )
A.x> B.﹣1≤x< C.x< D.x≥﹣1
7.某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
8.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10﹣10)海里
C.(10﹣10)海里 D.10海里
9.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
10.清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
二、填空题(共10小题).
11.2012年广东省人口数超过104000000,将104000000这个数用科学记数法表示为 .
12.二次根式中,x的取值范围是 .
13.﹣= .
14.分解因式:4a2﹣16= .
15.如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为 .
16.一个扇形的面积为2πcm2,半径OA=3cm,则这个扇形的圆心角为 °.
17.二次函数y=﹣2(x﹣4)2+8的最大值为 .
18.已知矩形ABCD,E为CD的中点,F为AB上一点,连接EF,DF,若AB=4,BC=2,EF=,则DF的长为 .
19.袋中装有大小相同的2个红球和2个绿球.先从袋中摸出1个球后放回,混合均匀后再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是 .
20.已知:四边形ABCD,对角线AC,BD交于点E,AB⊥BD于B,∠BCD+2∠ABC=360°,BD=2,AC=,则tan∠AEB= .
三、解答题
21.先化简,再求值:÷(x+2﹣),其中x=2cos45°﹣tan60°.
22.如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以A为直角顶点的直角三角形ABE,点E在小正方形的顶点上,且△ABE的面积为5;
(2)在方格纸中画出以CD为一边的△CDF,点F在小正方形的顶点上,且△CDF的面积为3,CF与(1)中所画线段AE平行,连接BF,请直接写出线段BF的长.
23.某商店用1050元购进第一批某种文具盒,很快卖完.又用1440元购进第二批该种文具盒,但第二批每只文具盒的进价是第一批进价的1.2倍,数量比第一批多了10只.
(1)求第一批每只文具盒的进价是多少元?
(2)第二批文具盒按24元/只的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的文具盒全部按6折一次性打折销售,但要求第二批文具盒的利润率不低于20%,问至少销售多少只后开始打折?
24.如图,AB是⊙O的直径,C、D为⊙O上不同于A、B两点,并且C、D位于直径AB的两侧,CA=CD.
(1)如图1,求证:∠ABD=2∠BDC;
(2)如图2,AB、CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM;
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点,交y的正半轴于点C,连接BC,且OB=OC.
(1)求抛物线的解析式;
(2)点D为第二象限抛物线上一点,连接BD交y轴于点E,D的横坐标为t,S为△BCD的面积,求S与t的函数关系式.
参考答案
一、填空题(共10小题).
1.下列各数中,小于﹣2的数是( )
A.2 B.1 C.﹣1 D.﹣4
解:比﹣2小的数是应该是负数,且绝对值大于2的数,
分析选项可得,只有D符合.
故选:D.
2.下列运算正确的是( )
A.a3?a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
解:A、原式=a5,不符合题意;
B、原式=x9,不符合题意;
C、原式=2x5,不符合题意;
D、原式=﹣a4,符合题意,
故选:D.
3.下列图形中,既是中心对称,又是轴对称图形的是( )
A. B.
C. D.
解:A、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项错误.
故选:A.
4.在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
解:反比例函数的图象上的每一条曲线上,y随x的增大而增大,
∴1﹣k<0,
∴k>1.
故选:D.
5.如图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )
A. B.
C. D.
解:从上边看第一列是两个小正方形,第二列是两个小正方形,第三列是一个小正方形,
故选:D.
6.不等式组的解集是( )
A.x> B.﹣1≤x< C.x< D.x≥﹣1
解:,由①得,x>,由②得,x≥﹣1,
故此不等式组的解集为:x>.
故选:A.
7.某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
解:依题意得五、六月份的产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
8.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10﹣10)海里
C.(10﹣10)海里 D.10海里
解:由题意得:∠CAP=30°,∠CBP=45°,BC=10海里,
在Rt△APC中,
∵∠CAP=30°,
∴AC===10(海里),
∴AB=AC﹣BC=(10﹣10)海里.
故选:C.
9.如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
解:∵四边形ABCD为矩形,
∴AD∥BC,CD∥AB
∵DE∥BC,
∴=,=,所以B、选项结论正确,C选项错误;
∵DF∥AB,
∴=,所以A选项的结论正确;
=,
而BC=AD,
∴=,所以D选项的结论正确.
故选:C.
10.清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
解:A、依题意在第5min开始等公交车,第8min结束,故他等公交车时间为3min,故选项正确;
B、依题意得他离家400m共用了5min,故步行的速度为80米/分,故选项正确;
C、他公交车(20﹣8)min走了(6400﹣400)km,故公交车的速度为6000÷12=500m/min,故选项正确.
D、全程6800米,共用时25min,全程速度为272m/min,故选项错误;
故选:D.
二、填空题(共10小题).
11.2012年广东省人口数超过104000000,将104000000这个数用科学记数法表示为 1.04×108 .
解:将104000000这个数用科学记数法表示为1.04×108,
故答案为:1.04×108.
12.二次根式中,x的取值范围是 x≥2 .
解:根据题意,得
x﹣2≥0,
解得,x≥2;
故答案是:x≥2.
13.﹣= .
解:原式=3﹣2=,
故答案为:.
14.分解因式:4a2﹣16= 4(a+2)(a﹣2) .
解:4a2﹣16=4(a2﹣4)=4(a+2)(a﹣2).
故答案为:4(a+2)(a﹣2).
15.如图,AB是⊙O的直径,C,D两点在⊙O上,∠BCD=25°,则∠AOD的度数为 130° .
解:∵∠BCD=25°,
∴∠BOD=50°,
∴∠BCD=180°﹣50°=130°.
故答案为130°.
16.一个扇形的面积为2πcm2,半径OA=3cm,则这个扇形的圆心角为 80 °.
解:设扇形的圆心角为n°,
根据扇形的面积公式得,=2π,
∴n=80,
故答案为:80.
17.二次函数y=﹣2(x﹣4)2+8的最大值为 8 .
解:∵y=﹣2(x﹣4)2+8,
∴当x=4时,y取得最大值8,
故答案为:8.
18.已知矩形ABCD,E为CD的中点,F为AB上一点,连接EF,DF,若AB=4,BC=2,EF=,则DF的长为 或 .
解:分两种情况:
①点F靠近点A时,如图1所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
∴GE===1,
∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=2,
∵E是CD的中点,
∴DE=CD=2,
∴DG=2﹣1=1,
∴DF===;
②点F靠近点B时,如图2所示:
作FG⊥CD于G,
则FG=BC=2,∠FGE=90°,
同①得出EG=1,
∴DG=DE+EG=3,
∴DF===;
综上所述:DF的长为或.
19.袋中装有大小相同的2个红球和2个绿球.先从袋中摸出1个球后放回,混合均匀后再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是 .
解:画树状图得:
∵共有16种等可能的结果,两次摸到的球中有1个绿球和1个红球的有8种情况,
∴两次摸到的球中有1个绿球和1个红球的概率是:=.
故答案为:.
20.已知:四边形ABCD,对角线AC,BD交于点E,AB⊥BD于B,∠BCD+2∠ABC=360°,BD=2,AC=,则tan∠AEB= 3 .
解:作CH⊥BD于H,CF⊥AB于F,如图,
∵AB⊥BD,
∴CF∥BD,∠ABE=90°,
∴∠AEB=∠ACF,
∵∠BCD+2∠ABC=360°,
即∠BCD+2(∠1+90°)=360°,
∴∠BCD+2∠1=180°,
而∠BCD+∠1+∠2=180°,
∴∠1=∠2,
∴△BCD为等腰三角形,
∴BH=DH=BD=1,
易得四边形BFCH为矩形,
∴CF=BH=1,
在Rt△ACF中,AF==3,
∴tan∠ACF=3,
∴tan∠AEB=3.
故答案为3.
三、解答题
21.先化简,再求值:÷(x+2﹣),其中x=2cos45°﹣tan60°.
解:原式=÷
=?
=,
当x=2×﹣×=﹣3时,原式==.
22.如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以A为直角顶点的直角三角形ABE,点E在小正方形的顶点上,且△ABE的面积为5;
(2)在方格纸中画出以CD为一边的△CDF,点F在小正方形的顶点上,且△CDF的面积为3,CF与(1)中所画线段AE平行,连接BF,请直接写出线段BF的长.
解:(1)满足条件的点E如图所示.
(2)图中点F和点F′就是所求的点.
BF==或BF==5.
23.某商店用1050元购进第一批某种文具盒,很快卖完.又用1440元购进第二批该种文具盒,但第二批每只文具盒的进价是第一批进价的1.2倍,数量比第一批多了10只.
(1)求第一批每只文具盒的进价是多少元?
(2)第二批文具盒按24元/只的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的文具盒全部按6折一次性打折销售,但要求第二批文具盒的利润率不低于20%,问至少销售多少只后开始打折?
解:(1)设第一批每只文具盒的进价是x元,根据题意得:
﹣=10,
解得:x=15,
经检验,x=15是方程的解,
答:第一批文具盒的进价是15元/只;
(2)设销售y只后开始打折,根据题意得:
(24﹣15×1.2)y+(﹣y)(24×60%﹣15×1.2)≥1440×20%,
解得:y≥60,
答:至少销售60只后开始打折.
24.如图,AB是⊙O的直径,C、D为⊙O上不同于A、B两点,并且C、D位于直径AB的两侧,CA=CD.
(1)如图1,求证:∠ABD=2∠BDC;
(2)如图2,AB、CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM;
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
【解答】(1)证明:如图1中,连接OC、OD.
在△OCA和△OCD中,
,
∴△OCA≌△OCD,
∴∠ACO=∠DCO,
∵OA=OC,
∴∠A=∠ACO,
∵∠A=∠CDB,
∴∠CDB=∠OCD,
∴OC∥DB,
∠ABD=∠BOC,
∵∠BOC=2∠CDB,
∴∠ABD=2∠CDB.
(2)证明:如图2中,连接AD.
∵MF⊥BD,
∴∠EFB=90°,
∵AB是直径,
∴∠ADB=90°,
∴∠EFB=∠ADB,
∴EM∥AD,
∴∠CME=∠CAD,∠CEM=∠CDA,
∵CA=CD,
∴∠CAD=∠CDA,
∴∠CME=∠CEM,
∴CM=CE.
(3)解:如图3中,连接AD、BC,延长CO交AD于H.则CH⊥AD,AH=DH.
易知∠CDB=∠CAO=∠ACH,
∴tan∠CDB=tan∠CAO=tan∠ACH=,设AB=2a,
则BC=2a,AC=4a,AH=a,CH=a,
∴OH=CH﹣OC=a,
∴tan∠OAH===,
∵EF∥AD,
∴∠BEF=∠OAH,
∴tan∠BEF=,∵EB=5,
∴BF=3,EF=4,
∵tan∠EDF==,
∴DF=8,DE=4,BD=11,
∴AD=×11=,AB=×11=,
∴AE=AB﹣EB=,
∵∠ECB=∠EAD,∠EBC=∠EDA,
∴△ECB∽△EAD,
∴=,
∴=,
∴EC=.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点,交y的正半轴于点C,连接BC,且OB=OC.
(1)求抛物线的解析式;
(2)点D为第二象限抛物线上一点,连接BD交y轴于点E,D的横坐标为t,S为△BCD的面积,求S与t的函数关系式.
解:(1)令y=ax2﹣2ax﹣3a=0,
解得:x=﹣1或3,
故点A、B的坐标分别为(﹣1,0)、(3,0),
∵OB=OC,
即3=﹣3a,解得a=﹣1,
故抛物线的表达式为y=﹣x2+2x+3;
(2)由抛物线的表达式知,点C的坐标为(0,3),
∵D的横坐标为t,则点D的坐标为(t,﹣t2+2t+3),
设直线BD的表达式为y=kx+b,
将点B、D的坐标代入上式得:,解得,
故直线BD的表达式为y=(2﹣t)x+3t﹣6,
对于y=(2﹣t)x+3t﹣6,令x=0,则y=3t﹣6,故点E(0,3t﹣6),
则S=S△CED+S△CEB=CE×(xB﹣xD)=(3t﹣6)×(3﹣t)=﹣t2+t﹣9(﹣1<t<0),
即S=﹣t2+t﹣9(﹣1<t<0).
同课章节目录
