8.2.3 多项式与多项式相乘 课件(共23张PPT)
文档属性
| 名称 | 8.2.3 多项式与多项式相乘 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:52:04 | ||
图片预览







文档简介
(共23张PPT)
3.多项式与多项式相乘
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解多项式与多项式的乘法法则.
2.能运用多项式与多项式的乘法法则进行计算.
【过程与方法】
从实际问题引出多项式乘以多项式,通过探索多项式乘以多项式的计算法则,进一步体会转化思想和数形结合思想.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生观察、归纳的能力,通过合作交流,体验成功的喜悦.
【教学重点】
多项式与多项式相乘的计算法则.
【教学难点】
熟练地运用多项式与多项式相乘的计算法则进行计算.
复习导入
如何进行单项式乘单项式的运算?
单×单
=(系数×系数)(同底数幂×同底数幂)(单独的幂)
(2a2b3c)(-3ab)
=
-6a3b4c
如何进行单项式乘多项式的运算?
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
x(x-1)+2x(x+1)-3x(2x-5)
进行新课
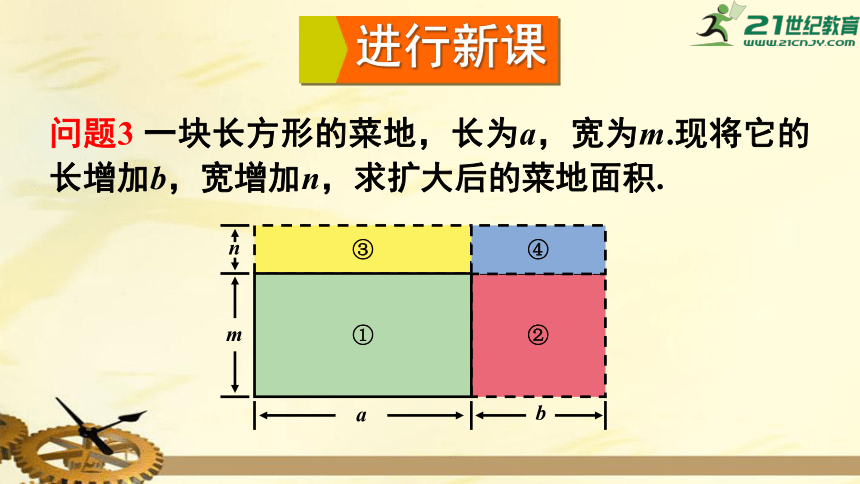
问题3
一块长方形的菜地,长为a,宽为m.现将它的长增加b,宽增加n,求扩大后的菜地面积.
②
③
①
④
a
b
m
n
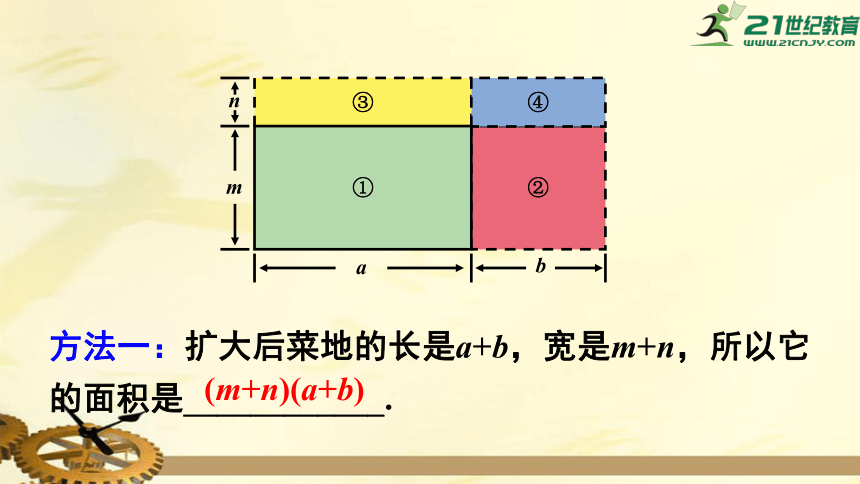
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是____________.
②
③
①
④
a
b
m
n
(m+n)(a+b)
方法二:先算4块小长方形的面积,再求总面积,扩大后菜地的面积是________________.
②
③
①
④
a
b
m
n
(ma+mb+na+nb)
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(a+b)(m+n)=
am
+
bm
+
an
+
bn
思考:你能运用所学的知识说明此等式成立的道理吗?
(a+b)(m+n)=
am
+
bm
+
an
+
bn
实际上,把(a+b)看成一个整体,有:
(a+b)(m+n)=
(a+b)m+(a+b)n
=
am+bm+an+bn
你能用语言表达这种运算的规律吗
?
1
2
3
4
(m+n)(a+b)
=
am
1
2
3
4
+bm
+an
+bn
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
例6
计算:
(1)(-2x-1)(3x-2);
(2)(ax+b)(cx+d).
解:(1)
(-2x-1)(3x-2)
=
(-2x)·3x+(-2x)·(-2)+(-1)·3x+(-1)×(-2)
=
-6x2+4x-3x+2
=
-6x2+x+2
(2)
(ax+b)(cx+d)
=
ax·cx+ax·d+b·cx+bd
=
acx2+(ad+bc)x+bd
例7
计算:
(1)(a+b)(a2-ab+b2);
(2)(y2+y+1)(y+2).
解:(1)
(a+b)(a2-ab+b2)
=
a·a2-a·ab+a·b2+b·a2-b·ab+b·b2
=
a3+b3
(2)
(y2+y+1)(y+2)
=
y3+2y2+y2+2y+y+2
=
y3+3y2+3y+2
练一练
计算:
(1)
(2)
(3)
(x-3y)(x-2y);
(x+5)(x-7);
(2m+3n)(2m-3n).
1.(x+5)(x+6);
2.(3x+4)(3x-4);
3.(xn-1)(xn+2);
4.(3x-1)(2x+3)-(x+3)(x-4).
快乐检测:
随堂练习
1.
计算(x+1)(x+2)的结果为(
)
A.
x2+2
B.
x2+3x+2
C.
x2+3x+3
D.
x2+2x+2
2.
计算
的结果为___________.
B
x3-2x2-2x+4
3.
计算:
(1)(4y-1)(y+5);
(2)(x+2y)(3x-4y);
原式=4y2+19y-5
原式=3x2+2xy-8y2
(3)(x+2)(x2-2x+4);
(4)(x-y)2-(x-2y)(x+y).
原式=x3+8
原式=3y2-xy
4.
若(x+2)(x2+mx+4)的展开式中不含有x的二次项,则m的值为______.
5.
当x=7时,求代数式(2x+5)(x+1)-(x-3)(x+1)的值.
-2
解:化简原式,得x2+9x+8,
当x=7时,原式
=
(7)2+9(7
)+8
=
120
.
课堂小结
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
多项式乘法法则
注意:
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类项之前),检验项数常常作为检验解题过程是否正确的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并.
课后作业
1.完成课本P64练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
3.多项式与多项式相乘
沪科版·七年级下册
上课课件
第8章
整式乘法与因式分解
学习目标
【知识与技能】
1.理解多项式与多项式的乘法法则.
2.能运用多项式与多项式的乘法法则进行计算.
【过程与方法】
从实际问题引出多项式乘以多项式,通过探索多项式乘以多项式的计算法则,进一步体会转化思想和数形结合思想.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生观察、归纳的能力,通过合作交流,体验成功的喜悦.
【教学重点】
多项式与多项式相乘的计算法则.
【教学难点】
熟练地运用多项式与多项式相乘的计算法则进行计算.
复习导入
如何进行单项式乘单项式的运算?
单×单
=(系数×系数)(同底数幂×同底数幂)(单独的幂)
(2a2b3c)(-3ab)
=
-6a3b4c
如何进行单项式乘多项式的运算?
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
x(x-1)+2x(x+1)-3x(2x-5)
进行新课
问题3
一块长方形的菜地,长为a,宽为m.现将它的长增加b,宽增加n,求扩大后的菜地面积.
②
③
①
④
a
b
m
n
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是____________.
②
③
①
④
a
b
m
n
(m+n)(a+b)
方法二:先算4块小长方形的面积,再求总面积,扩大后菜地的面积是________________.
②
③
①
④
a
b
m
n
(ma+mb+na+nb)
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(a+b)(m+n)=
am
+
bm
+
an
+
bn
思考:你能运用所学的知识说明此等式成立的道理吗?
(a+b)(m+n)=
am
+
bm
+
an
+
bn
实际上,把(a+b)看成一个整体,有:
(a+b)(m+n)=
(a+b)m+(a+b)n
=
am+bm+an+bn
你能用语言表达这种运算的规律吗
?
1
2
3
4
(m+n)(a+b)
=
am
1
2
3
4
+bm
+an
+bn
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
例6
计算:
(1)(-2x-1)(3x-2);
(2)(ax+b)(cx+d).
解:(1)
(-2x-1)(3x-2)
=
(-2x)·3x+(-2x)·(-2)+(-1)·3x+(-1)×(-2)
=
-6x2+4x-3x+2
=
-6x2+x+2
(2)
(ax+b)(cx+d)
=
ax·cx+ax·d+b·cx+bd
=
acx2+(ad+bc)x+bd
例7
计算:
(1)(a+b)(a2-ab+b2);
(2)(y2+y+1)(y+2).
解:(1)
(a+b)(a2-ab+b2)
=
a·a2-a·ab+a·b2+b·a2-b·ab+b·b2
=
a3+b3
(2)
(y2+y+1)(y+2)
=
y3+2y2+y2+2y+y+2
=
y3+3y2+3y+2
练一练
计算:
(1)
(2)
(3)
(x-3y)(x-2y);
(x+5)(x-7);
(2m+3n)(2m-3n).
1.(x+5)(x+6);
2.(3x+4)(3x-4);
3.(xn-1)(xn+2);
4.(3x-1)(2x+3)-(x+3)(x-4).
快乐检测:
随堂练习
1.
计算(x+1)(x+2)的结果为(
)
A.
x2+2
B.
x2+3x+2
C.
x2+3x+3
D.
x2+2x+2
2.
计算
的结果为___________.
B
x3-2x2-2x+4
3.
计算:
(1)(4y-1)(y+5);
(2)(x+2y)(3x-4y);
原式=4y2+19y-5
原式=3x2+2xy-8y2
(3)(x+2)(x2-2x+4);
(4)(x-y)2-(x-2y)(x+y).
原式=x3+8
原式=3y2-xy
4.
若(x+2)(x2+mx+4)的展开式中不含有x的二次项,则m的值为______.
5.
当x=7时,求代数式(2x+5)(x+1)-(x-3)(x+1)的值.
-2
解:化简原式,得x2+9x+8,
当x=7时,原式
=
(7)2+9(7
)+8
=
120
.
课堂小结
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
多项式乘法法则
注意:
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类项之前),检验项数常常作为检验解题过程是否正确的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并.
课后作业
1.完成课本P64练习1-3;
2.完成练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
