浙江省绍兴市柯桥区2020-2021学年第二学期七年级开学考试数学试题(word版 含答案)
文档属性
| 名称 | 浙江省绍兴市柯桥区2020-2021学年第二学期七年级开学考试数学试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 10:26:02 | ||
图片预览


文档简介
1149350010553700七年数学试题卷
一.选择题(每题2分,共20分)
1.﹣2020的相反数为( )
A.﹣ B.2020 C.﹣2020 D.
2.在π,,0,0.3,﹣,,3.121121112…(每两个2之间依次多一个1)中,无理数的个数有( )
A.5个 B.4个 C.3个 D.2个
3.2020年11月1日第七次全国人口普查在全国范围内展开.国家统计局表示,截止2019年底,中国大陆总人口为14.05亿,将14.05亿用科学记数法表示为( )
A.false B.false C.false D.false
4.如图,∠1和∠2不是同旁内角的是( )
A. B. C. D.
5.已知关于x的方程2x+8=﹣6与方程2x﹣3a=﹣5的解相同,则a的值为( )
A.13 B.3 C.﹣3 D.8
6.下列等式的变形中,正确的是( )
A.如果false,那么a=b B.如果∣a∣=∣b∣,那么a=b
C.如果ax =ay,那么x= y D.如果a=b,那么false
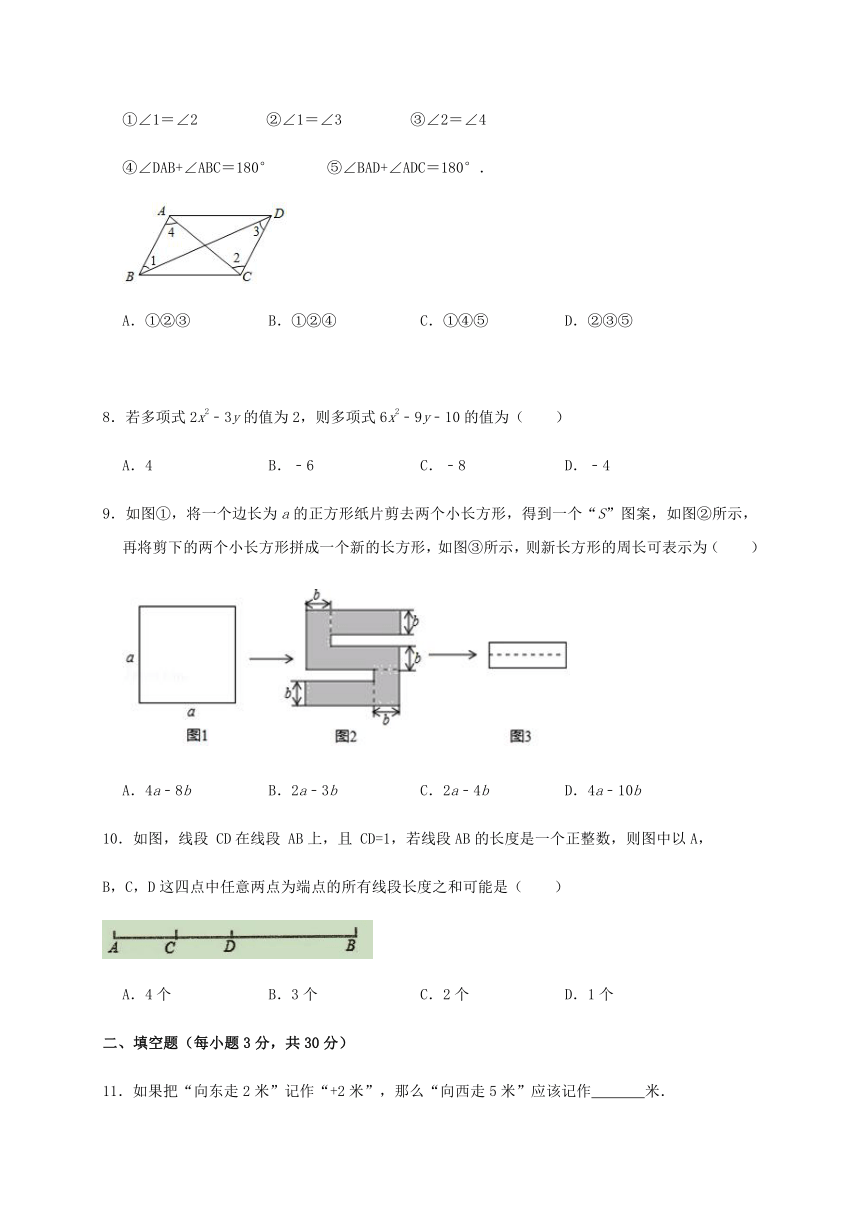
7.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2 ②∠1=∠3 ③∠2=∠4
④∠DAB+∠ABC=180° ⑤∠BAD+∠ADC=180°.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
8.若多项式2x2﹣3y的值为2,则多项式6x2﹣9y﹣10的值为( )
A.4 B.﹣6 C.﹣8 D.﹣4
9.如图①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图②所示,再将剪下的两个小长方形拼成一个新的长方形,如图③所示,则新长方形的周长可表示为( )
A.4a﹣8b B.2a﹣3b C.2a﹣4b D.4a﹣10b
10.如图,线段 CD在线段 AB上,且 CD=1,若线段AB的长度是一个正整数,则图中以A,
B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共30分)
11.如果把“向东走2米”记作“+2米”,那么“向西走5米”应该记作 米.
12.单项式﹣的系数是 ,次数是 .
13.0.47249≈ (精确到千分位).
一种商品每件成本是a元,原来按成本增加20%定出价格进销售,一段时间后,由于库存积压减价,按原价的9折出售,则现在每件售价为 元.
若实数a,b满足|a﹣2|+(b+3)2=0,则ba= .
16.若方程的解为则方程组的解为 .
17.已知A 、O、B 三点共线,∠BOC=35°,作 OD⊥OC,则∠DOB=___▲____
18.如图,已知∠1=(3x+24)°,∠2=(5x+20)°,要使m∥n,那么∠1= .
19.已知整数a1,a2,a3,a4,…满足下列条件∶a1=0,a2=-∣a1+1∣,a3=-∣a2+2∣,
a4=-∣a3+3∣,a5 =-∣a4+4∣,…,依此类推,则a2020的值为____
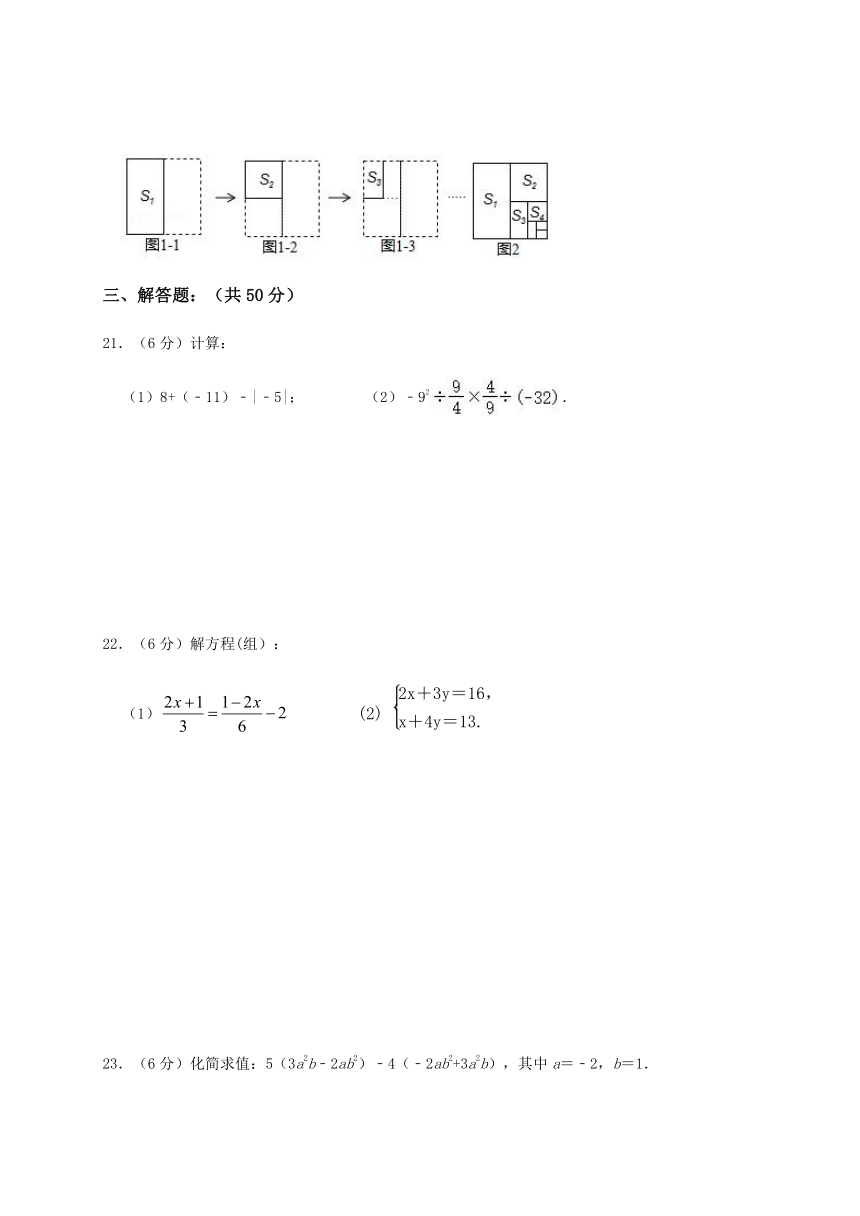
将边长为1的正方形纸片按图1所示方法进行对折,第1次对折后得到的图形面积为s1,第2次对折后得到的图形面积为s2,…,第n次对折后得到的图形面积为sn,请根据图2化简:s1+s2+s3+…+s2020= .
三、解答题:(共50分)
21.(6分)计算:
(1)8+(﹣11)﹣|﹣5|; (2)﹣92.
22.(6分)解方程(组):
(1)false (2)
(6分)化简求值:5(3a2b﹣2ab2)﹣4(﹣2ab2+3a2b),其中a=﹣2,b=1.
24.(6分)如图所示,已知点A,B,C,D,请按要求画出图形
(1)画直线AB和射线CB;
(2)连结AC,并在直线AB上用直尺和圆规作线段AE,使AE=2AC(要求保留作图痕迹);
(3)在直线AB上确定一点P,使PC+PD的和最短,并写出画图的依据。
25.(6分)给出定义如下:
若有理数a,b满足等式a+b=ab﹣1,则我们称a,b为一对“伴生有理数”,记为(a,b).例如:2+3=2×3﹣1,则称2,3是一对“伴生有理数”,记为(2,3).
(1)判断(,﹣3)、(7,)是否为“伴生有理数”,请说明理由;
(2)若(4,m)为“伴生有理数”,求m的值.
26.(6分)解关于x,y的方程组 false 时,甲正确地解出 false ,乙因为把c抄错了,误解为 false ,求2a+b—c的平方根.
27.(6分)如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
28.(8分)如图,城乡公交车行驶在笔直的公路上,这条路上有A,B,C三个站点,已知相邻两站之间的距离分别为false千米,false千米,且每个站点的停靠时间为4分钟.已知甲、乙两车于上午8:00分别从A站,C站出发相向而行,两车的速度均为30千米/小时,设两车出发t小时后,问:
(1)甲、乙两车到达B站分别用时多少?
(2)求两车相遇的时刻.
(3)当两车相距4千米时,求t的值.
七年级数学试卷参考答案
选择题:本题有10小题,每小题2分,共20分.
BCCDC ADDAB
二、填空题:本题有10小题,每小题3分,共30分.
11.-5 12.,3 13.0.472 14.1.08a 15.9
396938512065016 .false 17.1250或550 18.750 19.-1010 20. 2020
三、解答题:本题有8小题,共50分.
21.(6分)(1)-8 (2)false
22.(6分)(1)false (2)falsefalse
23.(6分)3a2b-2ab2 ; 16
24.(6分)画图略 理由:两点之间,线段最短
25(6分).解:(1)∵﹣3=﹣,×(﹣3)﹣1=﹣,
∴﹣3=×(﹣3)﹣1,
∴(,﹣3)是“伴生有理数”,
∵7+=,7×﹣1=,
∴7+≠7×﹣1,
∴(7,)不是“伴生有理数”;
(2)由题意得:4+m=4m﹣1,
解得m=.
故m的值.
26.(6分) 把 x=2,y=4 代入方程 3x?cy=?2 ,得:
6?4c=?2 ,
解得: c=2 .
把 {x=2y=4,{x=4y=?1 分别代入方程 ax+by=9 ,得:
{2a+4b=94a?b=9 ,
解得 :{a=52b=1 .
∴ a=52,b=1,c=2 .∴2a+b-c=4. ∴平方根是±2
27.(6分)解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
28.(8分)解:(1)甲车到B站用时false(小时)=16(分钟).
乙车到B站用时false(小时)=8(分钟).
(用小时或分钟表示均可)
(2)由题意可列方程false
解得:false小时=14分钟.
所以8:14两车相遇.
(3)分三种情况:
①两车相遇前,乙车刚到B站时,两车相距4千米,此时false(小时)
②两车相遇后,乙车经过B站,甲车还没有到B站时,false,
解得:false,此时甲车已经过B站,与假设矛盾(舍去).
③两车相遇后,甲乙两车都经过B站时,false,
解得∶false(小时)
综上所述,当false小时或false小时时,两车相距4千米.
一.选择题(每题2分,共20分)
1.﹣2020的相反数为( )
A.﹣ B.2020 C.﹣2020 D.
2.在π,,0,0.3,﹣,,3.121121112…(每两个2之间依次多一个1)中,无理数的个数有( )
A.5个 B.4个 C.3个 D.2个
3.2020年11月1日第七次全国人口普查在全国范围内展开.国家统计局表示,截止2019年底,中国大陆总人口为14.05亿,将14.05亿用科学记数法表示为( )
A.false B.false C.false D.false
4.如图,∠1和∠2不是同旁内角的是( )
A. B. C. D.
5.已知关于x的方程2x+8=﹣6与方程2x﹣3a=﹣5的解相同,则a的值为( )
A.13 B.3 C.﹣3 D.8
6.下列等式的变形中,正确的是( )
A.如果false,那么a=b B.如果∣a∣=∣b∣,那么a=b
C.如果ax =ay,那么x= y D.如果a=b,那么false
7.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2 ②∠1=∠3 ③∠2=∠4
④∠DAB+∠ABC=180° ⑤∠BAD+∠ADC=180°.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
8.若多项式2x2﹣3y的值为2,则多项式6x2﹣9y﹣10的值为( )
A.4 B.﹣6 C.﹣8 D.﹣4
9.如图①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图②所示,再将剪下的两个小长方形拼成一个新的长方形,如图③所示,则新长方形的周长可表示为( )
A.4a﹣8b B.2a﹣3b C.2a﹣4b D.4a﹣10b
10.如图,线段 CD在线段 AB上,且 CD=1,若线段AB的长度是一个正整数,则图中以A,
B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分,共30分)
11.如果把“向东走2米”记作“+2米”,那么“向西走5米”应该记作 米.
12.单项式﹣的系数是 ,次数是 .
13.0.47249≈ (精确到千分位).
一种商品每件成本是a元,原来按成本增加20%定出价格进销售,一段时间后,由于库存积压减价,按原价的9折出售,则现在每件售价为 元.
若实数a,b满足|a﹣2|+(b+3)2=0,则ba= .
16.若方程的解为则方程组的解为 .
17.已知A 、O、B 三点共线,∠BOC=35°,作 OD⊥OC,则∠DOB=___▲____
18.如图,已知∠1=(3x+24)°,∠2=(5x+20)°,要使m∥n,那么∠1= .
19.已知整数a1,a2,a3,a4,…满足下列条件∶a1=0,a2=-∣a1+1∣,a3=-∣a2+2∣,
a4=-∣a3+3∣,a5 =-∣a4+4∣,…,依此类推,则a2020的值为____
将边长为1的正方形纸片按图1所示方法进行对折,第1次对折后得到的图形面积为s1,第2次对折后得到的图形面积为s2,…,第n次对折后得到的图形面积为sn,请根据图2化简:s1+s2+s3+…+s2020= .
三、解答题:(共50分)
21.(6分)计算:
(1)8+(﹣11)﹣|﹣5|; (2)﹣92.
22.(6分)解方程(组):
(1)false (2)
(6分)化简求值:5(3a2b﹣2ab2)﹣4(﹣2ab2+3a2b),其中a=﹣2,b=1.
24.(6分)如图所示,已知点A,B,C,D,请按要求画出图形
(1)画直线AB和射线CB;
(2)连结AC,并在直线AB上用直尺和圆规作线段AE,使AE=2AC(要求保留作图痕迹);
(3)在直线AB上确定一点P,使PC+PD的和最短,并写出画图的依据。
25.(6分)给出定义如下:
若有理数a,b满足等式a+b=ab﹣1,则我们称a,b为一对“伴生有理数”,记为(a,b).例如:2+3=2×3﹣1,则称2,3是一对“伴生有理数”,记为(2,3).
(1)判断(,﹣3)、(7,)是否为“伴生有理数”,请说明理由;
(2)若(4,m)为“伴生有理数”,求m的值.
26.(6分)解关于x,y的方程组 false 时,甲正确地解出 false ,乙因为把c抄错了,误解为 false ,求2a+b—c的平方根.
27.(6分)如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
28.(8分)如图,城乡公交车行驶在笔直的公路上,这条路上有A,B,C三个站点,已知相邻两站之间的距离分别为false千米,false千米,且每个站点的停靠时间为4分钟.已知甲、乙两车于上午8:00分别从A站,C站出发相向而行,两车的速度均为30千米/小时,设两车出发t小时后,问:
(1)甲、乙两车到达B站分别用时多少?
(2)求两车相遇的时刻.
(3)当两车相距4千米时,求t的值.
七年级数学试卷参考答案
选择题:本题有10小题,每小题2分,共20分.
BCCDC ADDAB
二、填空题:本题有10小题,每小题3分,共30分.
11.-5 12.,3 13.0.472 14.1.08a 15.9
396938512065016 .false 17.1250或550 18.750 19.-1010 20. 2020
三、解答题:本题有8小题,共50分.
21.(6分)(1)-8 (2)false
22.(6分)(1)false (2)falsefalse
23.(6分)3a2b-2ab2 ; 16
24.(6分)画图略 理由:两点之间,线段最短
25(6分).解:(1)∵﹣3=﹣,×(﹣3)﹣1=﹣,
∴﹣3=×(﹣3)﹣1,
∴(,﹣3)是“伴生有理数”,
∵7+=,7×﹣1=,
∴7+≠7×﹣1,
∴(7,)不是“伴生有理数”;
(2)由题意得:4+m=4m﹣1,
解得m=.
故m的值.
26.(6分) 把 x=2,y=4 代入方程 3x?cy=?2 ,得:
6?4c=?2 ,
解得: c=2 .
把 {x=2y=4,{x=4y=?1 分别代入方程 ax+by=9 ,得:
{2a+4b=94a?b=9 ,
解得 :{a=52b=1 .
∴ a=52,b=1,c=2 .∴2a+b-c=4. ∴平方根是±2
27.(6分)解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
28.(8分)解:(1)甲车到B站用时false(小时)=16(分钟).
乙车到B站用时false(小时)=8(分钟).
(用小时或分钟表示均可)
(2)由题意可列方程false
解得:false小时=14分钟.
所以8:14两车相遇.
(3)分三种情况:
①两车相遇前,乙车刚到B站时,两车相距4千米,此时false(小时)
②两车相遇后,乙车经过B站,甲车还没有到B站时,false,
解得:false,此时甲车已经过B站,与假设矛盾(舍去).
③两车相遇后,甲乙两车都经过B站时,false,
解得∶false(小时)
综上所述,当false小时或false小时时,两车相距4千米.
同课章节目录
