鲁教版数学六年级下册期中测试题二(含答案)
文档属性
| 名称 | 鲁教版数学六年级下册期中测试题二(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:38:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
鲁教版数学六年级下册期中测试题(二)
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.下列计算,正确的是( )
A.a5+a5=a10 B.(2a2)3=6a6 C.a8÷a2=a4 D.(a3)4=a12
2.下列说法正确的是( )
A.画一条长为3cm的射线 B.射线、线段、直线中直线最长
C.射线是直线的一部分 D.延长直线AB到C
3.能用∠1、∠EOF、∠O三种方法表示同一个角的图形是( )
4.原子是构成自然界各种元素的基本单位,由原子核和核外轨道电子组成原子的直径只有0.1纳米(1纳米=0.000001毫米).“0.1纳米”用科学记数法表示为( )
A.1.0×10-7毫米 B.1.0×10-6毫米 C.1.0×10-5毫米 D.10×10-6毫米
5.如图所示,点D在线段ABA上,AD:BD=1:2,点C是AB的中点,若DC=3,
则线段AB的长是( )
A.18 B.12 C.16 D.14
6.如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的度数为( )
A.45° B.30° C.25° D.20°
7.一架飞机从某机场向南偏东50°方向飞行了2300km返回时飞机应向( )
A.北偏西50°方向飞行2300km B.北偏西40°方向飞行2300km
C.南偏东50°方向飞行2300km D.南偏东40°方向飞行2300km
8.在-12,(x-3.14)0,2-1,0这四个数中,最小的数是( )
A.-12 B.(x-3.14)0 C.2-1 D.0
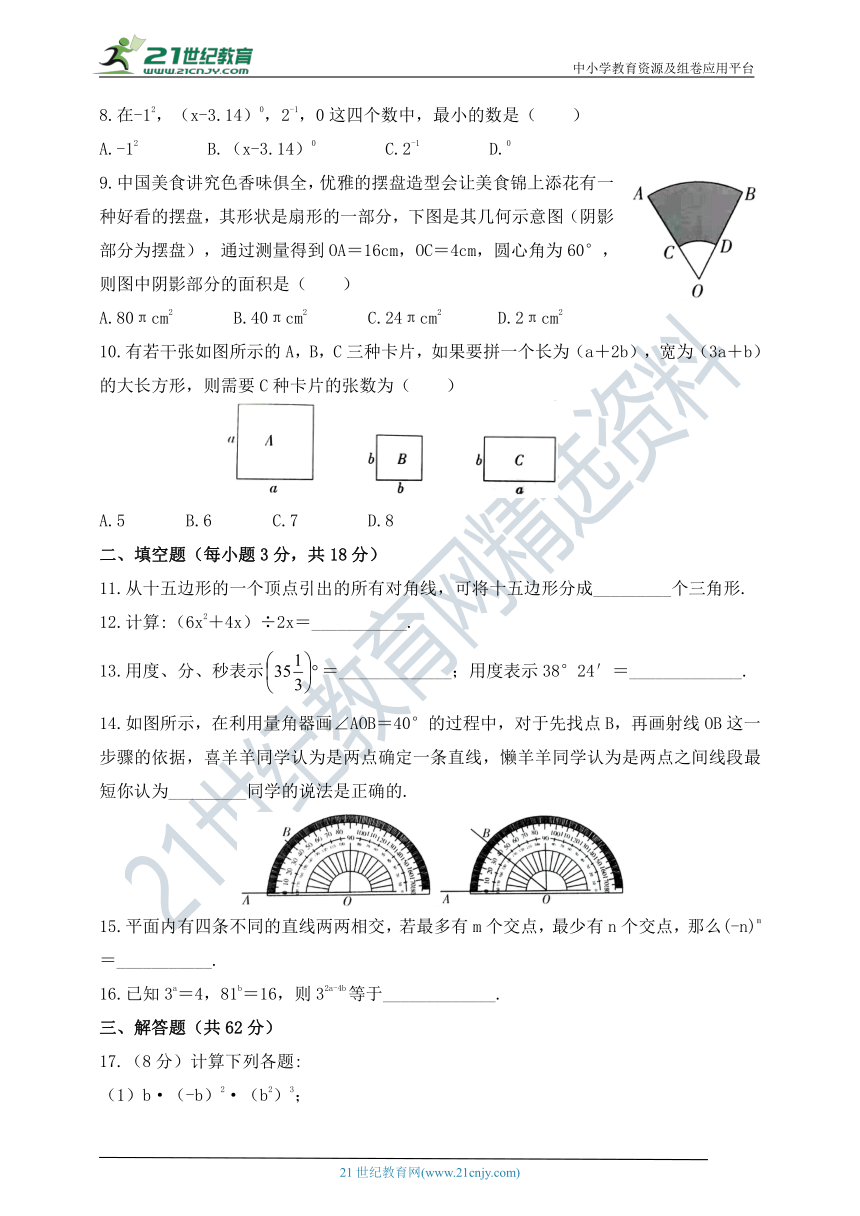
9.中国美食讲究色香味俱全,优雅的摆盘造型会让美食锦上添花有一种好看的摆盘,其形状是扇形的一部分,下图是其几何示意图(阴影部分为摆盘),通过测量得到OA=16cm,OC=4cm,圆心角为60°,则图中阴影部分的面积是( )
A.80πcm2 B.40πcm2 C.24πcm2 D.2πcm2
10.有若干张如图所示的A,B,C三种卡片,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C种卡片的张数为( )
A.5 B.6 C.7 D.8
二、填空题(每小题3分,共18分)
11.从十五边形的一个顶点引出的所有对角线,可将十五边形分成_________个三角形.
12.计算:(6x2+4x)÷2x=___________.
13.用度、分、秒表示=_____________;用度表示38°24′=_____________.
14.如图所示,在利用量角器画∠AOB=40°的过程中,对于先找点B,再画射线OB这一步骤的依据,喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短你认为_________同学的说法是正确的.
15.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(-n)m=___________.
16.已知3a=4,81b=16,则32a-4b等于_____________.
三、解答题(共62分)
17.(8分)计算下列各题:
(1)b·(-b)2·(b2)3;
(2)-2x2y(3xy2z-2y2z);
(3)[(x+1)(x+2)-2]÷x;
(4)(利用整式的乘法公式)799×801+1.
18.(8分)若(x2+nx+3)(x2-3x+m)的结果中不含x2项和x3项,求m,n的值.
19.(10分)如图所示,已知∠AOB=120°,在∠AOB内画射线OC,∠AOC=40°.
(1)如图①,求∠BOC的度数;
(2)如图②,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
20.(12分)一个圆被分割成四个扇形,它们的圆心角的度数比为2:3:4:3.
(1)求这四个扇形的圆心角的度数;
(2)若圆的半径为2cm,请求出这四个扇形的面积.
21.(12分)阅读材料:
求x2+6x+11的最小值.
解:x2+6x+11=x2+6x+9+2=(x+3)2+2,
由于(x+3)2的值为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.
解决问题:
(1)若m2+2mn+2n2(m)-6n+9=0,求的值;
(2)对于多项式x2+y2-2x+2y+5,当x,y取何值时有最小值?
22.(12分)如图所示,相距10千米的A、B两地间有一条笔直的路,C地位于A、B两地之间且距A地4千米.小明同学步行从A地出发以每小时5千米的速度向B地匀速行走,到达B地后立即按原来的速度返回,到达A地后停止设步行时间为t(时),小明的位置为点P.
(1)当t=0.5时,求点P、C间的距离;
(2)当小明距离C地1千米时,直接写出所有满足条件的t值;
(3)在整个步行过程中,求点P与点A的距离(用含t的代数式表示)
参考答案
一、选择题
1.D 2.C 3.D 4.A 5.A 6.B 7.A 8.A 9.B 10.C
二、填空题
11. 13 12. 3x+2 13. 35°20′;38.4° 14. 喜羊羊
15. 1 16. 1
三、解答题
17.解析(1)原式=b·b2·b6=b9
(2)原式=-6x3y3+4x2y3z
(3)原式=(x2+3x+2-2)÷x=x+3
(4)原式=(800-1)(800+1)+1=8002-1+1=60000.
18.解析(x2+nx+3)(x2-3x+m)
=x4+nx3+3x2-3x3-3nx2-9x+mx2+mnx+3m
=x4+(n-3)x3+(3-3n+m)x2+(mn-9)x+3m
因为结果中不含x2项和x3项,
所以3-3n+m=0,n-3=0,解得m=6,n=3.
19.解析(1)因为∠AOB=120°,∠AOC=40°,
所以∠BOC=∠AOB-∠AOC=120°-40°=80°
(2)因为OD平分∠AOC,所以∠AOD=∠COD=∠AOC,
因为OE平分∠BOC,所以∠BOE=∠COE=∠BOC,
所以∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=∠AOB=×120°=60°.
20.解析(1)因为一个圆被分割成四个扇形,它们的圆心角的度数的比为2:3:4:3,所以它们的圆心角的度数分别为
,,,
.
(2)因为圆的半径为2 cm,所以四个扇形的面积分别为
(cm2),(cm2),
(cm2),(cm2).
21.解析(1)因为m2+2mn+2n2-6n+9=0,所以m2+2mn+n2+n2-6n+9=0,
所以(m+n)2+(n-3)2=0,所以m+n=0且n-3=0,
所以m=-3,n=3,
所以=.
(2)原式=
x2+y2-2x+2y+1+1+3=(x2-2x+1)+(y2+2y+1)+3=(x-1)2+(y+1)2+3,
因为(x-1)2和(y+1)2的值为非负数,
所以当x=1,y=-1时,x2+y2-2x+2y+5有最小值.
22.解析(1)由题意得,小明同学的速度=5km/h,AC=4km,aB=10km,
当t=0.5时,5×0.5=2.5km,即AP=2.5km,
所以PC=AC-AP=4-2.5=1.5km.即点P、C间的距离为1.5km.
(2)当小明距离C地1km时,t的值是0.6或1或3或3.4.
(3)小明从A地步行到B地的过程中,AP=5tkm,
小明从B地步行到A地的过程中,AP=(20-5t)km.
_21?????????è?????(www.21cnjy.com)_
鲁教版数学六年级下册期中测试题(二)
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.下列计算,正确的是( )
A.a5+a5=a10 B.(2a2)3=6a6 C.a8÷a2=a4 D.(a3)4=a12
2.下列说法正确的是( )
A.画一条长为3cm的射线 B.射线、线段、直线中直线最长
C.射线是直线的一部分 D.延长直线AB到C
3.能用∠1、∠EOF、∠O三种方法表示同一个角的图形是( )
4.原子是构成自然界各种元素的基本单位,由原子核和核外轨道电子组成原子的直径只有0.1纳米(1纳米=0.000001毫米).“0.1纳米”用科学记数法表示为( )
A.1.0×10-7毫米 B.1.0×10-6毫米 C.1.0×10-5毫米 D.10×10-6毫米
5.如图所示,点D在线段ABA上,AD:BD=1:2,点C是AB的中点,若DC=3,
则线段AB的长是( )
A.18 B.12 C.16 D.14
6.如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC,则∠AOC的度数为( )
A.45° B.30° C.25° D.20°
7.一架飞机从某机场向南偏东50°方向飞行了2300km返回时飞机应向( )
A.北偏西50°方向飞行2300km B.北偏西40°方向飞行2300km
C.南偏东50°方向飞行2300km D.南偏东40°方向飞行2300km
8.在-12,(x-3.14)0,2-1,0这四个数中,最小的数是( )
A.-12 B.(x-3.14)0 C.2-1 D.0
9.中国美食讲究色香味俱全,优雅的摆盘造型会让美食锦上添花有一种好看的摆盘,其形状是扇形的一部分,下图是其几何示意图(阴影部分为摆盘),通过测量得到OA=16cm,OC=4cm,圆心角为60°,则图中阴影部分的面积是( )
A.80πcm2 B.40πcm2 C.24πcm2 D.2πcm2
10.有若干张如图所示的A,B,C三种卡片,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C种卡片的张数为( )
A.5 B.6 C.7 D.8
二、填空题(每小题3分,共18分)
11.从十五边形的一个顶点引出的所有对角线,可将十五边形分成_________个三角形.
12.计算:(6x2+4x)÷2x=___________.
13.用度、分、秒表示=_____________;用度表示38°24′=_____________.
14.如图所示,在利用量角器画∠AOB=40°的过程中,对于先找点B,再画射线OB这一步骤的依据,喜羊羊同学认为是两点确定一条直线,懒羊羊同学认为是两点之间线段最短你认为_________同学的说法是正确的.
15.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(-n)m=___________.
16.已知3a=4,81b=16,则32a-4b等于_____________.
三、解答题(共62分)
17.(8分)计算下列各题:
(1)b·(-b)2·(b2)3;
(2)-2x2y(3xy2z-2y2z);
(3)[(x+1)(x+2)-2]÷x;
(4)(利用整式的乘法公式)799×801+1.
18.(8分)若(x2+nx+3)(x2-3x+m)的结果中不含x2项和x3项,求m,n的值.
19.(10分)如图所示,已知∠AOB=120°,在∠AOB内画射线OC,∠AOC=40°.
(1)如图①,求∠BOC的度数;
(2)如图②,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
20.(12分)一个圆被分割成四个扇形,它们的圆心角的度数比为2:3:4:3.
(1)求这四个扇形的圆心角的度数;
(2)若圆的半径为2cm,请求出这四个扇形的面积.
21.(12分)阅读材料:
求x2+6x+11的最小值.
解:x2+6x+11=x2+6x+9+2=(x+3)2+2,
由于(x+3)2的值为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.
解决问题:
(1)若m2+2mn+2n2(m)-6n+9=0,求的值;
(2)对于多项式x2+y2-2x+2y+5,当x,y取何值时有最小值?
22.(12分)如图所示,相距10千米的A、B两地间有一条笔直的路,C地位于A、B两地之间且距A地4千米.小明同学步行从A地出发以每小时5千米的速度向B地匀速行走,到达B地后立即按原来的速度返回,到达A地后停止设步行时间为t(时),小明的位置为点P.
(1)当t=0.5时,求点P、C间的距离;
(2)当小明距离C地1千米时,直接写出所有满足条件的t值;
(3)在整个步行过程中,求点P与点A的距离(用含t的代数式表示)
参考答案
一、选择题
1.D 2.C 3.D 4.A 5.A 6.B 7.A 8.A 9.B 10.C
二、填空题
11. 13 12. 3x+2 13. 35°20′;38.4° 14. 喜羊羊
15. 1 16. 1
三、解答题
17.解析(1)原式=b·b2·b6=b9
(2)原式=-6x3y3+4x2y3z
(3)原式=(x2+3x+2-2)÷x=x+3
(4)原式=(800-1)(800+1)+1=8002-1+1=60000.
18.解析(x2+nx+3)(x2-3x+m)
=x4+nx3+3x2-3x3-3nx2-9x+mx2+mnx+3m
=x4+(n-3)x3+(3-3n+m)x2+(mn-9)x+3m
因为结果中不含x2项和x3项,
所以3-3n+m=0,n-3=0,解得m=6,n=3.
19.解析(1)因为∠AOB=120°,∠AOC=40°,
所以∠BOC=∠AOB-∠AOC=120°-40°=80°
(2)因为OD平分∠AOC,所以∠AOD=∠COD=∠AOC,
因为OE平分∠BOC,所以∠BOE=∠COE=∠BOC,
所以∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=∠AOB=×120°=60°.
20.解析(1)因为一个圆被分割成四个扇形,它们的圆心角的度数的比为2:3:4:3,所以它们的圆心角的度数分别为
,,,
.
(2)因为圆的半径为2 cm,所以四个扇形的面积分别为
(cm2),(cm2),
(cm2),(cm2).
21.解析(1)因为m2+2mn+2n2-6n+9=0,所以m2+2mn+n2+n2-6n+9=0,
所以(m+n)2+(n-3)2=0,所以m+n=0且n-3=0,
所以m=-3,n=3,
所以=.
(2)原式=
x2+y2-2x+2y+1+1+3=(x2-2x+1)+(y2+2y+1)+3=(x-1)2+(y+1)2+3,
因为(x-1)2和(y+1)2的值为非负数,
所以当x=1,y=-1时,x2+y2-2x+2y+5有最小值.
22.解析(1)由题意得,小明同学的速度=5km/h,AC=4km,aB=10km,
当t=0.5时,5×0.5=2.5km,即AP=2.5km,
所以PC=AC-AP=4-2.5=1.5km.即点P、C间的距离为1.5km.
(2)当小明距离C地1km时,t的值是0.6或1或3或3.4.
(3)小明从A地步行到B地的过程中,AP=5tkm,
小明从B地步行到A地的过程中,AP=(20-5t)km.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
