高一数学人教A版必修5第一章1.2 应用举例(1)课件(共19张PPT)
文档属性
| 名称 | 高一数学人教A版必修5第一章1.2 应用举例(1)课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 954.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 18:09:36 | ||
图片预览





文档简介
用木棍测量金字塔的高度
泰勒斯(约公元前624年 --- 约公元前546年),古希腊第一位闻名世界的大数学家.
人教A版必修5第一章解三角形
1.2 应用举例
(测量高度问题)
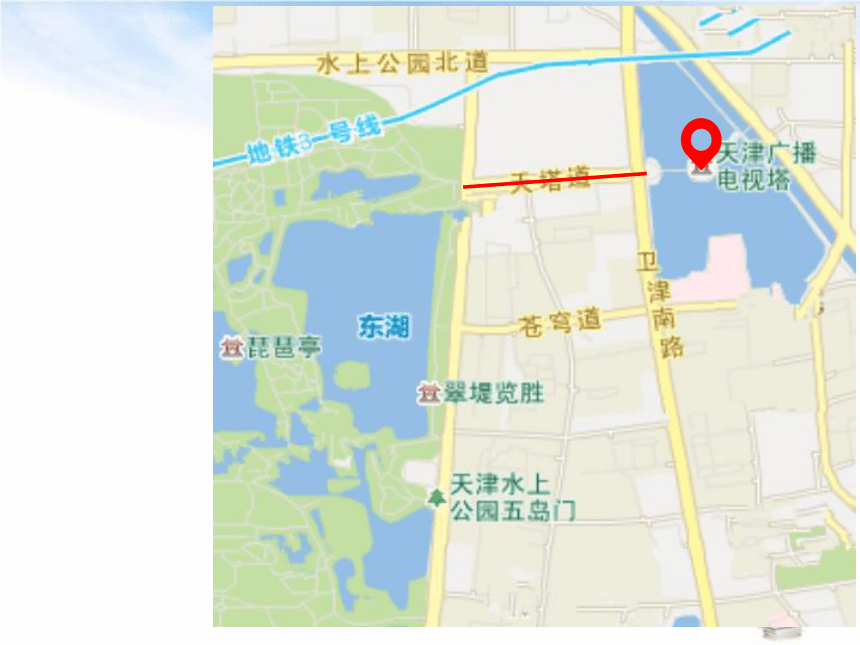
测量任务
天塔是天津广播电视塔的简称,总高度415.2米,为世界第四、亚洲第二高塔,耸立于碧波与云霄之间,是世界上唯一一座“水中之塔”,其势如剑倚天,享有“天塔旋云”之美称。
小组测量任务展示
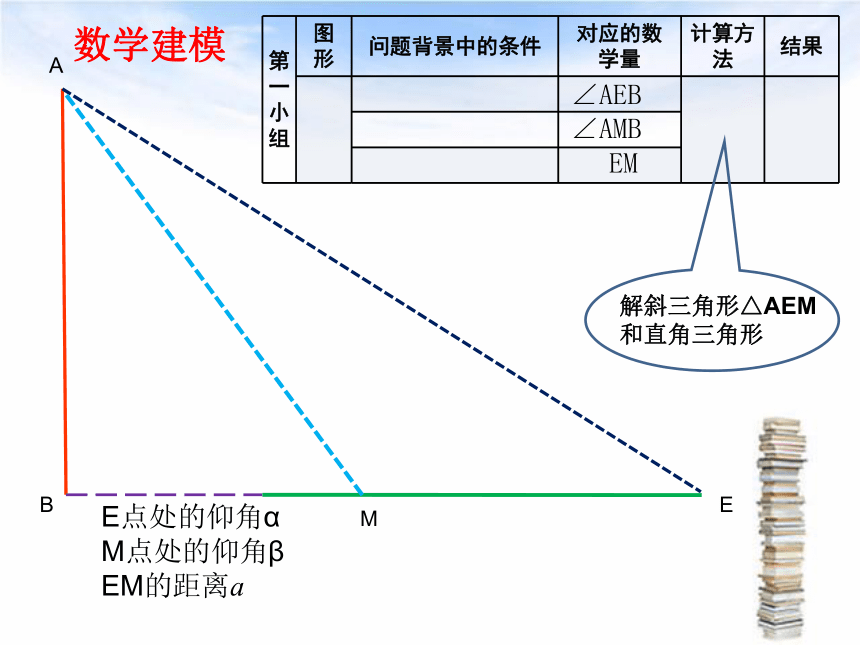
第一小组
A
B
E
第一小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
M
E点处的仰角α
M点处的仰角β
EM的距离a
∠AEB
∠AMB
EM
解斜三角形△AEM和直角三角形
数学建模
第二小组
A
B
E
M
可以测量:E点处的仰角α,M点处的仰角β,EM的距离为
a,∠EBM=θ
第二小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
数学建模
第三小组
可以测量:E点处的仰角α,M点处的仰角β,EM的高度为a
A
B
E
M
α
β
第三小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
数学建模
测量底部不可到达的建筑物高度
选择建筑物顶部和地面两个点建立三角形
测量底部不可到达的建筑物高度
选择建筑物顶部和地面两个点建立三角形
测量地面两个点到顶部的仰角
测量地面两个点间的距离、张角等
数学运算
小结:
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
数学建模
小组评价:
天塔总高度415.2米
课堂反馈:
1.在地面上一点D测得一电视塔尖的仰角为45°,再向塔底方向前进100m,又测得塔尖的仰角为60°,则此电视塔高约为( )m.
A.237 B.227 C.247 D.257
2. 在一栋20米高的楼顶测得对面一塔顶的仰角为60°,塔底的俯角为45°,则塔的高度为( )米.
A
作业:
补充练习(选作)
P15,练习1~3
完善实验报告
泰勒斯(约公元前624年 --- 约公元前546年),古希腊第一位闻名世界的大数学家.
人教A版必修5第一章解三角形
1.2 应用举例
(测量高度问题)
测量任务
天塔是天津广播电视塔的简称,总高度415.2米,为世界第四、亚洲第二高塔,耸立于碧波与云霄之间,是世界上唯一一座“水中之塔”,其势如剑倚天,享有“天塔旋云”之美称。
小组测量任务展示
第一小组
A
B
E
第一小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
M
E点处的仰角α
M点处的仰角β
EM的距离a
∠AEB
∠AMB
EM
解斜三角形△AEM和直角三角形
数学建模
第二小组
A
B
E
M
可以测量:E点处的仰角α,M点处的仰角β,EM的距离为
a,∠EBM=θ
第二小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
数学建模
第三小组
可以测量:E点处的仰角α,M点处的仰角β,EM的高度为a
A
B
E
M
α
β
第三小组
图形
问题背景中的条件
对应的数学量
计算方法
结果
数学建模
测量底部不可到达的建筑物高度
选择建筑物顶部和地面两个点建立三角形
测量底部不可到达的建筑物高度
选择建筑物顶部和地面两个点建立三角形
测量地面两个点到顶部的仰角
测量地面两个点间的距离、张角等
数学运算
小结:
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
数学建模
小组评价:
天塔总高度415.2米
课堂反馈:
1.在地面上一点D测得一电视塔尖的仰角为45°,再向塔底方向前进100m,又测得塔尖的仰角为60°,则此电视塔高约为( )m.
A.237 B.227 C.247 D.257
2. 在一栋20米高的楼顶测得对面一塔顶的仰角为60°,塔底的俯角为45°,则塔的高度为( )米.
A
作业:
补充练习(选作)
P15,练习1~3
完善实验报告
