2020-2021学年七年级数学青岛版下册《第8章 角》单元综合培优提升训练(Word版 附答案)
文档属性
| 名称 | 2020-2021学年七年级数学青岛版下册《第8章 角》单元综合培优提升训练(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 11:45:25 | ||
图片预览




文档简介
青岛版2021年度七年级数学下册《第8章 角》单元综合培优提升训练(附答案)
1.如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠COE=28°,则∠AOD的度数为( )
A.56° B.62° C.72° D.124°
2.在所给的:①15°、②65°、③75°、④135°、⑤145°的角中,可以用一副三角板画出来的是( )
A.②④⑤ B.①②④ C.①③⑤ D.①③④
3.上午8点整时,钟表表面的时针与分针的夹角是( )
A.30° B.45° C.90° D.120°
4.如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中
①90°﹣∠α;②∠β﹣90°③(∠α+∠β)④(∠β﹣∠α)
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,O是直线AB上一点,OE平分∠AOB,∠COD=90°.则图中互余的角、互补的角各有( )对.
A.3,3 B.4,7 C.4,4 D.4,5
6.若∠1与∠2互余,∠2与∠3互补,则∠1与∠3的关系是( )
A.∠1=∠3 B.∠1与∠3互余 C.∠1与∠3互补 D.∠3﹣∠1=90°
7.通常我们把时钟的时针与分针所成的角叫做钟面角,若某整点时刻,钟面角∠α恰好是∠α的补角的2倍,此时对应的时间应是( )
A.8点 B.4点 C.6点 D.8点或4点
8.已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( )
A.20° B.40° C.20°或40° D.30°或10°
9.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON的大小是( )
A.45° B.45°+∠AOC C.60°﹣∠AOC D.90°﹣∠AOC
10.一副三角板,如图所示叠放在一起,则∠AOB+∠COD=( )
A.180° B.150° C.160° D.170°
11.如图,从O点引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=80°,∠EOF=160°,OE、OF分别是∠AOD、∠BOC的平分线.则∠COD的度数为 度.
12.如图,已知OA⊥OB于点O,∠BOC=20°20′,那么∠AOC= ° ′.
13.从点O引出三条射线OA,OB,OC,已知∠AOB=30°,在这三条射线中,当其中一条射线是另两条射线所组成角的平分线时,则∠AOC= °
14.已知一个角的补角是它的余角的4倍,那么这个角的度数是 .
15.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
16.计算:48°39′+67°31′= .
17.已知OC平分∠AOB,若∠AOB=70°,∠COD=10°,则∠AOD的度数为 .
18.若∠AOB=75°,∠AOC=27°,则∠BOC= .
19.如图,∠AOC和∠BOD都是直角,且∠DOC=30°,OM是∠DOC平分线,ON是∠COB的平分线,则∠MON的度数是 .
20.以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=17°,∠AOP的度数为 .
21.如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.
(1)求∠AOE的度数;
(2)写出图中与∠EOC互余的角;
(3)∠COE有补角吗?若有,请把它找出来,并说明理由.
22.如图,直线AB、CD相交于点O,OA是∠EOC的平分线,∠EOD=100°,
(1)请指出∠BOC的一个补角;
(2)求出∠BOD的度数.
23.如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
24.如图所示,∠AOB=90°,OE是∠AOC的平分线,OD是∠BOC的平分线,若∠BOC=30°.求:
(1)∠DOE的度数;
(2)若没有绘出∠BOC的度数,你能否求出∠DOE的度数?请说明理由;
(3)在(2)的条件下,若∠AOB=α,求∠DOE的度数,你能从中发现什么规律?
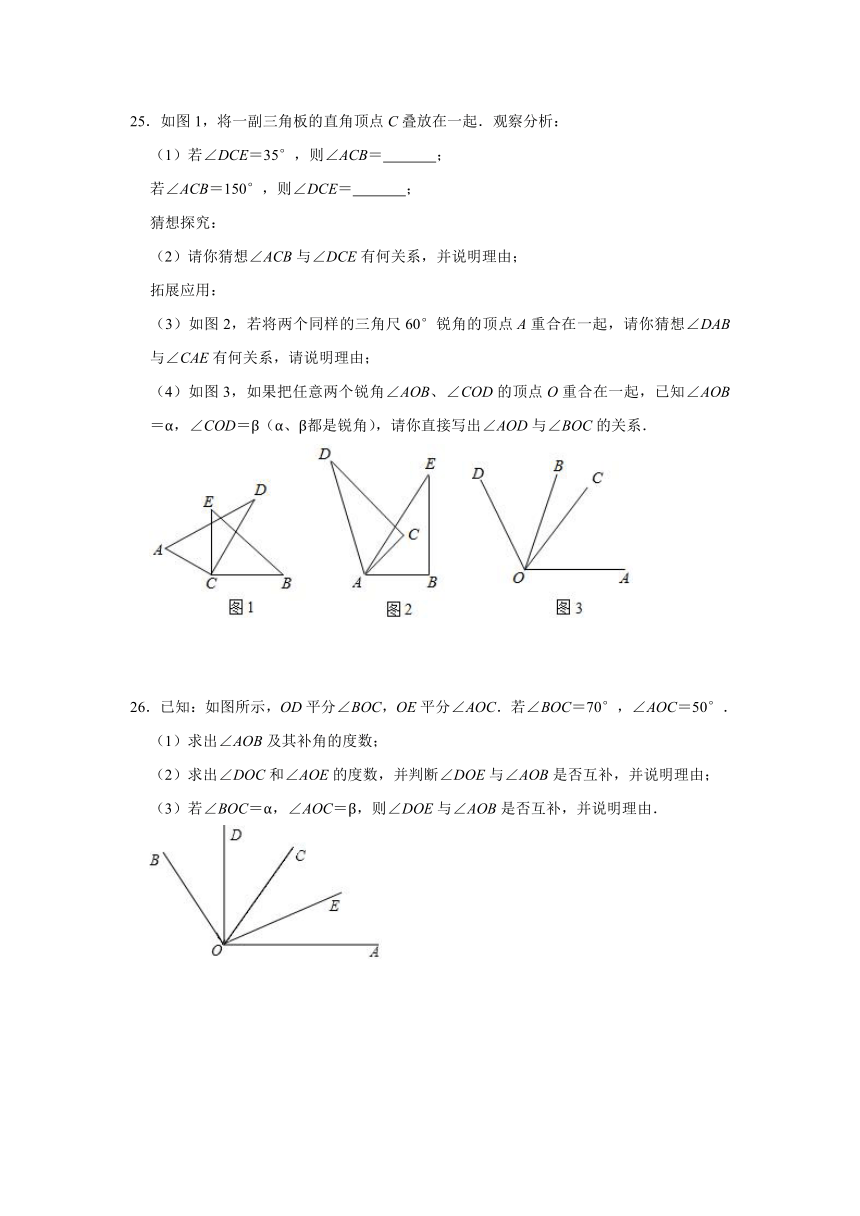
25.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB= ;
若∠ACB=150°,则∠DCE= ;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
26.已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE与∠AOB是否互补,并说明理由.
27.学习千万条,思考第一条.请你用本学期所学知识探究以下问题:
Ⅰ.已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)如图1,三角板的一边ON与射线OB重合,且∠AOC=150°,若以点O为观察中心,射线OM表示正北方向,求射线OC表示的方向;
(2)如图2,将三角板放置到如图位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数.
Ⅱ.已知点A、O、B不在同一条直线上,∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的式子表示∠MON的大小.
参考答案
1.解:∵OE平分∠BOC,
∴∠BOC=2∠COE=56°.
∴∠AOC=180°﹣∠BOC=124°.
∵OD平分∠AOC,
∴∠AOD=∠COD=∠AOC=62°.
故选:B.
2.解:①45°﹣30°=15°,可以用一副三角板画出来;
②65°不可以用一副三角板画出来;
③45°+30°=75°,可以用一副三角板画出来;
④90°+45°=135°,可以用一副三角板画出来;
⑤145°不可以用一副三角板画出来;
故选:D.
3.解:如图,上午8点整时,钟表表面的时针与分针的夹角是4×30°=120°
故选:D.
4.解:∵∠α和∠β互补,
∴∠α+∠β=180°,
∴∠α=180°﹣∠β,
于是有:
∠α的余角为:90°﹣∠α,故①正确,
∠α的余角为:90°﹣∠α=90°﹣(180°﹣∠β)=∠β﹣90°,故②正确,
∠α的余角为:90°﹣∠α=∠α+∠β﹣∠α=∠β﹣∠α,故④正确,
而(∠α+∠β)=90°,而∠α不一定是直角,因此③不正确,
因此正确的有①②④,
故选:C.
5.解:∵OE平分∠AOB,
∴∠AOE=∠BOE=90°,
∴互余的角有∠AOC和∠COE,∠AOC和∠BOD,∠COE和∠DOE,∠DOE和∠BOD共4对,
互补的角有∠AOC和∠BOC,∠DOE和∠BOC,∠COE和∠AOD,∠BOD和∠AOD,∠AOE和∠BOE,∠AOE和∠COD,∠COD和∠BOE共7对.
故选:B.
6.解:由题意得,①∠1+∠2=90°,②∠2+∠3=180°
②﹣①得,∠3﹣∠1=180°﹣90°=90°,
故选:D.
7.解:根据题意有∠α=2(180﹣∠α),
解得∠α=120°,
则此时对应的时间应是8点或4点.
故选:D.
8.
解:∠BOC在∠AOB内部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°;
∠BOC在∠AOB外部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB+∠BON=30°+10°=40°.
故选:C.
9.解:∵OM平分∠BOC,ON平分∠AOC,
∴∠MOC=∠BOC,∠NOC=∠AOC,
∴∠MON=∠MOC﹣∠NOC=(∠BOC﹣∠AOC)=∠BOA=90°=45°.
故选:A.
10.解:由已知,得∠AOC=90°,∠BOD=90°,∴∠AOB+∠COD=∠AOD+∠COD+∠BOC+∠COD=∠AOC+∠BOD=180°.
故选:A.
11.解:设∠AOE=α,∠BOF=β,
∵∠AOB=80°,∠EOF=160°,
∴∠AOE+∠BOF=360°﹣∠AOE﹣∠BOF=360°﹣80°﹣160°=120°.
∵OE、OF分别是∠AOD、∠BOC的平分线.
∴∠AOD=2α,∠BOC=2β.
∴∠COD=360°﹣∠AOB﹣∠AOD﹣∠BOC=360°﹣80°﹣120°×2=40°.
故答案为40.
12.解:∵OA⊥OB,
∴∠AOB=90°,
∵∠BOC=20′20′,
∴∠AOC=90°﹣20°20′=69°40′,
故答案为:69,40.
13.解:①当OC平分∠AOB时,∠AOC=∠AOB=15°;
②当OA平分∠BOC时,∠AOC=∠AOB=30°;
③当OB平分∠AOC时,∠AOC=2∠AOB=60°.
故答案为:15或30或60.
14.解:设这个角为x,则补角为(180°﹣x),余角为(90°﹣x),
由题意得,4(90°﹣x)=180°﹣x,
解得:x=60,即这个角为60°.
故答案为:60°.
15.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,故答案为:42.
16.解:39′+31′=70′=1°10′,
故48°39′+67°31′=116°10'.
故答案为:116°10'.
17.解:(1)若射线OD在OC的下方时,
如图1所示:
∵OC平分∠AOB,
∴∠AOC=,
又∵∠AOB=70°,
∴∠AOC==35°,
又∵∠AOC=∠COD+∠AOD,
∠COD=10°,
∴∠AOD=35°﹣10°=25°;
(2)若射线OD在OC的上方时,
如图2所示:
同(1)可得:∠AOC=35°,
又∵∠AOD=∠AOC+∠COD,
∴∠AOD=35°+10°=45°;
综合所述∠AOD的度数为25°或45°,
故答案为25°或45°.
18.解:(1)射线OC在∠AOB的内部时,
如图1所示:
∵∠AOB=75°,∠AOC=27°,
∠AOB=∠AOC+∠BOC,
∴∠BOC=∠AOB﹣∠AOC=75°﹣27°=48°;
(2)射线OC在∠AOB的外部时,
如图2所示:
∵∠AOB=75°,∠AOC=27°,
∠BOC=∠AOB+∠AOC,
∴∠BOC=75°+27°=102°,
综合所述,∠BOC的度数为48°或102°,
故答案为48°或102°.
19.解:∵OM是∠DOC平分线,ON是∠COB的平分线,
∴∠COM=∠DOM=∠COD,∠BON=∠CON=∠BOC,
∵∠BOC+∠COD=∠BOD=90°,
∴∠COM+∠CON=∠BOD=45°=∠MON,
故答案为:45°
20.解:如图1,当射线OP在∠AOB的内部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOB=∠AOP+∠BOP=5x=17°,
解得:x=3.4°,
则∠AOP=10.2°;
如图2,当射线OP在∠AOB的外部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOP=∠AOB+∠BOP,
又∵∠AOB=17°,
∴3x=17°+2x,
解得:x=17°,
则∠AOP=51°.
故∠AOP的度数为10.2°或51°.
故答案为:10.2°或51°.
21.解:(1)∵∠BOC=40°,
∴∠AOC=140°,
∵OE是∠AOC的角平分线,
∴∠AOE的度数为:140°÷2=70°;
(2)∵OD、OE分别是∠BOC、∠AOC的角平分线,
∴∠AOE=∠EOC,∠COD=∠BOD,
∴∠EOC+∠COD=90°,
∴∠BOD+∠EOC=90°,
∴图中与∠EOC互余的角有∠COD,∠BOD;
(3)∠COE有补角,
理由:∵∠AOE=∠EOC,∠AOE+∠BOE=180°,
∴∠COE+∠BOE=180°,
∴∠COE有补角是∠BOE.
22.解:(1)∠BOC的补角为:∠AOC(或∠BOD、∠AOE)
(2)根据“同角的补角相等”得∠BOD=∠AOC.
∵∠EOD=100°,∠EOD+∠EOC=180°,
∴∠EOC=180°﹣∠EOD=180°﹣100°=80°,
∵OA是∠EOC的平分线,
∴∠AOC=∠EOC=40°.
∴∠BOD=40°.
23.解:(1)如图,∵OB为∠AOC的平分线,OD是∠COE的平分线,
∴∠AOB=∠BOC,∠DOE=∠DOC,
∴∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°;
(2)如图,∵OD是∠COE的平分线,∠COD=30°,
∴∠EOC=2∠COD=60°.
∵∠AOE=140°,∠AOC=∠AOE﹣∠EOC=80°.
又∵OB为∠AOC的平分线,
∴∠AOB=∠AOC=40°.
24.解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=×120°=60°,
∠COD=∠BOC=×30°=15°,
∴∠DOE=∠COE﹣∠COD=60°﹣15°=45°;
(2)若∠BOC的度数没有给出,则∠AOC=∠AOB+∠BOC=90°+∠BOC,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=×(90°+∠BOC)=45°+∠BOC,
∠COD=∠BOC,
∴∠DOE=∠COE﹣∠COD=45°+∠BOC﹣∠BOC=45°;
(3)由图可知,∠AOC=∠AOB+∠BOC,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=(∠AOB+∠BOC),
∠COD=∠BOC,
∴∠DOE=(∠AOB+∠BOC)﹣∠BOC=∠AOB,
∵∠AOB=α,
∴∠DOE=α.
规律:无论∠BOC的大小如何变化,∠DOE始终为∠AOB的一半.
25.解:(1)(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,=β+∠AOB,=α+β.
26.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°﹣∠AOB=180°﹣120°=60°,
(2)∠DOE与∠AOB互补,理由如下:
∵∠DOC=∠BOC=×70°=35°,∠COE=∠AOC=×50°=25°.
∴∠DOE=∠DOC+∠COE=35°+25°=60°.
∴∠DOE+∠AOB=60°+70°+50°=180°,
∴∠DOE与∠AOB互补.
(3)∠DOE与∠AOB不一定互补,理由如下:
∵∠DOC=∠BOC=α,∠COE=∠AOC=β,
∴∠DOE=∠DOC+∠COE=α+β=(α+β),
∴∠DOE+∠AOB=(α+β)+(α+β)=(α+β),
∵α+β的度数不确定
∴∠DOE与∠AOB不一定互补.
27.解:Ⅰ(1)∵∠MOC=∠AOC﹣∠AOM=150°﹣90°=60°,
∴射线OC表示的方向为北偏东60°;
(2)∵∠BON=2∠NOC,OC平分∠MOB,
∴∠MOC=∠BOC=3∠NOC,
∵∠MOC+∠NOC=∠MON=90°,
∴3∠NOC+∠NOC=90°,
∴4∠NOC=90°,
∴∠BON=2∠NOC=45°,
∴∠AOM=180°﹣∠MON﹣∠BON=180°﹣90°﹣45°=45°;
Ⅱ.如图1:
∵∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=∠AOB=α,∠CON=∠BON=∠COB=β,
∴∠MON=∠BOM+∠CON=,
如图2,
∠MON=∠BOM﹣∠BON=;
如图3,
∠MON=∠BON﹣∠BOM=,
∴∠MON为或或
1.如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠COE=28°,则∠AOD的度数为( )
A.56° B.62° C.72° D.124°
2.在所给的:①15°、②65°、③75°、④135°、⑤145°的角中,可以用一副三角板画出来的是( )
A.②④⑤ B.①②④ C.①③⑤ D.①③④
3.上午8点整时,钟表表面的时针与分针的夹角是( )
A.30° B.45° C.90° D.120°
4.如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中
①90°﹣∠α;②∠β﹣90°③(∠α+∠β)④(∠β﹣∠α)
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,O是直线AB上一点,OE平分∠AOB,∠COD=90°.则图中互余的角、互补的角各有( )对.
A.3,3 B.4,7 C.4,4 D.4,5
6.若∠1与∠2互余,∠2与∠3互补,则∠1与∠3的关系是( )
A.∠1=∠3 B.∠1与∠3互余 C.∠1与∠3互补 D.∠3﹣∠1=90°
7.通常我们把时钟的时针与分针所成的角叫做钟面角,若某整点时刻,钟面角∠α恰好是∠α的补角的2倍,此时对应的时间应是( )
A.8点 B.4点 C.6点 D.8点或4点
8.已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( )
A.20° B.40° C.20°或40° D.30°或10°
9.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON的大小是( )
A.45° B.45°+∠AOC C.60°﹣∠AOC D.90°﹣∠AOC
10.一副三角板,如图所示叠放在一起,则∠AOB+∠COD=( )
A.180° B.150° C.160° D.170°
11.如图,从O点引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=80°,∠EOF=160°,OE、OF分别是∠AOD、∠BOC的平分线.则∠COD的度数为 度.
12.如图,已知OA⊥OB于点O,∠BOC=20°20′,那么∠AOC= ° ′.
13.从点O引出三条射线OA,OB,OC,已知∠AOB=30°,在这三条射线中,当其中一条射线是另两条射线所组成角的平分线时,则∠AOC= °
14.已知一个角的补角是它的余角的4倍,那么这个角的度数是 .
15.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
16.计算:48°39′+67°31′= .
17.已知OC平分∠AOB,若∠AOB=70°,∠COD=10°,则∠AOD的度数为 .
18.若∠AOB=75°,∠AOC=27°,则∠BOC= .
19.如图,∠AOC和∠BOD都是直角,且∠DOC=30°,OM是∠DOC平分线,ON是∠COB的平分线,则∠MON的度数是 .
20.以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=17°,∠AOP的度数为 .
21.如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.
(1)求∠AOE的度数;
(2)写出图中与∠EOC互余的角;
(3)∠COE有补角吗?若有,请把它找出来,并说明理由.
22.如图,直线AB、CD相交于点O,OA是∠EOC的平分线,∠EOD=100°,
(1)请指出∠BOC的一个补角;
(2)求出∠BOD的度数.
23.如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
24.如图所示,∠AOB=90°,OE是∠AOC的平分线,OD是∠BOC的平分线,若∠BOC=30°.求:
(1)∠DOE的度数;
(2)若没有绘出∠BOC的度数,你能否求出∠DOE的度数?请说明理由;
(3)在(2)的条件下,若∠AOB=α,求∠DOE的度数,你能从中发现什么规律?
25.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB= ;
若∠ACB=150°,则∠DCE= ;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
26.已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE与∠AOB是否互补,并说明理由.
27.学习千万条,思考第一条.请你用本学期所学知识探究以下问题:
Ⅰ.已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)如图1,三角板的一边ON与射线OB重合,且∠AOC=150°,若以点O为观察中心,射线OM表示正北方向,求射线OC表示的方向;
(2)如图2,将三角板放置到如图位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数.
Ⅱ.已知点A、O、B不在同一条直线上,∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的式子表示∠MON的大小.
参考答案
1.解:∵OE平分∠BOC,
∴∠BOC=2∠COE=56°.
∴∠AOC=180°﹣∠BOC=124°.
∵OD平分∠AOC,
∴∠AOD=∠COD=∠AOC=62°.
故选:B.
2.解:①45°﹣30°=15°,可以用一副三角板画出来;
②65°不可以用一副三角板画出来;
③45°+30°=75°,可以用一副三角板画出来;
④90°+45°=135°,可以用一副三角板画出来;
⑤145°不可以用一副三角板画出来;
故选:D.
3.解:如图,上午8点整时,钟表表面的时针与分针的夹角是4×30°=120°
故选:D.
4.解:∵∠α和∠β互补,
∴∠α+∠β=180°,
∴∠α=180°﹣∠β,
于是有:
∠α的余角为:90°﹣∠α,故①正确,
∠α的余角为:90°﹣∠α=90°﹣(180°﹣∠β)=∠β﹣90°,故②正确,
∠α的余角为:90°﹣∠α=∠α+∠β﹣∠α=∠β﹣∠α,故④正确,
而(∠α+∠β)=90°,而∠α不一定是直角,因此③不正确,
因此正确的有①②④,
故选:C.
5.解:∵OE平分∠AOB,
∴∠AOE=∠BOE=90°,
∴互余的角有∠AOC和∠COE,∠AOC和∠BOD,∠COE和∠DOE,∠DOE和∠BOD共4对,
互补的角有∠AOC和∠BOC,∠DOE和∠BOC,∠COE和∠AOD,∠BOD和∠AOD,∠AOE和∠BOE,∠AOE和∠COD,∠COD和∠BOE共7对.
故选:B.
6.解:由题意得,①∠1+∠2=90°,②∠2+∠3=180°
②﹣①得,∠3﹣∠1=180°﹣90°=90°,
故选:D.
7.解:根据题意有∠α=2(180﹣∠α),
解得∠α=120°,
则此时对应的时间应是8点或4点.
故选:D.
8.
解:∠BOC在∠AOB内部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°;
∠BOC在∠AOB外部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB+∠BON=30°+10°=40°.
故选:C.
9.解:∵OM平分∠BOC,ON平分∠AOC,
∴∠MOC=∠BOC,∠NOC=∠AOC,
∴∠MON=∠MOC﹣∠NOC=(∠BOC﹣∠AOC)=∠BOA=90°=45°.
故选:A.
10.解:由已知,得∠AOC=90°,∠BOD=90°,∴∠AOB+∠COD=∠AOD+∠COD+∠BOC+∠COD=∠AOC+∠BOD=180°.
故选:A.
11.解:设∠AOE=α,∠BOF=β,
∵∠AOB=80°,∠EOF=160°,
∴∠AOE+∠BOF=360°﹣∠AOE﹣∠BOF=360°﹣80°﹣160°=120°.
∵OE、OF分别是∠AOD、∠BOC的平分线.
∴∠AOD=2α,∠BOC=2β.
∴∠COD=360°﹣∠AOB﹣∠AOD﹣∠BOC=360°﹣80°﹣120°×2=40°.
故答案为40.
12.解:∵OA⊥OB,
∴∠AOB=90°,
∵∠BOC=20′20′,
∴∠AOC=90°﹣20°20′=69°40′,
故答案为:69,40.
13.解:①当OC平分∠AOB时,∠AOC=∠AOB=15°;
②当OA平分∠BOC时,∠AOC=∠AOB=30°;
③当OB平分∠AOC时,∠AOC=2∠AOB=60°.
故答案为:15或30或60.
14.解:设这个角为x,则补角为(180°﹣x),余角为(90°﹣x),
由题意得,4(90°﹣x)=180°﹣x,
解得:x=60,即这个角为60°.
故答案为:60°.
15.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,故答案为:42.
16.解:39′+31′=70′=1°10′,
故48°39′+67°31′=116°10'.
故答案为:116°10'.
17.解:(1)若射线OD在OC的下方时,
如图1所示:
∵OC平分∠AOB,
∴∠AOC=,
又∵∠AOB=70°,
∴∠AOC==35°,
又∵∠AOC=∠COD+∠AOD,
∠COD=10°,
∴∠AOD=35°﹣10°=25°;
(2)若射线OD在OC的上方时,
如图2所示:
同(1)可得:∠AOC=35°,
又∵∠AOD=∠AOC+∠COD,
∴∠AOD=35°+10°=45°;
综合所述∠AOD的度数为25°或45°,
故答案为25°或45°.
18.解:(1)射线OC在∠AOB的内部时,
如图1所示:
∵∠AOB=75°,∠AOC=27°,
∠AOB=∠AOC+∠BOC,
∴∠BOC=∠AOB﹣∠AOC=75°﹣27°=48°;
(2)射线OC在∠AOB的外部时,
如图2所示:
∵∠AOB=75°,∠AOC=27°,
∠BOC=∠AOB+∠AOC,
∴∠BOC=75°+27°=102°,
综合所述,∠BOC的度数为48°或102°,
故答案为48°或102°.
19.解:∵OM是∠DOC平分线,ON是∠COB的平分线,
∴∠COM=∠DOM=∠COD,∠BON=∠CON=∠BOC,
∵∠BOC+∠COD=∠BOD=90°,
∴∠COM+∠CON=∠BOD=45°=∠MON,
故答案为:45°
20.解:如图1,当射线OP在∠AOB的内部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOB=∠AOP+∠BOP=5x=17°,
解得:x=3.4°,
则∠AOP=10.2°;
如图2,当射线OP在∠AOB的外部时,设∠AOP=3x,则∠BOP=2x,
∵∠AOP=∠AOB+∠BOP,
又∵∠AOB=17°,
∴3x=17°+2x,
解得:x=17°,
则∠AOP=51°.
故∠AOP的度数为10.2°或51°.
故答案为:10.2°或51°.
21.解:(1)∵∠BOC=40°,
∴∠AOC=140°,
∵OE是∠AOC的角平分线,
∴∠AOE的度数为:140°÷2=70°;
(2)∵OD、OE分别是∠BOC、∠AOC的角平分线,
∴∠AOE=∠EOC,∠COD=∠BOD,
∴∠EOC+∠COD=90°,
∴∠BOD+∠EOC=90°,
∴图中与∠EOC互余的角有∠COD,∠BOD;
(3)∠COE有补角,
理由:∵∠AOE=∠EOC,∠AOE+∠BOE=180°,
∴∠COE+∠BOE=180°,
∴∠COE有补角是∠BOE.
22.解:(1)∠BOC的补角为:∠AOC(或∠BOD、∠AOE)
(2)根据“同角的补角相等”得∠BOD=∠AOC.
∵∠EOD=100°,∠EOD+∠EOC=180°,
∴∠EOC=180°﹣∠EOD=180°﹣100°=80°,
∵OA是∠EOC的平分线,
∴∠AOC=∠EOC=40°.
∴∠BOD=40°.
23.解:(1)如图,∵OB为∠AOC的平分线,OD是∠COE的平分线,
∴∠AOB=∠BOC,∠DOE=∠DOC,
∴∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°;
(2)如图,∵OD是∠COE的平分线,∠COD=30°,
∴∠EOC=2∠COD=60°.
∵∠AOE=140°,∠AOC=∠AOE﹣∠EOC=80°.
又∵OB为∠AOC的平分线,
∴∠AOB=∠AOC=40°.
24.解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+30°=120°,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=×120°=60°,
∠COD=∠BOC=×30°=15°,
∴∠DOE=∠COE﹣∠COD=60°﹣15°=45°;
(2)若∠BOC的度数没有给出,则∠AOC=∠AOB+∠BOC=90°+∠BOC,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=×(90°+∠BOC)=45°+∠BOC,
∠COD=∠BOC,
∴∠DOE=∠COE﹣∠COD=45°+∠BOC﹣∠BOC=45°;
(3)由图可知,∠AOC=∠AOB+∠BOC,
∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠COE=∠AOC=(∠AOB+∠BOC),
∠COD=∠BOC,
∴∠DOE=(∠AOB+∠BOC)﹣∠BOC=∠AOB,
∵∠AOB=α,
∴∠DOE=α.
规律:无论∠BOC的大小如何变化,∠DOE始终为∠AOB的一半.
25.解:(1)(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,=β+∠AOB,=α+β.
26.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°﹣∠AOB=180°﹣120°=60°,
(2)∠DOE与∠AOB互补,理由如下:
∵∠DOC=∠BOC=×70°=35°,∠COE=∠AOC=×50°=25°.
∴∠DOE=∠DOC+∠COE=35°+25°=60°.
∴∠DOE+∠AOB=60°+70°+50°=180°,
∴∠DOE与∠AOB互补.
(3)∠DOE与∠AOB不一定互补,理由如下:
∵∠DOC=∠BOC=α,∠COE=∠AOC=β,
∴∠DOE=∠DOC+∠COE=α+β=(α+β),
∴∠DOE+∠AOB=(α+β)+(α+β)=(α+β),
∵α+β的度数不确定
∴∠DOE与∠AOB不一定互补.
27.解:Ⅰ(1)∵∠MOC=∠AOC﹣∠AOM=150°﹣90°=60°,
∴射线OC表示的方向为北偏东60°;
(2)∵∠BON=2∠NOC,OC平分∠MOB,
∴∠MOC=∠BOC=3∠NOC,
∵∠MOC+∠NOC=∠MON=90°,
∴3∠NOC+∠NOC=90°,
∴4∠NOC=90°,
∴∠BON=2∠NOC=45°,
∴∠AOM=180°﹣∠MON﹣∠BON=180°﹣90°﹣45°=45°;
Ⅱ.如图1:
∵∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=∠AOB=α,∠CON=∠BON=∠COB=β,
∴∠MON=∠BOM+∠CON=,
如图2,
∠MON=∠BOM﹣∠BON=;
如图3,
∠MON=∠BON﹣∠BOM=,
∴∠MON为或或
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
