高中数学人教A版必修5第一章1.1.2 余弦定理(1)课件(共16张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第一章1.1.2 余弦定理(1)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 18:10:13 | ||
图片预览





文档简介
余弦定理
必修5 —1.1.2
复习回顾
正弦定理:
三角形题型:
(1)知三边(SSS);
(2)知两角一边(AAS、ASA);
(3)知两边一角(SSA、SAS)
待解决:(SSS)、(SAS)?
定理用途:
2.解三角形
?
?
?
?
?
1.边角互化
(知三求三解)
请同学们试着改变已知的边和角,不改变边角位置关系,看又能得出什么结果?
解:
C
B
c
a
b
A
﹚
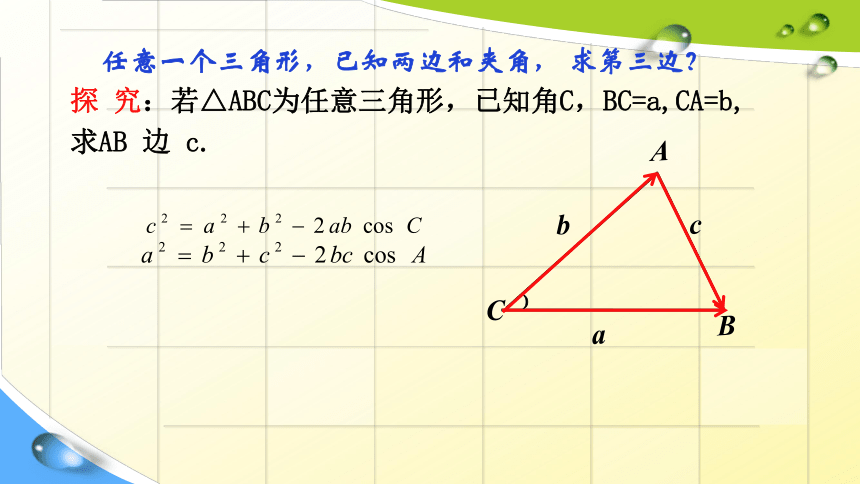
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
C
B
A
c
a
b
﹚
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
C
B
A
c
a
b
﹚
余弦定理
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
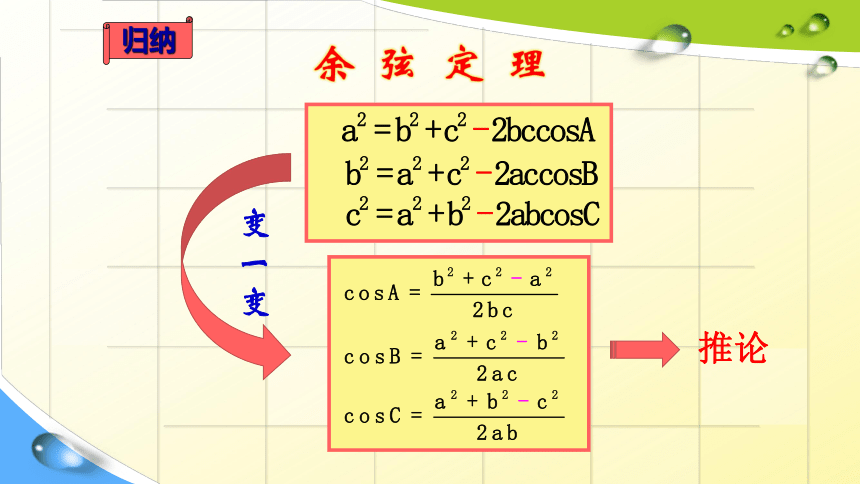
余 弦 定 理
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
文字语言:
C
B
A
a
b
c
归纳
对余弦定理,还有其他证明方法吗?
解析法
几何法
余 弦 定 理
变一变
归纳
推论
剖 析 定 理
问题1:公式有怎样的结构特征?
(1)轮换对称,简洁优美;
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
问题2:余弦定理的用途是什么?
剖 析 定 理
(1)已知三边
求三个角 SSS
问题2:余弦定理在解三角形中的作用是什么?
(2)已知两边和它们的夹角,求第三边和其他两个角. SAS
剖 析 定 理
已知a、b、c(三边),可以求什么?
钝角三角形
直角三角形
锐角三角形
当A为最大角
剖 析 定 理
(3)余弦定理可以判断三角形的形状 。
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
应 用 定 理
例1.在△ABC中,已知a=5,c=4,B=60°,求b。
题型一:已知两边及夹角,求其他边角
解:由余弦定理得
总结1 : 抓住定理的结构特征,记牢公式
例2.在△ABC中,已知a=1,b=2,c= ,求最大角的度数。
由大边对大角知 最大内角为∠C,
题型二:已知三边,求其他角
解:
由余弦定理
应 用 定 理
总结2:
①余弦定理还可以解决:已知两边及其中一边对角,求第三边和其他两个角;
②恰当选用正弦、余弦定理解三角形.
例3. 在△ABC中已知 a= ,b=1,B=30,求 c。
题型三:已知两边和一边对角
有两解
C
B
A
a
b
c
由余弦定理得
代入数值得
整理得
解得
解:
应 用 定 理
1.余弦定理
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
课 堂 小 结
(1)已知三边求三个角;(SSS)
(2)已知两边和它们的夹角,求第三边和其他两个角. (SAS)
2.余弦定理的作用
(3)已知两边和一边对角,
求另外一边和其他两角(SSA)
再见
必修5 —1.1.2
复习回顾
正弦定理:
三角形题型:
(1)知三边(SSS);
(2)知两角一边(AAS、ASA);
(3)知两边一角(SSA、SAS)
待解决:(SSS)、(SAS)?
定理用途:
2.解三角形
?
?
?
?
?
1.边角互化
(知三求三解)
请同学们试着改变已知的边和角,不改变边角位置关系,看又能得出什么结果?
解:
C
B
c
a
b
A
﹚
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
C
B
A
c
a
b
﹚
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
C
B
A
c
a
b
﹚
余弦定理
探 究:若△ABC为任意三角形,已知角C,BC=a,CA=b,
求AB 边 c.
任意一个三角形,已知两边和夹角, 求第三边?
余 弦 定 理
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
文字语言:
C
B
A
a
b
c
归纳
对余弦定理,还有其他证明方法吗?
解析法
几何法
余 弦 定 理
变一变
归纳
推论
剖 析 定 理
问题1:公式有怎样的结构特征?
(1)轮换对称,简洁优美;
(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
问题2:余弦定理的用途是什么?
剖 析 定 理
(1)已知三边
求三个角 SSS
问题2:余弦定理在解三角形中的作用是什么?
(2)已知两边和它们的夹角,求第三边和其他两个角. SAS
剖 析 定 理
已知a、b、c(三边),可以求什么?
钝角三角形
直角三角形
锐角三角形
当A为最大角
剖 析 定 理
(3)余弦定理可以判断三角形的形状 。
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
应 用 定 理
例1.在△ABC中,已知a=5,c=4,B=60°,求b。
题型一:已知两边及夹角,求其他边角
解:由余弦定理得
总结1 : 抓住定理的结构特征,记牢公式
例2.在△ABC中,已知a=1,b=2,c= ,求最大角的度数。
由大边对大角知 最大内角为∠C,
题型二:已知三边,求其他角
解:
由余弦定理
应 用 定 理
总结2:
①余弦定理还可以解决:已知两边及其中一边对角,求第三边和其他两个角;
②恰当选用正弦、余弦定理解三角形.
例3. 在△ABC中已知 a= ,b=1,B=30,求 c。
题型三:已知两边和一边对角
有两解
C
B
A
a
b
c
由余弦定理得
代入数值得
整理得
解得
解:
应 用 定 理
1.余弦定理
a =b +c-2bccosA
b =c +a-2accosB
c =a +b-2abcosC
2
2
2
2
2
2
2
2
2
课 堂 小 结
(1)已知三边求三个角;(SSS)
(2)已知两边和它们的夹角,求第三边和其他两个角. (SAS)
2.余弦定理的作用
(3)已知两边和一边对角,
求另外一边和其他两角(SSA)
再见
