高一数学人教A版必修4第一章1.1.2 弧度制 课件(共24张PPT)
文档属性
| 名称 | 高一数学人教A版必修4第一章1.1.2 弧度制 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览







文档简介
1.1.2 弧度制
1元=100分=10分×10分
=0.1元×0.1元=0.01元=1分
1°=60'
1'=60''
问题1:求证1元=1分
问题2:角度制是几进制?
数学史欣赏:
大数学家欧拉
数学史欣赏:欧拉就在身边
1、创立简化符号:
如sin,cos,f(x),e, Σ,i 等
2、无穷小分析概论:
首次提出弧度制思想
思考1:
1°的角是怎样定义的?
探究1:弧度的概念:
思考2:
1弧度的角是如何定义的?
周角的 叫做1度角,记为1°
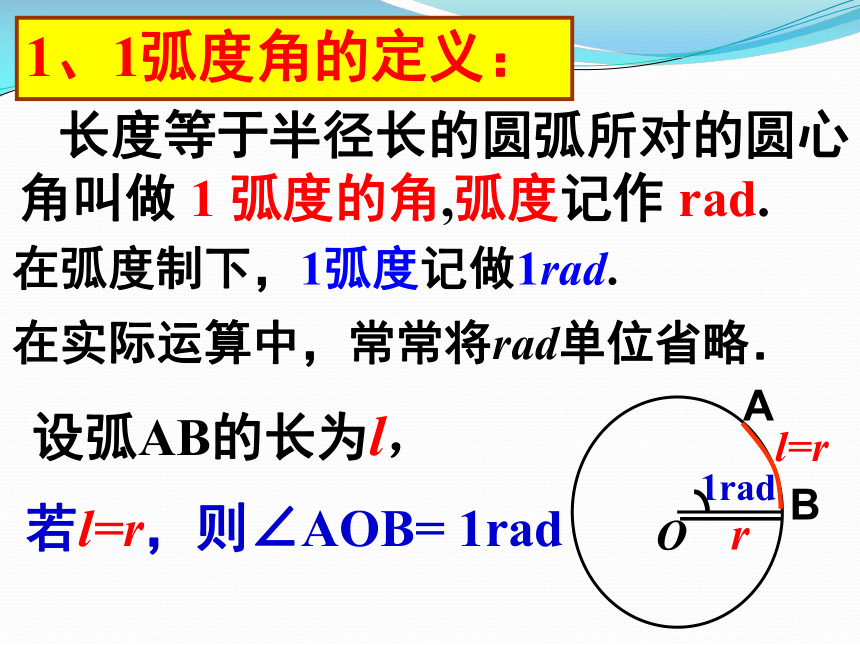
设弧AB的长为l,
若l=r,则∠AOB= 1rad
1、1弧度角的定义:
长度等于半径长的圆弧所对的圆心角叫做 1 弧度的角,弧度记作 rad.
在弧度制下,1弧度记做1rad.
在实际运算中,常常将rad单位省略.
O r
l=r
1rad
A
B
1弧度角的定义:
用弧度做单位来度量角的单位制叫做 弧度制
长度等于半径长的弧所对的圆心角叫做1弧度的角.
记作:1 rad ,读作:1弧度。
2、学生动手做一个1弧度的角
一定大小的圆心角?与半径大小无关。
1rad
r
l=r
O
A
B
设弧AB的长为l,
O
A
B
l=2r
2rad
l=3r
r
3 rad
r
完成导学案探究二
弧AB的长
角AOB的弧度数
OB的旋转方向
?
2?
1
2
弧 AB的长
角AOB的弧度数
OB旋转方向
-2
-2?
-?
0
l=?r
l=2?r
l=2r
l=0
探究二:半径为r的圆的圆心与原点重合,角? 的始边与x轴的非负半轴重合,交圆于点A,终边与圆相交于点B。问题:完成下表。并思考:弧长 、半径 r、和圆心角的弧度数 ? 之间有什么关系?
y
O
x
A
B
顺时针
顺时针
顺时针
不作任何旋转
l=r
l=2r
l=?r
l= 2?r
逆时针
逆时针
逆时针
逆时针
单位弧度rad可以省略,角度不能省略。
弧 AB的长
角AOB的弧度数
OB的旋转方向
?
2?
1
2
弧 AB的长
角AOB的弧度数
OB旋转方向
-2
-2?
-?
0
?r
2?r
2r
0
顺时针
顺时针
顺时针
不作任何旋转
r
2r
?r
2?r
逆时针
逆时针
逆时针
逆时针
思考:弧长 、半径 r、和圆心角的弧度数 ? 之间有什么关系?
实数集R
角的弧度数
正角
零角
负角
正实数
零
负实数
一一对应
对应的弧度数
一般规律:
?的正负由角?的终边的旋转方向决定.
一定大小的圆心角?是由所对应的弧长与半径的比值唯一确定的,与半径大小无关。
2.角?的弧度数的绝对值:
弧度制与角度制都是角的度量单位,那么它们之间是如何换算的?
360°= rad
180°= rad
2π
π
探究三:角度制与弧度制的换算
180°= rad
π
探究三:角度制与弧度制的换算
1°= rad
?
0.01745 rad
1rad=
?
°
根据这两个式子就可以进行弧度与角度的换算.
例1:将下列各角度化成弧度:
1)160° 2)-210° 3)1200°
例2. 将下列各弧度化成角度:
(1) (2) (3)
-240°
54°
角度n?
弧度?
总结:
角
度
0o
30o
45o
60o
90o
120o
弧
度
0
角
度
135o
150o
180o
270o
360o
弧
度
π
2π
例3、特殊角的度数与弧度数对应表:
熟记!
请分别说出1rad,2rad,3rad,4rad,5rad,6rad 终边所在象限.
思考
本节课你收获了什么?
六、作业布置。
习题1.1 A组 第7,8题
1元=100分=10分×10分
=0.1元×0.1元=0.01元=1分
1°=60'
1'=60''
问题1:求证1元=1分
问题2:角度制是几进制?
数学史欣赏:
大数学家欧拉
数学史欣赏:欧拉就在身边
1、创立简化符号:
如sin,cos,f(x),e, Σ,i 等
2、无穷小分析概论:
首次提出弧度制思想
思考1:
1°的角是怎样定义的?
探究1:弧度的概念:
思考2:
1弧度的角是如何定义的?
周角的 叫做1度角,记为1°
设弧AB的长为l,
若l=r,则∠AOB= 1rad
1、1弧度角的定义:
长度等于半径长的圆弧所对的圆心角叫做 1 弧度的角,弧度记作 rad.
在弧度制下,1弧度记做1rad.
在实际运算中,常常将rad单位省略.
O r
l=r
1rad
A
B
1弧度角的定义:
用弧度做单位来度量角的单位制叫做 弧度制
长度等于半径长的弧所对的圆心角叫做1弧度的角.
记作:1 rad ,读作:1弧度。
2、学生动手做一个1弧度的角
一定大小的圆心角?与半径大小无关。
1rad
r
l=r
O
A
B
设弧AB的长为l,
O
A
B
l=2r
2rad
l=3r
r
3 rad
r
完成导学案探究二
弧AB的长
角AOB的弧度数
OB的旋转方向
?
2?
1
2
弧 AB的长
角AOB的弧度数
OB旋转方向
-2
-2?
-?
0
l=?r
l=2?r
l=2r
l=0
探究二:半径为r的圆的圆心与原点重合,角? 的始边与x轴的非负半轴重合,交圆于点A,终边与圆相交于点B。问题:完成下表。并思考:弧长 、半径 r、和圆心角的弧度数 ? 之间有什么关系?
y
O
x
A
B
顺时针
顺时针
顺时针
不作任何旋转
l=r
l=2r
l=?r
l= 2?r
逆时针
逆时针
逆时针
逆时针
单位弧度rad可以省略,角度不能省略。
弧 AB的长
角AOB的弧度数
OB的旋转方向
?
2?
1
2
弧 AB的长
角AOB的弧度数
OB旋转方向
-2
-2?
-?
0
?r
2?r
2r
0
顺时针
顺时针
顺时针
不作任何旋转
r
2r
?r
2?r
逆时针
逆时针
逆时针
逆时针
思考:弧长 、半径 r、和圆心角的弧度数 ? 之间有什么关系?
实数集R
角的弧度数
正角
零角
负角
正实数
零
负实数
一一对应
对应的弧度数
一般规律:
?的正负由角?的终边的旋转方向决定.
一定大小的圆心角?是由所对应的弧长与半径的比值唯一确定的,与半径大小无关。
2.角?的弧度数的绝对值:
弧度制与角度制都是角的度量单位,那么它们之间是如何换算的?
360°= rad
180°= rad
2π
π
探究三:角度制与弧度制的换算
180°= rad
π
探究三:角度制与弧度制的换算
1°= rad
?
0.01745 rad
1rad=
?
°
根据这两个式子就可以进行弧度与角度的换算.
例1:将下列各角度化成弧度:
1)160° 2)-210° 3)1200°
例2. 将下列各弧度化成角度:
(1) (2) (3)
-240°
54°
角度n?
弧度?
总结:
角
度
0o
30o
45o
60o
90o
120o
弧
度
0
角
度
135o
150o
180o
270o
360o
弧
度
π
2π
例3、特殊角的度数与弧度数对应表:
熟记!
请分别说出1rad,2rad,3rad,4rad,5rad,6rad 终边所在象限.
思考
本节课你收获了什么?
六、作业布置。
习题1.1 A组 第7,8题
