1.2.4单位圆的对称性与诱导公式 课件-北师大版数学必修四(23张PPT)
文档属性
| 名称 | 1.2.4单位圆的对称性与诱导公式 课件-北师大版数学必修四(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览








文档简介
§1.4.4单位圆的对称性与诱导公式课件
教学目标
1.了解特殊角的终边的对称关系.
2.能借助单位圆直观地探索正弦函数、余弦函数的诱导公式.
3.会利用诱导公式求任意角的正弦函数、余弦函数.
教学重、难点
重点:正弦函数、余弦函数的诱导公式的应用.
难点:正弦函数、余弦函数的诱导公式的探索及熟记.
预习课本,完成下列问题:
1、如何利用单位圆推导诱导公式?
2、如何寻找角的终边的对称关系?
3、如何识记诱导公式?
知识点一 正弦函数和余弦函数的诱导公式
新知初探
sinα
cosα
-sinα
cosα
-sinα
cosα
sinα
-cosα
-sinα
-cosα
cosα
-sinα
cosα
sinα
知识点二 诱导公式的记忆方法
新知初探
(1)“变”与“不变”是指互余的两个角的三角函数名改变.
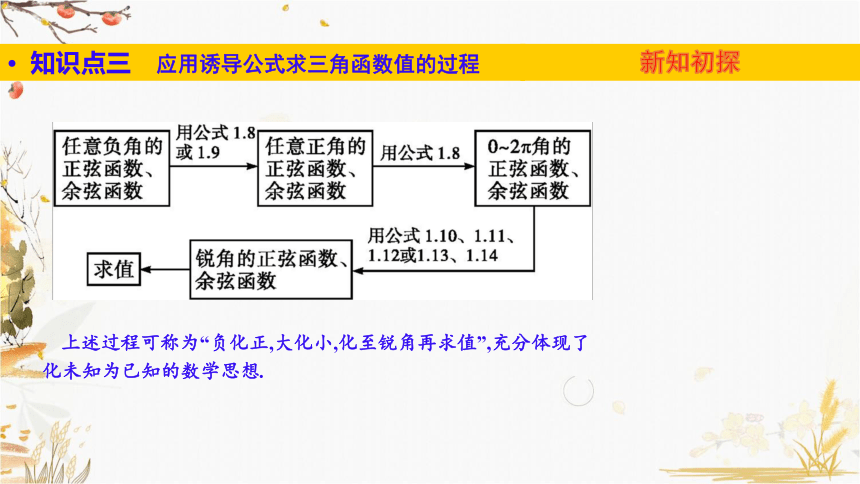
知识点三 应用诱导公式求三角函数值的过程
新知初探
上述过程可称为“负化正,大化小,化至锐角再求值”,充分体现了化未知为已知的数学思想.
【基础检测】
1、判一判(正确的打“√”,错误的打“×”)
(1)终边相同的角的同一个三角函数值相等.( )
(2)若角α与角β的终边关于x轴对称,必有β=-α成立.( )
(3)已知A,B,C是三角形ABC的三个内角,则sin(A+B)=sinC.( )
答案:(1)√ (2)× (3)√
2.做一做(请把正确的答案写在横线上)
(1)sin390°的值是_______.
(2) 的值是_______.
(3)在△ABC中, =________.
【解析】
(1)sin 390°=sin(360°+30°)=sin(30°)=sin 30°=
(2)
(3)在△ABC中,因为
所以
3、sin 105°+cos 165°的值为( )
A.sin 5° B.cos 5° C.0 D.2sin 5°
答案:C
4、求值: (n∈Z)
解析:
解析 ∵sin(2π-α)=-sin α=-0.3,
∴sin α=0.3, ∴sin(π+α)=-sin α=-0.3.
5、已知sin(2π-α)=-0.3,则sin(π+α)= .
6.若 则f(cosx)=_______.
【解析】因为f(sinx)= =sin x,
所以f(cos x)=cosx.
答案:cosx
利用秀导公式求三角函数值
例1、求值:cos(-1440°)+sin390°=________.
【解析】原式=cos1440°+sin390°
=cos(4×360°+0°)+sin(360°+30°)=cos0°+sin 30°=
答案:
利用诱导公式化简
例2、化简: =_______.
【解析】原式=
答案:-sinα
利用诱导公式证明三角恒等式
例3、已知A,B,C为△ABC的三个内角,求证:cos(2A+B+C)=cos( π-A).
证明:因为A,B,C为△ABC的三个内角,所以A+B+C=π.
左边=cos(2A+B+C)=cos(A+A+B+C)=cos(π+A)=-cos A.
右边=cos( π-A)=-cos A.所以元不等式成立
1.当α∈R时,下列各式中恒成立的是( )
C.cos(π-α)=cos α D.cos(2π-α)=cos α
答案:D
3、已知函数f(x)满足f(cosx)=cos2x,则f(sin75°)=______.
【解析】f(sin75°)=f(cos15°)=cos30°=
4、若 则 =__________.
【解析】因为
所以
所以
5、已知α为第三象限角,f(α)=
①化简f(α);
②若 求f(α)的值.
(2)①f(α)=
=
②因为
=cosα,所以 即
布置作业
化简下列各式.
(1)
(2)
课
堂
小
结
堂
小
结
求已知角的函数值问题,主要是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解.如果是负角,一般先将负角的三角函数化为正角的三角函数,同时,要准确记忆特殊角的三角函数值.
教学目标
1.了解特殊角的终边的对称关系.
2.能借助单位圆直观地探索正弦函数、余弦函数的诱导公式.
3.会利用诱导公式求任意角的正弦函数、余弦函数.
教学重、难点
重点:正弦函数、余弦函数的诱导公式的应用.
难点:正弦函数、余弦函数的诱导公式的探索及熟记.
预习课本,完成下列问题:
1、如何利用单位圆推导诱导公式?
2、如何寻找角的终边的对称关系?
3、如何识记诱导公式?
知识点一 正弦函数和余弦函数的诱导公式
新知初探
sinα
cosα
-sinα
cosα
-sinα
cosα
sinα
-cosα
-sinα
-cosα
cosα
-sinα
cosα
sinα
知识点二 诱导公式的记忆方法
新知初探
(1)“变”与“不变”是指互余的两个角的三角函数名改变.
知识点三 应用诱导公式求三角函数值的过程
新知初探
上述过程可称为“负化正,大化小,化至锐角再求值”,充分体现了化未知为已知的数学思想.
【基础检测】
1、判一判(正确的打“√”,错误的打“×”)
(1)终边相同的角的同一个三角函数值相等.( )
(2)若角α与角β的终边关于x轴对称,必有β=-α成立.( )
(3)已知A,B,C是三角形ABC的三个内角,则sin(A+B)=sinC.( )
答案:(1)√ (2)× (3)√
2.做一做(请把正确的答案写在横线上)
(1)sin390°的值是_______.
(2) 的值是_______.
(3)在△ABC中, =________.
【解析】
(1)sin 390°=sin(360°+30°)=sin(30°)=sin 30°=
(2)
(3)在△ABC中,因为
所以
3、sin 105°+cos 165°的值为( )
A.sin 5° B.cos 5° C.0 D.2sin 5°
答案:C
4、求值: (n∈Z)
解析:
解析 ∵sin(2π-α)=-sin α=-0.3,
∴sin α=0.3, ∴sin(π+α)=-sin α=-0.3.
5、已知sin(2π-α)=-0.3,则sin(π+α)= .
6.若 则f(cosx)=_______.
【解析】因为f(sinx)= =sin x,
所以f(cos x)=cosx.
答案:cosx
利用秀导公式求三角函数值
例1、求值:cos(-1440°)+sin390°=________.
【解析】原式=cos1440°+sin390°
=cos(4×360°+0°)+sin(360°+30°)=cos0°+sin 30°=
答案:
利用诱导公式化简
例2、化简: =_______.
【解析】原式=
答案:-sinα
利用诱导公式证明三角恒等式
例3、已知A,B,C为△ABC的三个内角,求证:cos(2A+B+C)=cos( π-A).
证明:因为A,B,C为△ABC的三个内角,所以A+B+C=π.
左边=cos(2A+B+C)=cos(A+A+B+C)=cos(π+A)=-cos A.
右边=cos( π-A)=-cos A.所以元不等式成立
1.当α∈R时,下列各式中恒成立的是( )
C.cos(π-α)=cos α D.cos(2π-α)=cos α
答案:D
3、已知函数f(x)满足f(cosx)=cos2x,则f(sin75°)=______.
【解析】f(sin75°)=f(cos15°)=cos30°=
4、若 则 =__________.
【解析】因为
所以
所以
5、已知α为第三象限角,f(α)=
①化简f(α);
②若 求f(α)的值.
(2)①f(α)=
=
②因为
=cosα,所以 即
布置作业
化简下列各式.
(1)
(2)
课
堂
小
结
堂
小
结
求已知角的函数值问题,主要是利用诱导公式把任意角的三角函数值转化为锐角的三角函数值求解.如果是负角,一般先将负角的三角函数化为正角的三角函数,同时,要准确记忆特殊角的三角函数值.
