2020--2021学年北师大版九年级数学下册第三章 圆专题训练(五)(Word版 含解析)
文档属性
| 名称 | 2020--2021学年北师大版九年级数学下册第三章 圆专题训练(五)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览



文档简介
九年级数学下册第三章 圆 压轴题
过关强化专题训练(五)
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
2.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC,垂足为M,AB、MD的延长线交于点N.
(1)求证:MN是⊙O的切线;
(2)求证:DN2=BN?(BN+AC);
(3)若BC=6,cosC=,求DN的长.
3.如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点“,把PQ?PH的值称为⊙I关于直线a的“特征数”.
(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4).半径为1的⊙O与两坐标轴交于点A、B、C、D.
①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点 (填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为 ;
②若直线n的函数表达式为y=x+4.求⊙O关于直线n的“特征数”;
(2)在平面直角坐标系xOy中,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线l相离,点N(﹣1,0)是⊙F关于直线l的“远点”.且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.
4.如图,在△ACE中,以AC为直径的⊙O交CE于点D,连接AD,且∠DAE=∠ACE,连接OD并延长交AE的延长线于点P,PB与⊙O相切于点B.
(1)求证:AP是⊙O的切线;
(2)连接AB交OP于点F,求证:△FAD∽△DAE;
(3)若tan∠OAF=,求的值.
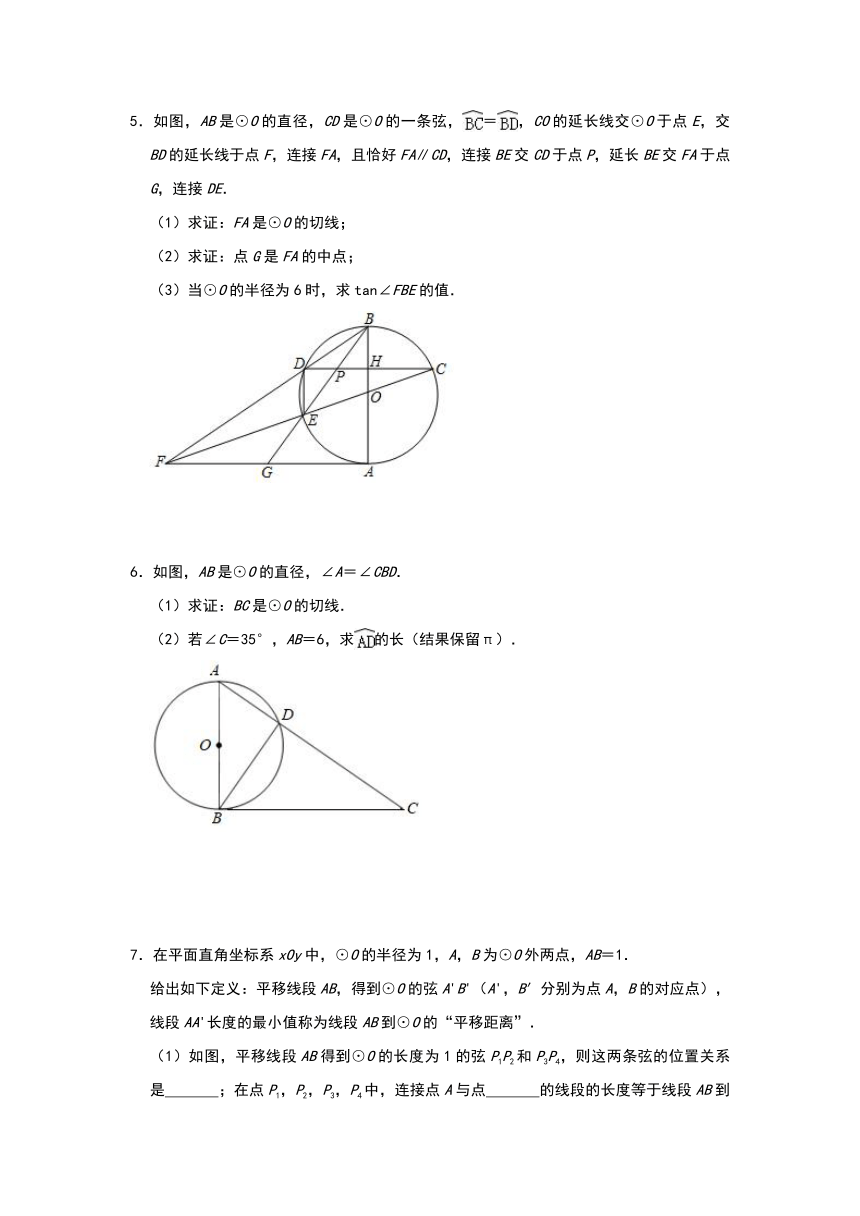
5.如图,AB是⊙O的直径,CD是⊙O的一条弦,=,CO的延长线交⊙O于点E,交BD的延长线于点F,连接FA,且恰好FA∥CD,连接BE交CD于点P,延长BE交FA于点G,连接DE.
(1)求证:FA是⊙O的切线;
(2)求证:点G是FA的中点;
(3)当⊙O的半径为6时,求tan∠FBE的值.
6.如图,AB是⊙O的直径,∠A=∠CBD.
(1)求证:BC是⊙O的切线.
(2)若∠C=35°,AB=6,求的长(结果保留π).
7.在平面直角坐标系xOy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.
给出如下定义:平移线段AB,得到⊙O的弦A'B'(A',B′分别为点A,B的对应点),线段AA'长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB得到⊙O的长度为1的弦P1P2和P3P4,则这两条弦的位置关系是 ;在点P1,P2,P3,P4中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线y=x+2上,记线段AB到⊙O的“平移距离”为d1,求d1的最小值;
(3)若点A的坐标为(2,),记线段AB到⊙O的“平移距离”为d2,直接写出d2的取值范围.
8.如图,在⊙O中,∠ABC=45°,CE是⊙O的切线,BO的延长线交⊙O于点D,交切线CE于点E,OA与CD的延长线交于点F.
(1)求证:OF∥EC.
(2)若DF=6,tan∠EBC=,求AF的值.
9.如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AC与BD交于点E,P为CB延长线上一点,连接PA,且∠PAB=∠ADB.
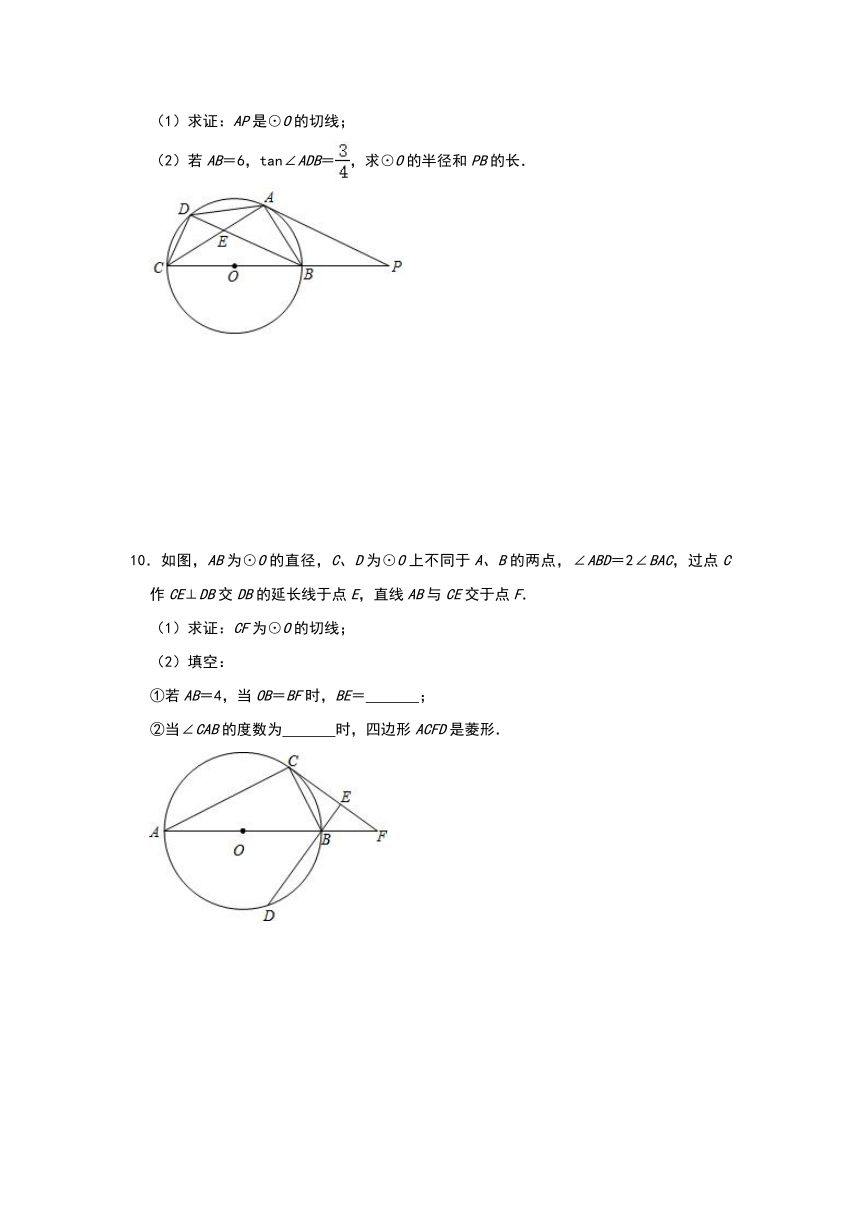
(1)求证:AP是⊙O的切线;
(2)若AB=6,tan∠ADB=,求⊙O的半径和PB的长.
10.如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:
①若AB=4,当OB=BF时,BE= ;
②当∠CAB的度数为 时,四边形ACFD是菱形.
参考答案
1.解:(1)EF与⊙O相切,理由如下:
连接AD,OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
∵EF⊥AC,
∴EF⊥OD.
∴EF与⊙O相切.
(2)解:由(1)知∠ADC=90°,AC=AB=10,
在Rt△ADC中,由勾股定理得:AD===8.
∵SACD=AD?CD=AC?DE,
∴×8×6=×10×DE.
∴DE=.
(3)证明:由(1)得:CD=BC,AD⊥BC,
∴∠ADC=90°,
∵EF⊥AC,
∴∠DEC=90°=∠ADC,
∵∠C=∠C,
∴△CDE∽△CAD,
∴=,
∴CD2=CE?AB,
∵AB=AC,
∴BC2=CE?AB,
∴BC2=4CE?AB.
2.证明:(1)如图,连接OD,
∵AB是直径,
∴∠ADB=90°,
又∵AB=AC,
∴BD=CD,∠BAD=∠CAD,
∵AO=BO,BD=CD,
∴OD∥AC,
∵DM⊥AC,
∴OD⊥MN,
又∵OD是半径,
∴MN是⊙O的切线;
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC+∠BAD=90°,∠ACB+∠CDM=90°,
∴∠BAD=∠CDM,
∵∠BDN=∠CDM,
∴∠BAD=∠BDN,
又∵∠N=∠N,
∴△BDN∽△DAN,
∴,
∴DN2=BN?AN=BN?(BN+AB)=BN?(BN+AC);
(3)∵BC=6,BD=CD,
∴BD=CD=3,
∵cosC==,
∴AC=5,
∴AB=5,
∴AD===4,
∵△BDN∽△DAN,
∴==,
∴BN=DN,DN=AN,
∴BN=(AN)=AN,
∵BN+AB=AN,
∴AN+5=AN
∴AN=,
∴DN=AN=.
3.解:(1)①由题意,点D是⊙O关于直线m的“远点”,⊙O关于直线m的特征数=DB?DE=2×5=10,
故答案为:D,10.
②如图1中,过点O作OH⊥直线n于H,交⊙O于Q,P.
设直线y=x+4交x轴于F(﹣,0),交y轴于E(0,4),
∴OE=4,OF=,
∴tan∠FEO==,
∴∠FEO=30°,
∴OH=OE=2,
∴PH=OH+OP=3,
∴⊙O关于直线n的“特征数”=PQ?PH=2×3=6.
(2)如图2中,设直线l的解析式为y=kx+b.
当k>0时,过点F作FH⊥直线l于H,交⊙F于E,N.
由题意,EN=2,EN?NH=4,
∴NH=,
∵N(﹣1,0),M(1,4),
∴MN==2,
∴HM===,
∴△MNH是等腰直角三角形,
∵MN的中点K(0,2),
∴KN=HK=KM=,
∴H(﹣2,3),
把H(﹣2,3),M(1,4)代入y=kx+b,则有,
解得,
∴直线l的解析式为y=x+,
当k<0时,同法可知直线l′经过H′(2,1),可得直线l′的解析式为y=﹣3x+7.
综上所述,满足条件的直线l的解析式为y=x+或y=﹣3x+7.
4.解:(1)∵AC为直径,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠DAE=∠ACE,
∴∠DAC+∠DAE=90°,
即∠CAE=90°,
∴AP是⊙O的切线;
(2)连接DB,如图1,
∵PA和PB都是切线,
∴PA=PB,∠OPA=∠OPB,PO⊥AB,
∵PD=PD,
∴△DPA≌△DPB(SAS),
∴AD=BD,
∴∠ABD=∠BAD,
∵∠ACD=∠ABD,
又∠DAE=∠ACE,
∴∠DAF=∠DAE,
∵AC是直径,
∴∠ADE=∠ADC=90°,
∴∠ADE=∠AFD=90°,
∴△FAD∽△DAE;
(3)∵∠AFO=∠OAP=90°,∠AOF=∠POA,
∴△AOF∽△POA,
∴,
∴,
∴PA=2AO=AC,
∵∠AFD=∠CAE=90°,∠DAF=∠ABD=∠ACE,
∴△AFD∽△CAE,
∴,
∴,
∵,
不妨设OF=x,则AF=2x,
∴,
∴,
∴,
∴.
5.(1)证明:∵AB是⊙O的直径,CD是⊙O的一条弦,=,
∴AB⊥CD,
又∵FA∥CD,
∴FA⊥AB,
∵OA过O,
∴FA是⊙O的切线;
(2)证明:连接AE,
∵AB是⊙O的直径,
∴AE⊥BG,
又∵FA⊥AB,
∴∠GEA=∠BAG,
又∵∠BGA=∠EGA,
∴△GAB∽△GEA,
∴=,
∴GA2=GB×EG,
∵FA∥CD,
∴∠C=∠EFG,
又∵∠C=∠FBE,
∴∠EFG=∠FBE,
又∵∠FGE=∠BGF,
∴△FEG∽△BFG,
∴=,
∴GF2=GB×GE,
∴GF=GA,
∴G为AF的中点;
(3)解:∵FA∥CD,
∴==,
又∵GF=GA,
∴DP=HP,
又∵CE是⊙O的直径,D在圆上,
∴CD⊥DE,
又∵AB⊥CD于点H,EO=OC,
∴点H是CD的中点,AB∥DE,
又∵DP=HP,
∴DE=BH,
又∵点O是CE中点,点H是CD的中点,
∴OH=DE=BH,
又∵⊙O的半径为6,
∴OH=2,CH===4,
∴tan∠FBE=tanC===.
6.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠A=∠CBD,
∴∠CBD+∠ABD=90°,即∠ABC=90°,
∴BC⊥AB,
∴BC是⊙O的切线.
(2)解:连接OD,如图所示:
∵∠ABC=90°,
∴∠C+∠A=90°,
又∠A+∠ABD=90°,
∴∠ABD=∠C=35°,
∴∠AOD=2∠ABD=70°,
∵直径AB=6,
∴OA=3,
∴的长==.
7.解:(1)如图,平移线段AB得到⊙O的长度为1的弦P1P2和P3P4,则这两条弦的位置关系是P1P2∥P3P4;在点P1,P2,P3,P4中,连接点A与点P3的线段的长度等于线段AB到⊙O的“平移距离”.
故答案为:P1P2∥P3P4,P3.
(2)如图1中,作等边△OEF,点E在x轴上,OE=EF=OF=1,
设直线y=x+2交x轴于M,交y轴于N.则M(﹣2,0),N(0,2),
过点E作EH⊥MN于H,
∵OM=2,ON=2,
∴tan∠NMO=,
∴∠NMO=60°,
∴EH=EM?sin60°=,
观察图象可知,线段AB到⊙O的“平移距离”为d1的最小值为.
(3)如图2中,以A为圆心1为半径作⊙A,作直线OA交⊙O于M,交⊙A于N,
以OA,AB为邻边构造平行四边形ABDO,以OD为边构造等边△ODB′,等边△OB′A′,则AB∥A′B′,AA′的长即为线段AB到⊙O的“平移距离”,
当点A′与M重合时,AA′的值最小,最小值=OA﹣OM=﹣1=,
当点B与N重合时,AA′的长最大,如图3中,过点A′作A′H⊥OA于H.
由题意A′H=,AH=+=3,
∴AA′的最大值==,
∴≤d2≤.
8.解:(1)∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴∠OCD+∠F=90°,
∵CE是⊙O的切线,
∴∠OCE=90°,
∴∠OCD+∠DCE=90°,
∴∠F=∠DCE,
∴OF∥CE;
(2)∵OC=OD,
∴∠OCD=∠ODC,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠EBC+∠ODC=90°,
∵∠F+∠OCD=90°,
∴∠F=∠EBC,
∴tan∠F==tan∠EBC==,
设CD=x,则BC=2x,
∴BD=x,
∴OC=OB=x,
∴OF=2OC=x,
在Rt△OCF中,OC2+OF2=CF2,
∴,
解得x=4或x=﹣(舍去),
∴CD=4,
∴OF=4,OA=2,
∴AF=OF﹣OA=2.
9.(1)证明:连接OA,
∵OA=OB,
∴∠OAB=∠OBA,
∵BC为⊙O的直径,
∴∠CAB=90°,
∴∠ACB+∠ABC=90°,
∵∠ADB=∠ACB=∠PAB,
∴∠PAB+∠OAB=90°,
∴∠OAP=90°,
∴AP为⊙O的切线;
(2)解:∵∠ADB=∠ACB,
∴tan∠ADB=tan∠ACB=,
∵AB=6,
∴AC=8,
∴BC==10,
∴OB=5,
过B作BF⊥AP于F,
∵∠ADB=∠BAF,
∴tan∠ADB=tan∠BAF=,
∴设AF=4k,BF=3k,
∴AB=5k=6,
∴k=,
∴BF=,
∵OA⊥AP,BF⊥AP,
∴BF∥OA,
∴△PBF∽△POA,
∴,
∴,
∴PB=.
10.证明:(1)连结OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BOC=∠A+∠OCA=2∠OAC,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)①∵AB=4,
∴OB=BF=OC=2,
∴OF=4,
∵BE∥OC,
∴,
∴BE=1,
故答案为:1;
②当∠CAB的度数为30°时,四边形ACFD是菱形,
理由:∵∠CAB=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠CAB=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
,
∴△ACB≌△ADB(AAS),
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形.
故答案为:30°.
过关强化专题训练(五)
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB延长线于点F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若⊙O半径为5,CD=6,求DE的长;
(3)求证:BC2=4CE?AB.
2.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC,垂足为M,AB、MD的延长线交于点N.
(1)求证:MN是⊙O的切线;
(2)求证:DN2=BN?(BN+AC);
(3)若BC=6,cosC=,求DN的长.
3.如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点“,把PQ?PH的值称为⊙I关于直线a的“特征数”.
(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4).半径为1的⊙O与两坐标轴交于点A、B、C、D.
①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点 (填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为 ;
②若直线n的函数表达式为y=x+4.求⊙O关于直线n的“特征数”;
(2)在平面直角坐标系xOy中,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线l相离,点N(﹣1,0)是⊙F关于直线l的“远点”.且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.
4.如图,在△ACE中,以AC为直径的⊙O交CE于点D,连接AD,且∠DAE=∠ACE,连接OD并延长交AE的延长线于点P,PB与⊙O相切于点B.
(1)求证:AP是⊙O的切线;
(2)连接AB交OP于点F,求证:△FAD∽△DAE;
(3)若tan∠OAF=,求的值.
5.如图,AB是⊙O的直径,CD是⊙O的一条弦,=,CO的延长线交⊙O于点E,交BD的延长线于点F,连接FA,且恰好FA∥CD,连接BE交CD于点P,延长BE交FA于点G,连接DE.
(1)求证:FA是⊙O的切线;
(2)求证:点G是FA的中点;
(3)当⊙O的半径为6时,求tan∠FBE的值.
6.如图,AB是⊙O的直径,∠A=∠CBD.
(1)求证:BC是⊙O的切线.
(2)若∠C=35°,AB=6,求的长(结果保留π).
7.在平面直角坐标系xOy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.
给出如下定义:平移线段AB,得到⊙O的弦A'B'(A',B′分别为点A,B的对应点),线段AA'长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB得到⊙O的长度为1的弦P1P2和P3P4,则这两条弦的位置关系是 ;在点P1,P2,P3,P4中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线y=x+2上,记线段AB到⊙O的“平移距离”为d1,求d1的最小值;
(3)若点A的坐标为(2,),记线段AB到⊙O的“平移距离”为d2,直接写出d2的取值范围.
8.如图,在⊙O中,∠ABC=45°,CE是⊙O的切线,BO的延长线交⊙O于点D,交切线CE于点E,OA与CD的延长线交于点F.
(1)求证:OF∥EC.
(2)若DF=6,tan∠EBC=,求AF的值.
9.如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AC与BD交于点E,P为CB延长线上一点,连接PA,且∠PAB=∠ADB.
(1)求证:AP是⊙O的切线;
(2)若AB=6,tan∠ADB=,求⊙O的半径和PB的长.
10.如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:
①若AB=4,当OB=BF时,BE= ;
②当∠CAB的度数为 时,四边形ACFD是菱形.
参考答案
1.解:(1)EF与⊙O相切,理由如下:
连接AD,OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=BC.
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
∵EF⊥AC,
∴EF⊥OD.
∴EF与⊙O相切.
(2)解:由(1)知∠ADC=90°,AC=AB=10,
在Rt△ADC中,由勾股定理得:AD===8.
∵SACD=AD?CD=AC?DE,
∴×8×6=×10×DE.
∴DE=.
(3)证明:由(1)得:CD=BC,AD⊥BC,
∴∠ADC=90°,
∵EF⊥AC,
∴∠DEC=90°=∠ADC,
∵∠C=∠C,
∴△CDE∽△CAD,
∴=,
∴CD2=CE?AB,
∵AB=AC,
∴BC2=CE?AB,
∴BC2=4CE?AB.
2.证明:(1)如图,连接OD,
∵AB是直径,
∴∠ADB=90°,
又∵AB=AC,
∴BD=CD,∠BAD=∠CAD,
∵AO=BO,BD=CD,
∴OD∥AC,
∵DM⊥AC,
∴OD⊥MN,
又∵OD是半径,
∴MN是⊙O的切线;
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC+∠BAD=90°,∠ACB+∠CDM=90°,
∴∠BAD=∠CDM,
∵∠BDN=∠CDM,
∴∠BAD=∠BDN,
又∵∠N=∠N,
∴△BDN∽△DAN,
∴,
∴DN2=BN?AN=BN?(BN+AB)=BN?(BN+AC);
(3)∵BC=6,BD=CD,
∴BD=CD=3,
∵cosC==,
∴AC=5,
∴AB=5,
∴AD===4,
∵△BDN∽△DAN,
∴==,
∴BN=DN,DN=AN,
∴BN=(AN)=AN,
∵BN+AB=AN,
∴AN+5=AN
∴AN=,
∴DN=AN=.
3.解:(1)①由题意,点D是⊙O关于直线m的“远点”,⊙O关于直线m的特征数=DB?DE=2×5=10,
故答案为:D,10.
②如图1中,过点O作OH⊥直线n于H,交⊙O于Q,P.
设直线y=x+4交x轴于F(﹣,0),交y轴于E(0,4),
∴OE=4,OF=,
∴tan∠FEO==,
∴∠FEO=30°,
∴OH=OE=2,
∴PH=OH+OP=3,
∴⊙O关于直线n的“特征数”=PQ?PH=2×3=6.
(2)如图2中,设直线l的解析式为y=kx+b.
当k>0时,过点F作FH⊥直线l于H,交⊙F于E,N.
由题意,EN=2,EN?NH=4,
∴NH=,
∵N(﹣1,0),M(1,4),
∴MN==2,
∴HM===,
∴△MNH是等腰直角三角形,
∵MN的中点K(0,2),
∴KN=HK=KM=,
∴H(﹣2,3),
把H(﹣2,3),M(1,4)代入y=kx+b,则有,
解得,
∴直线l的解析式为y=x+,
当k<0时,同法可知直线l′经过H′(2,1),可得直线l′的解析式为y=﹣3x+7.
综上所述,满足条件的直线l的解析式为y=x+或y=﹣3x+7.
4.解:(1)∵AC为直径,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠DAE=∠ACE,
∴∠DAC+∠DAE=90°,
即∠CAE=90°,
∴AP是⊙O的切线;
(2)连接DB,如图1,
∵PA和PB都是切线,
∴PA=PB,∠OPA=∠OPB,PO⊥AB,
∵PD=PD,
∴△DPA≌△DPB(SAS),
∴AD=BD,
∴∠ABD=∠BAD,
∵∠ACD=∠ABD,
又∠DAE=∠ACE,
∴∠DAF=∠DAE,
∵AC是直径,
∴∠ADE=∠ADC=90°,
∴∠ADE=∠AFD=90°,
∴△FAD∽△DAE;
(3)∵∠AFO=∠OAP=90°,∠AOF=∠POA,
∴△AOF∽△POA,
∴,
∴,
∴PA=2AO=AC,
∵∠AFD=∠CAE=90°,∠DAF=∠ABD=∠ACE,
∴△AFD∽△CAE,
∴,
∴,
∵,
不妨设OF=x,则AF=2x,
∴,
∴,
∴,
∴.
5.(1)证明:∵AB是⊙O的直径,CD是⊙O的一条弦,=,
∴AB⊥CD,
又∵FA∥CD,
∴FA⊥AB,
∵OA过O,
∴FA是⊙O的切线;
(2)证明:连接AE,
∵AB是⊙O的直径,
∴AE⊥BG,
又∵FA⊥AB,
∴∠GEA=∠BAG,
又∵∠BGA=∠EGA,
∴△GAB∽△GEA,
∴=,
∴GA2=GB×EG,
∵FA∥CD,
∴∠C=∠EFG,
又∵∠C=∠FBE,
∴∠EFG=∠FBE,
又∵∠FGE=∠BGF,
∴△FEG∽△BFG,
∴=,
∴GF2=GB×GE,
∴GF=GA,
∴G为AF的中点;
(3)解:∵FA∥CD,
∴==,
又∵GF=GA,
∴DP=HP,
又∵CE是⊙O的直径,D在圆上,
∴CD⊥DE,
又∵AB⊥CD于点H,EO=OC,
∴点H是CD的中点,AB∥DE,
又∵DP=HP,
∴DE=BH,
又∵点O是CE中点,点H是CD的中点,
∴OH=DE=BH,
又∵⊙O的半径为6,
∴OH=2,CH===4,
∴tan∠FBE=tanC===.
6.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠A=∠CBD,
∴∠CBD+∠ABD=90°,即∠ABC=90°,
∴BC⊥AB,
∴BC是⊙O的切线.
(2)解:连接OD,如图所示:
∵∠ABC=90°,
∴∠C+∠A=90°,
又∠A+∠ABD=90°,
∴∠ABD=∠C=35°,
∴∠AOD=2∠ABD=70°,
∵直径AB=6,
∴OA=3,
∴的长==.
7.解:(1)如图,平移线段AB得到⊙O的长度为1的弦P1P2和P3P4,则这两条弦的位置关系是P1P2∥P3P4;在点P1,P2,P3,P4中,连接点A与点P3的线段的长度等于线段AB到⊙O的“平移距离”.
故答案为:P1P2∥P3P4,P3.
(2)如图1中,作等边△OEF,点E在x轴上,OE=EF=OF=1,
设直线y=x+2交x轴于M,交y轴于N.则M(﹣2,0),N(0,2),
过点E作EH⊥MN于H,
∵OM=2,ON=2,
∴tan∠NMO=,
∴∠NMO=60°,
∴EH=EM?sin60°=,
观察图象可知,线段AB到⊙O的“平移距离”为d1的最小值为.
(3)如图2中,以A为圆心1为半径作⊙A,作直线OA交⊙O于M,交⊙A于N,
以OA,AB为邻边构造平行四边形ABDO,以OD为边构造等边△ODB′,等边△OB′A′,则AB∥A′B′,AA′的长即为线段AB到⊙O的“平移距离”,
当点A′与M重合时,AA′的值最小,最小值=OA﹣OM=﹣1=,
当点B与N重合时,AA′的长最大,如图3中,过点A′作A′H⊥OA于H.
由题意A′H=,AH=+=3,
∴AA′的最大值==,
∴≤d2≤.
8.解:(1)∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴∠OCD+∠F=90°,
∵CE是⊙O的切线,
∴∠OCE=90°,
∴∠OCD+∠DCE=90°,
∴∠F=∠DCE,
∴OF∥CE;
(2)∵OC=OD,
∴∠OCD=∠ODC,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠EBC+∠ODC=90°,
∵∠F+∠OCD=90°,
∴∠F=∠EBC,
∴tan∠F==tan∠EBC==,
设CD=x,则BC=2x,
∴BD=x,
∴OC=OB=x,
∴OF=2OC=x,
在Rt△OCF中,OC2+OF2=CF2,
∴,
解得x=4或x=﹣(舍去),
∴CD=4,
∴OF=4,OA=2,
∴AF=OF﹣OA=2.
9.(1)证明:连接OA,
∵OA=OB,
∴∠OAB=∠OBA,
∵BC为⊙O的直径,
∴∠CAB=90°,
∴∠ACB+∠ABC=90°,
∵∠ADB=∠ACB=∠PAB,
∴∠PAB+∠OAB=90°,
∴∠OAP=90°,
∴AP为⊙O的切线;
(2)解:∵∠ADB=∠ACB,
∴tan∠ADB=tan∠ACB=,
∵AB=6,
∴AC=8,
∴BC==10,
∴OB=5,
过B作BF⊥AP于F,
∵∠ADB=∠BAF,
∴tan∠ADB=tan∠BAF=,
∴设AF=4k,BF=3k,
∴AB=5k=6,
∴k=,
∴BF=,
∵OA⊥AP,BF⊥AP,
∴BF∥OA,
∴△PBF∽△POA,
∴,
∴,
∴PB=.
10.证明:(1)连结OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BOC=∠A+∠OCA=2∠OAC,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)①∵AB=4,
∴OB=BF=OC=2,
∴OF=4,
∵BE∥OC,
∴,
∴BE=1,
故答案为:1;
②当∠CAB的度数为30°时,四边形ACFD是菱形,
理由:∵∠CAB=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠CAB=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
,
∴△ACB≌△ADB(AAS),
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形.
故答案为:30°.
