2020-2021学年苏科版八年级数学下册9.4矩形、菱形、正方形 矩形、菱形 提高教案
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册9.4矩形、菱形、正方形 矩形、菱形 提高教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 14:11:13 | ||
图片预览

文档简介
教学内容
矩形、菱形提高
教学目标
掌握矩形和菱形的性质及应用
重点
特殊三角形的应用
难点
灵活运用
教学过程
知识梳理:
矩形、菱形都是特殊的平行四边形,他们除了具有平行四边形的一切性质外,还有各自的特殊性质
矩形的特殊性体现在:①矩形的四个角都是直角;②矩形的对角线相等;
菱形的特殊性体现在:①菱形的四条边相等;②菱形的对角线互相垂直平分;③每一条对角线平分一组对角
连接对角线,矩形和菱形就可以得到特殊三角形(如等腰三角形、直角三角形)。因此,解矩形、菱形问题时,要注意特殊三角形性质的运用
例题精讲:
例1:如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于点E,∠CAE=15°,则∠BOE=
例2:如图,四边形ABCD是菱形,△AEF是正三角形,点E,F分别在边BC,CD上,且AB=AE,则∠B=
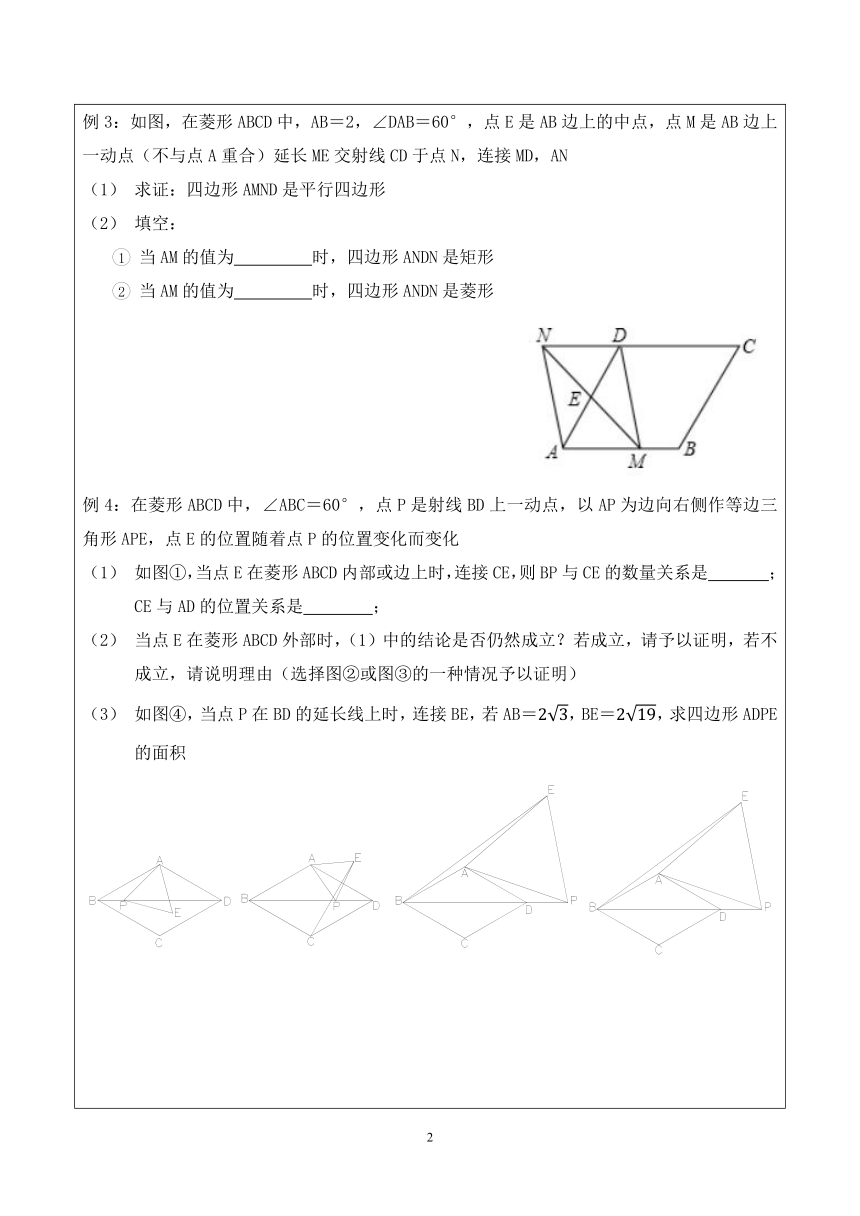
例3:如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AB边上的中点,点M是AB边上一动点(不与点A重合)延长ME交射线CD于点N,连接MD,AN
求证:四边形AMND是平行四边形
填空:
当AM的值为
时,四边形ANDN是矩形
当AM的值为
时,四边形ANDN是菱形
例4:在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边三角形APE,点E的位置随着点P的位置变化而变化
如图①,当点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是
;CE与AD的位置关系是
;
当点E在菱形ABCD外部时,(1)中的结论是否仍然成立?若成立,请予以证明,若不成立,请说明理由(选择图②或图③的一种情况予以证明)
如图④,当点P在BD的延长线上时,连接BE,若AB=,BE=,求四边形ADPE的面积
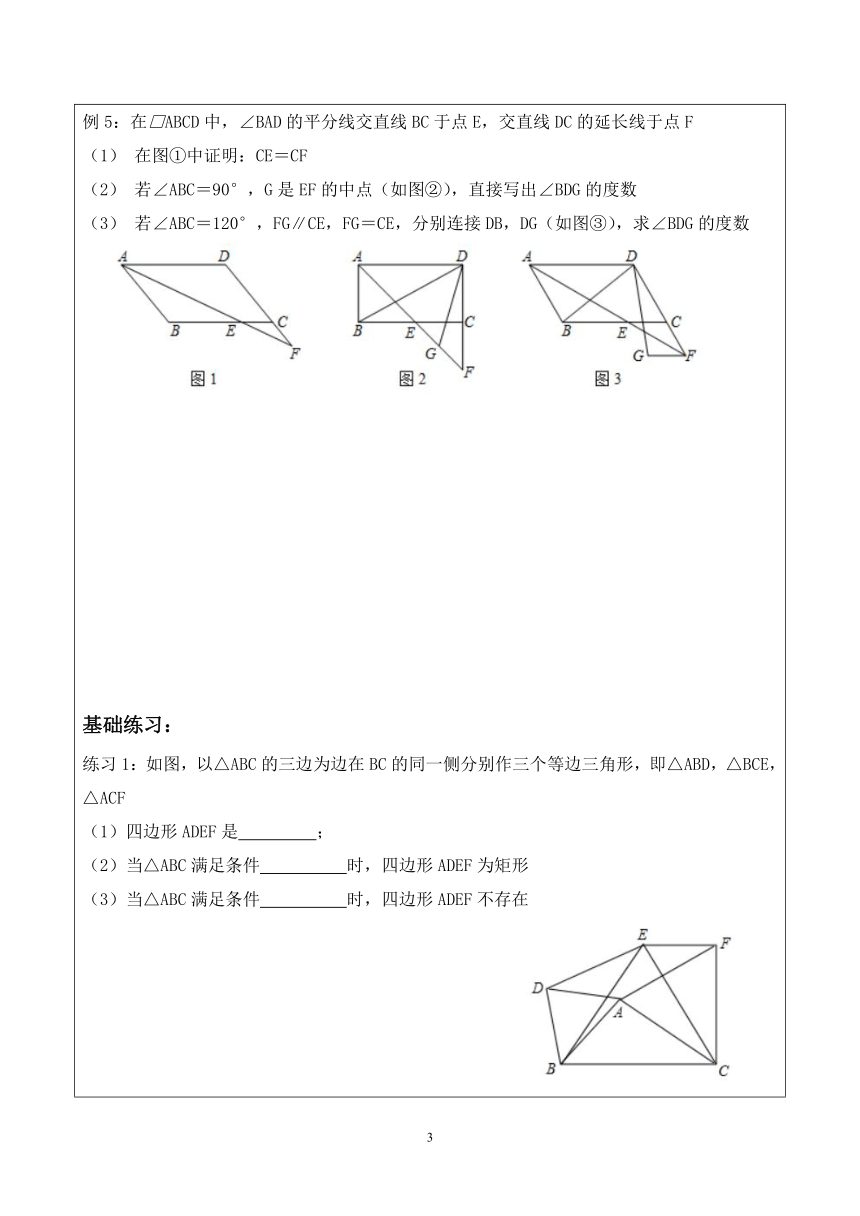
例5:在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F
在图①中证明:CE=CF
若∠ABC=90°,G是EF的中点(如图②),直接写出∠BDG的度数
若∠ABC=120°,FG∥CE,FG=CE,分别连接DB,DG(如图③),求∠BDG的度数
基础练习:
练习1:如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD,△BCE,△ACF
(1)四边形ADEF是
;
(2)当△ABC满足条件
时,四边形ADEF为矩形
(3)当△ABC满足条件
时,四边形ADEF不存在
练习2:如图,将两张长为8,宽为2的矩形纸片交叉,使重叠部分是一个菱形,容易知道当两张纸片垂直时,菱形的周长有最小值,那么菱形周长的最大值是
练习3:如图,平面直角坐标系中,矩形OABC的顶点A(-6,0),C(0,),将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点处,则B的对应点的坐标为
;
练习4:如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,已知∠BAD=120°,∠EAF=30°,则AB∶AE=
练习5:如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=,∠PBA=,∠PCB=,∠PDC=。若∠APB=80°,∠CPD=50°,则
;
A.
B.
C.
D.
练习6:如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG于FH交于点O,四边形AEOF与四边形CGOH的周长之差为12时,AE=
;
练习7:如图,在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过点C作CE⊥BD于点E,延长AF,EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的是(
)
A.
②③
B.
③④
C.
①②③
D.
②③④
练习8:如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,∠FPC=
;
练习9:如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A,B不重合),矩形PECF的顶点E,F分别在BC,AC上
探究DE与DF的关系,并给予证明
当点P满足什么条件时,线段EF的长最短?
练习10:如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F
求证:四边形ADEF为平行四边形
当点D为AB中点时,□ADEF的形状为
;
延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②。若AD=AG,判断四边形AEGF的形状,并说明理由
(
1
)
矩形、菱形提高
教学目标
掌握矩形和菱形的性质及应用
重点
特殊三角形的应用
难点
灵活运用
教学过程
知识梳理:
矩形、菱形都是特殊的平行四边形,他们除了具有平行四边形的一切性质外,还有各自的特殊性质
矩形的特殊性体现在:①矩形的四个角都是直角;②矩形的对角线相等;
菱形的特殊性体现在:①菱形的四条边相等;②菱形的对角线互相垂直平分;③每一条对角线平分一组对角
连接对角线,矩形和菱形就可以得到特殊三角形(如等腰三角形、直角三角形)。因此,解矩形、菱形问题时,要注意特殊三角形性质的运用
例题精讲:
例1:如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于点E,∠CAE=15°,则∠BOE=
例2:如图,四边形ABCD是菱形,△AEF是正三角形,点E,F分别在边BC,CD上,且AB=AE,则∠B=
例3:如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AB边上的中点,点M是AB边上一动点(不与点A重合)延长ME交射线CD于点N,连接MD,AN
求证:四边形AMND是平行四边形
填空:
当AM的值为
时,四边形ANDN是矩形
当AM的值为
时,四边形ANDN是菱形
例4:在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边三角形APE,点E的位置随着点P的位置变化而变化
如图①,当点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是
;CE与AD的位置关系是
;
当点E在菱形ABCD外部时,(1)中的结论是否仍然成立?若成立,请予以证明,若不成立,请说明理由(选择图②或图③的一种情况予以证明)
如图④,当点P在BD的延长线上时,连接BE,若AB=,BE=,求四边形ADPE的面积
例5:在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F
在图①中证明:CE=CF
若∠ABC=90°,G是EF的中点(如图②),直接写出∠BDG的度数
若∠ABC=120°,FG∥CE,FG=CE,分别连接DB,DG(如图③),求∠BDG的度数
基础练习:
练习1:如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD,△BCE,△ACF
(1)四边形ADEF是
;
(2)当△ABC满足条件
时,四边形ADEF为矩形
(3)当△ABC满足条件
时,四边形ADEF不存在
练习2:如图,将两张长为8,宽为2的矩形纸片交叉,使重叠部分是一个菱形,容易知道当两张纸片垂直时,菱形的周长有最小值,那么菱形周长的最大值是
练习3:如图,平面直角坐标系中,矩形OABC的顶点A(-6,0),C(0,),将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点处,则B的对应点的坐标为
;
练习4:如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,已知∠BAD=120°,∠EAF=30°,则AB∶AE=
练习5:如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=,∠PBA=,∠PCB=,∠PDC=。若∠APB=80°,∠CPD=50°,则
;
A.
B.
C.
D.
练习6:如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG于FH交于点O,四边形AEOF与四边形CGOH的周长之差为12时,AE=
;
练习7:如图,在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过点C作CE⊥BD于点E,延长AF,EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的是(
)
A.
②③
B.
③④
C.
①②③
D.
②③④
练习8:如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,∠FPC=
;
练习9:如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A,B不重合),矩形PECF的顶点E,F分别在BC,AC上
探究DE与DF的关系,并给予证明
当点P满足什么条件时,线段EF的长最短?
练习10:如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F
求证:四边形ADEF为平行四边形
当点D为AB中点时,□ADEF的形状为
;
延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②。若AD=AG,判断四边形AEGF的形状,并说明理由
(
1
)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
