辽宁省铁岭市部分校2021届九年级第六次调研考试数学试题(Word版 含答案)
文档属性
| 名称 | 辽宁省铁岭市部分校2021届九年级第六次调研考试数学试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 12:41:13 | ||
图片预览


文档简介
2020-2021
年中考调研试题数学月考试卷(六)(北师版)
考试时间∶
120
分钟试卷满分∶
150分注意事项;
答题前,考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的学校、班级和姓名;
2.考生须在答题卡上作答,不能在本试题卷上作答,答在本试题卷上无效
3.考试结束,将本试题卷和答题卡一并交回
4.本试题卷共
8页。如缺页、印刷不清,考生须声明,否则后果自负
一、选择题(每小题3
分,共
30
分)
1.如图,在△ABC中,∠C=90°,AC=3,BC=4,则sinB的值是(
)
A.
B.
C.
D.
第1题图
第4题图
2.下列投影是平行投影的是(
)
A.
太阳光下窗户的影子
B.
台灯下书本的影子
C.
在手电筒照射下纸片的影子
D.
路灯下行人的影子
3.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为(
)
A.y=(x+1)2+4
B.y=(x-1)2+4
C.y=(x+1)2+2
D.y=(x-1)2+2
4.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30,则AC的长是(
)
A.1
B.
C.
D.2
反比例函数y=的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围()
A.y>1,
B.0C.
y>2,
D.06.如图,在△ABC中,∠ACB=90,∠A=30°,AB=4,以B为圆心,BC长为半径画弧,交边
AB
于点
D,则的长为(
)
A.
π
B.
C.
D.
第6题图
第7题图
7.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为{
4cm,圆心角为
60°,则图中摆盘的面积是()
A.80πcm2
B.
40πcm2
C.24πcm2
D.2πcm2
8.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=3米,坡顶有一旗杆BC,旗杆顶端B点与A
点有一条彩带相连,若
AB=10米,则旗杆
BC的高度为(
)
A.5米
B.6米
C.8米
D.(3+)米
第8题图
第9题图
第10题图
在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转
90°后得到△AB′C′.则图中阴影部分面积为()
A.
B
C.
D.
10.如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与亥抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为()
A.(0,2)
B.(,0)
C.(0,2)或(,0)
D.以上都不正确
二
填空题∶(每小题3
分,共
24分)
11
在
Rt△ABC中,∠C=90°,AB=2,BC=
,则
sinA
=___
12
已知扇形的弧长为
10πcm,面积为
30π
cm,则扇形的圆心角为____.
13
一元二次方程
2x2-x+1=0的根的情况是
_
14
已知抛物线
y=x?-4x+m与x轴交于A、B两点,若A的坐标是(-1,0),则B的坐标是
15
如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=4,则的长k为
第15题图
第16题图
第17题图
第18题图
16
如图,点
A、B、C在直径为2的⊙O
上,∠BAC=45°,则图中阴影的面积等于
__(结果中保留π).
17
如图,圆锥的母线长
OA为
8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线
OC
中点
B处有一只小虫,蚂蚁要捉小虫,
需要爬行的最短路程为___
18.二次函数
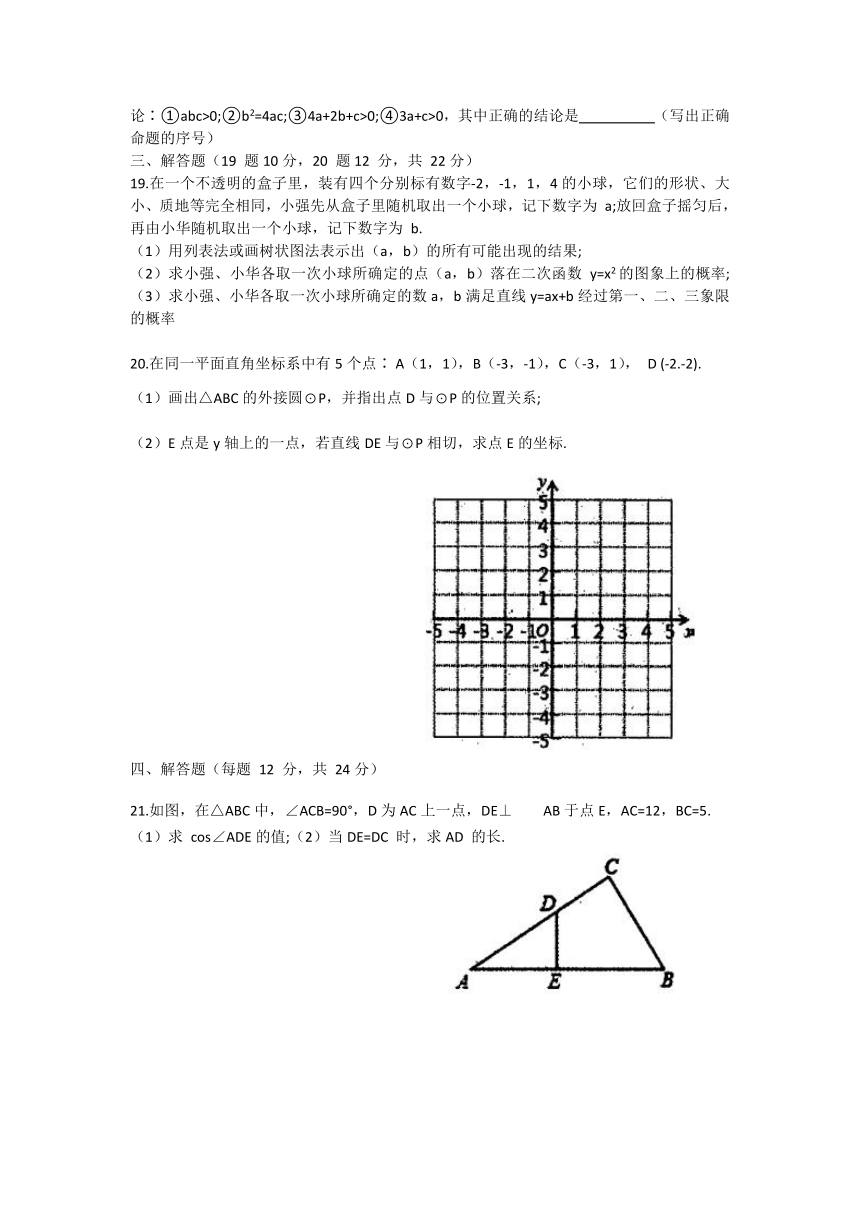
y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列论∶①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是
(写出正确命题的序号)
三、解答题(19
题10分,20
题12
分,共
22分)
19.在一个不透明的盒子里,装有四个分别标有数字-2,-1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为
a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为
b.
(1)用列表法或画树状图法表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数
y=x2的图象上的概率;(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过第一、二、三象限的概率
20.在同一平面直角坐标系中有5个点∶
A(1,1),B(-3,-1),C(-3,1),
D
(-2.-2).
(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)E点是y轴上的一点,若直线DE与⊙P相切,求点E的坐标.
四、解答题(每题
12
分,共
24分)
21.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求
cos∠ADE的值;(2)当DE=DC
时,求AD
的长.
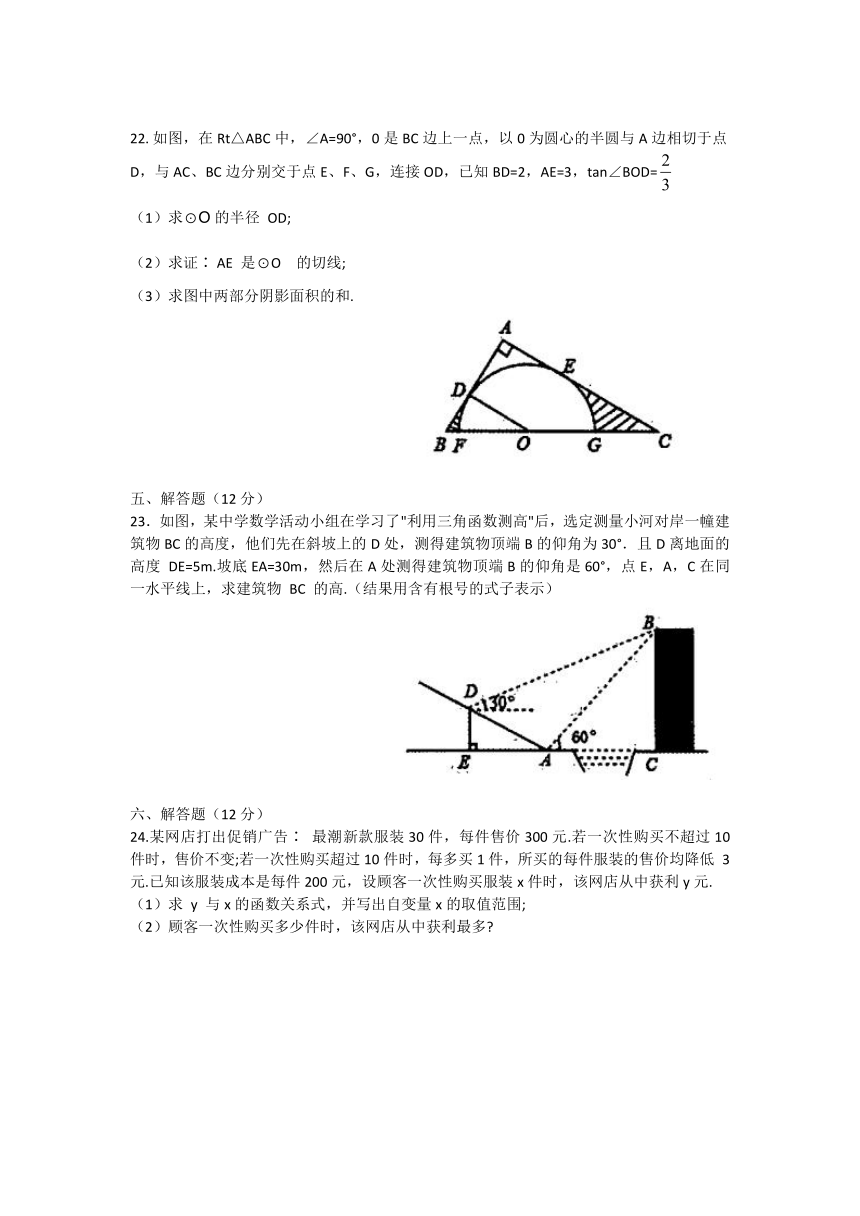
如图,在Rt△ABC中,∠A=90°,0是BC边上一点,以0为圆心的半圆与A边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=
求⊙O的半径
OD;
求证∶
AE
是⊙O
的切线;
(3)求图中两部分阴影面积的和.
五、解答题(12分)
23.如图,某中学数学活动小组在学习了"利用三角函数测高"后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度
DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物
BC
的高.(结果用含有根号的式子表示)
六、解答题(12分)
24.某网店打出促销广告∶
最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低
3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求
y
与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
七、解答题(本题
12
分)
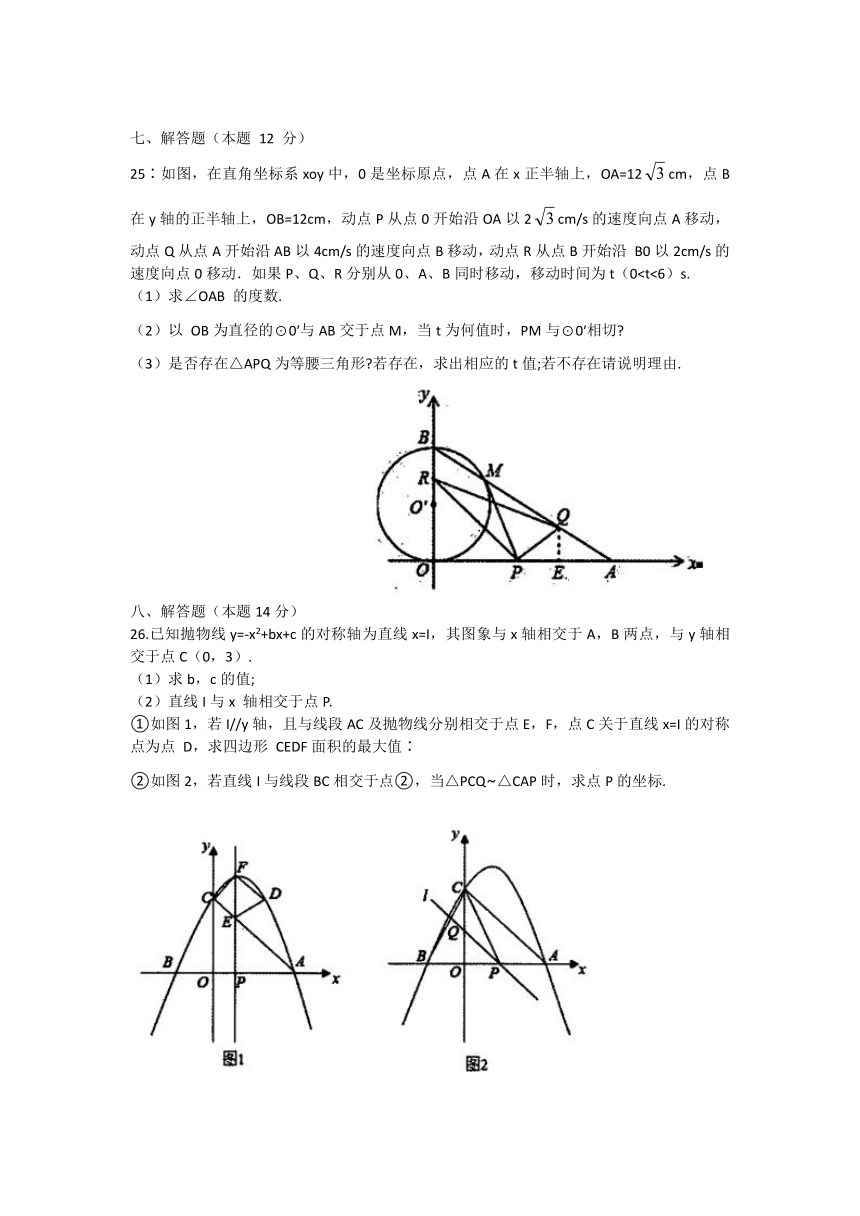
25∶如图,在直角坐标系xoy中,0是坐标原点,点A在x正半轴上,OA=12cm,点B在y轴的正半轴上,OB=12cm,动点P从点0开始沿OA以2cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿
B0以2cm/s的速度向点0移动.如果P、Q、R分别从0、A、B同时移动,移动时间为t(0(1)求∠OAB
的度数.
(2)以
OB为直径的⊙0′与AB交于点M,当t为何值时,PM与⊙0′相切?
(3)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
八、解答题(本题14分)
26.已知抛物线y=-x2+bx+c的对称轴为直线x=I,其图象与x轴相交于A,B两点,与y轴相交于点C(0,3).
(1)求b,c的值;
(2)直线I与x
轴相交于点P.
①如图1,若I//y轴,且与线段AC及抛物线分别相交于点E,F,点C关于直线x=I的对称点为点
D,求四边形
CEDF面积的最大值∶
②如图2,若直线I与线段BC相交于点②,当△PCQ~△CAP时,求点P的坐标.
年中考调研试题数学月考试卷(六)(北师版)
考试时间∶
120
分钟试卷满分∶
150分注意事项;
答题前,考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的学校、班级和姓名;
2.考生须在答题卡上作答,不能在本试题卷上作答,答在本试题卷上无效
3.考试结束,将本试题卷和答题卡一并交回
4.本试题卷共
8页。如缺页、印刷不清,考生须声明,否则后果自负
一、选择题(每小题3
分,共
30
分)
1.如图,在△ABC中,∠C=90°,AC=3,BC=4,则sinB的值是(
)
A.
B.
C.
D.
第1题图
第4题图
2.下列投影是平行投影的是(
)
A.
太阳光下窗户的影子
B.
台灯下书本的影子
C.
在手电筒照射下纸片的影子
D.
路灯下行人的影子
3.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为(
)
A.y=(x+1)2+4
B.y=(x-1)2+4
C.y=(x+1)2+2
D.y=(x-1)2+2
4.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30,则AC的长是(
)
A.1
B.
C.
D.2
反比例函数y=的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围()
A.y>1,
B.0
y>2,
D.0
AB
于点
D,则的长为(
)
A.
π
B.
C.
D.
第6题图
第7题图
7.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为{
4cm,圆心角为
60°,则图中摆盘的面积是()
A.80πcm2
B.
40πcm2
C.24πcm2
D.2πcm2
8.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=3米,坡顶有一旗杆BC,旗杆顶端B点与A
点有一条彩带相连,若
AB=10米,则旗杆
BC的高度为(
)
A.5米
B.6米
C.8米
D.(3+)米
第8题图
第9题图
第10题图
在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转
90°后得到△AB′C′.则图中阴影部分面积为()
A.
B
C.
D.
10.如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与亥抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为()
A.(0,2)
B.(,0)
C.(0,2)或(,0)
D.以上都不正确
二
填空题∶(每小题3
分,共
24分)
11
在
Rt△ABC中,∠C=90°,AB=2,BC=
,则
sinA
=___
12
已知扇形的弧长为
10πcm,面积为
30π
cm,则扇形的圆心角为____.
13
一元二次方程
2x2-x+1=0的根的情况是
_
14
已知抛物线
y=x?-4x+m与x轴交于A、B两点,若A的坐标是(-1,0),则B的坐标是
15
如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=4,则的长k为
第15题图
第16题图
第17题图
第18题图
16
如图,点
A、B、C在直径为2的⊙O
上,∠BAC=45°,则图中阴影的面积等于
__(结果中保留π).
17
如图,圆锥的母线长
OA为
8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线
OC
中点
B处有一只小虫,蚂蚁要捉小虫,
需要爬行的最短路程为___
18.二次函数
y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列论∶①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是
(写出正确命题的序号)
三、解答题(19
题10分,20
题12
分,共
22分)
19.在一个不透明的盒子里,装有四个分别标有数字-2,-1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为
a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为
b.
(1)用列表法或画树状图法表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数
y=x2的图象上的概率;(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过第一、二、三象限的概率
20.在同一平面直角坐标系中有5个点∶
A(1,1),B(-3,-1),C(-3,1),
D
(-2.-2).
(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)E点是y轴上的一点,若直线DE与⊙P相切,求点E的坐标.
四、解答题(每题
12
分,共
24分)
21.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求
cos∠ADE的值;(2)当DE=DC
时,求AD
的长.
如图,在Rt△ABC中,∠A=90°,0是BC边上一点,以0为圆心的半圆与A边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=
求⊙O的半径
OD;
求证∶
AE
是⊙O
的切线;
(3)求图中两部分阴影面积的和.
五、解答题(12分)
23.如图,某中学数学活动小组在学习了"利用三角函数测高"后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度
DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物
BC
的高.(结果用含有根号的式子表示)
六、解答题(12分)
24.某网店打出促销广告∶
最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低
3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求
y
与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
七、解答题(本题
12
分)
25∶如图,在直角坐标系xoy中,0是坐标原点,点A在x正半轴上,OA=12cm,点B在y轴的正半轴上,OB=12cm,动点P从点0开始沿OA以2cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿
B0以2cm/s的速度向点0移动.如果P、Q、R分别从0、A、B同时移动,移动时间为t(0
的度数.
(2)以
OB为直径的⊙0′与AB交于点M,当t为何值时,PM与⊙0′相切?
(3)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
八、解答题(本题14分)
26.已知抛物线y=-x2+bx+c的对称轴为直线x=I,其图象与x轴相交于A,B两点,与y轴相交于点C(0,3).
(1)求b,c的值;
(2)直线I与x
轴相交于点P.
①如图1,若I//y轴,且与线段AC及抛物线分别相交于点E,F,点C关于直线x=I的对称点为点
D,求四边形
CEDF面积的最大值∶
②如图2,若直线I与线段BC相交于点②,当△PCQ~△CAP时,求点P的坐标.
同课章节目录
