北师大版七年级数学下册1.6 完全平方公式习题课件(19张ppt)
文档属性
| 名称 | 北师大版七年级数学下册1.6 完全平方公式习题课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 295.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 13:18:21 | ||
图片预览






文档简介
第一章 整式的乘除
6 完全平方公式
完全平方公式
两数的和(或差)的________,等于它们的__________加上(或减去)它们积的_____倍.用字母可表示为(a+b)2=a2+_________+b2或(a-b)2=a2-2ab+b2.
平方
平方和
2
2ab
1.设A,B都是多项式,如果A=B2,则A是一个完全平方式,已知多项式x2-mx+9是完全平方式.
(1)这个多项式有什么特点?
(2)你能根据上述条件求m的值吗?试试看.
答:(1)因为9=32,根据完全平方公式的定义可知,这个多项式有两个特点:一是这个多项式是三项式;二是-m等于x与3的乘积的2倍或-m等于-x与3乘积的2倍.
(2)∵x2-mx+9是完全平方式,
∴-mx=±2·x·3,
解得m=±6.
2.(2020年哈尔滨香坊区月考)下列运算正确的是 ( )
A.(a+1)2=a2+1 B.a-2=-a2
C.a(a-1)=a2-1 D.(a-2)2=a2-4a+4
D
知识点1 完全平方公式
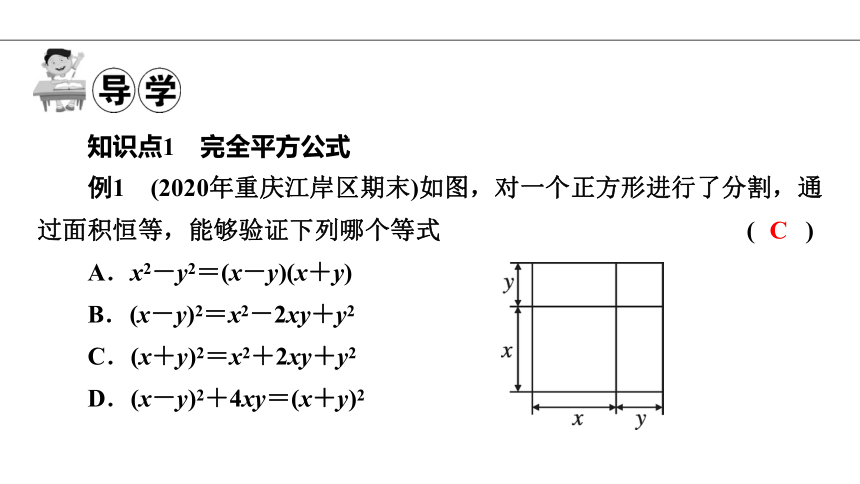
例1 (2020年重庆江岸区期末)如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式 ( )
A.x2-y2=(x-y)(x+y)
B.(x-y)2=x2-2xy+y2
C.(x+y)2=x2+2xy+y2
D.(x-y)2+4xy=(x+y)2
C
3.(2020年常德期末)下列计算正确的是 ( )
A.(x2)3=x9
B.(-x)2·x=x3
C.(-2ab2)2=-4a2b4
D.(x-y)2=x2-y2
B
知识点2 利用完全平方公式计算
例2 利用完全平方公式计算:
(1)(3a-b)2;
解:原式=(3a)2-2×3a·b+b2=9a2-6ab+b2.
(3)(x+2)2-(x+1)(x-1).
解:原式=x2+4x+4-(x2-1)
=x2+4x+4-x2+1
=4x+5.
4.(2020年邳州期中)(-x-2y)2=__________________.
5.计算下列各题:
(1)(2x-3y)2;
解:原式=(2x)2-2·2x·3y+(-3y)2=4x2-12xy+9y2.
(2)(x+y)(x+y)(x2+y2).
解:原式=(x2+2xy+y2)(x2+y2)
=(x2+y2)2+2xy(x2+y2)
=x4+2x2y2+y4+2x3y+2xy3.
x2+4xy+4y2
归纳总结:利用完全平方公式计算的步骤仍可概括为“一变(把能变为完全平方公式的算式变形为与完全平方公式相同的形式)、二套(套用完全平方公式计算)、三计算(在套用完全平方公式后,对于还能继续计算的算式要继续计算)”.
【第一关】
1.(2020年广元模拟)下列运算正确的是 ( )
A.a3+a4=a7 B.a8÷a2=a4
C.a2·a3=a5 D.(a+b)2=a2+b2
C
2.(2020年深圳福田区校级期中)如果x2+8x+m2是一个完全平方式,那么m的值是 ( )
A.4 B.-4
C.±4 D.±8
C
3.(2020年徐州期中)如图,在边长为6.75 cm的正方形纸片上,剪去一个边长为3.25 cm的小正方形,则图中阴影部分的面积为______ cm2.
35
【第二关】
4.(2020年绍兴柯桥区期末)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如,图1可以用来解释(a+b)2-(a-b)2=4ab.那么通过图2面积的计算,验证了一个恒等式,此等式是 ( )
A.a2-b2=(a+b)(a-b)
B.(a-b)(a+2b)=a2+ab-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
C
5.(2020年淮南田家庵区期末)如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为______.
?
6.计算下列各题:
(1)(3a+b)2;
解:原式=(3a)2+2×(3a)·b+b2 =9a2+6ab+b2.
(2)(-3+2a)2;
解:原式=(-3)2+2×(-3)·2a+(2a)2=9-12a+4a2.
(3)(x-2y)2;
解:原式=x2-2·x·2y+(2y)2 =x2-4xy+4y2.
(4)(-2x-3y)2.
解:原式=(-2x)2+2·(-2x)(-3y)+(-3y)2=4x2+12xy+9y2.
【第三关】
7.已知x2+x-5=0,求代数式(x-1)2-x(x-3)+(x+2)(x-2)的值.
解:(x-1)2-x(x-3)+(x+2)(x-2)=x2-2x+1-x2+3x+x2-4=x2+x-3.
∵x2+x-5=0,∴x2+x=5,
∴原式=5-3=2.
6 完全平方公式
完全平方公式
两数的和(或差)的________,等于它们的__________加上(或减去)它们积的_____倍.用字母可表示为(a+b)2=a2+_________+b2或(a-b)2=a2-2ab+b2.
平方
平方和
2
2ab
1.设A,B都是多项式,如果A=B2,则A是一个完全平方式,已知多项式x2-mx+9是完全平方式.
(1)这个多项式有什么特点?
(2)你能根据上述条件求m的值吗?试试看.
答:(1)因为9=32,根据完全平方公式的定义可知,这个多项式有两个特点:一是这个多项式是三项式;二是-m等于x与3的乘积的2倍或-m等于-x与3乘积的2倍.
(2)∵x2-mx+9是完全平方式,
∴-mx=±2·x·3,
解得m=±6.
2.(2020年哈尔滨香坊区月考)下列运算正确的是 ( )
A.(a+1)2=a2+1 B.a-2=-a2
C.a(a-1)=a2-1 D.(a-2)2=a2-4a+4
D
知识点1 完全平方公式
例1 (2020年重庆江岸区期末)如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式 ( )
A.x2-y2=(x-y)(x+y)
B.(x-y)2=x2-2xy+y2
C.(x+y)2=x2+2xy+y2
D.(x-y)2+4xy=(x+y)2
C
3.(2020年常德期末)下列计算正确的是 ( )
A.(x2)3=x9
B.(-x)2·x=x3
C.(-2ab2)2=-4a2b4
D.(x-y)2=x2-y2
B
知识点2 利用完全平方公式计算
例2 利用完全平方公式计算:
(1)(3a-b)2;
解:原式=(3a)2-2×3a·b+b2=9a2-6ab+b2.
(3)(x+2)2-(x+1)(x-1).
解:原式=x2+4x+4-(x2-1)
=x2+4x+4-x2+1
=4x+5.
4.(2020年邳州期中)(-x-2y)2=__________________.
5.计算下列各题:
(1)(2x-3y)2;
解:原式=(2x)2-2·2x·3y+(-3y)2=4x2-12xy+9y2.
(2)(x+y)(x+y)(x2+y2).
解:原式=(x2+2xy+y2)(x2+y2)
=(x2+y2)2+2xy(x2+y2)
=x4+2x2y2+y4+2x3y+2xy3.
x2+4xy+4y2
归纳总结:利用完全平方公式计算的步骤仍可概括为“一变(把能变为完全平方公式的算式变形为与完全平方公式相同的形式)、二套(套用完全平方公式计算)、三计算(在套用完全平方公式后,对于还能继续计算的算式要继续计算)”.
【第一关】
1.(2020年广元模拟)下列运算正确的是 ( )
A.a3+a4=a7 B.a8÷a2=a4
C.a2·a3=a5 D.(a+b)2=a2+b2
C
2.(2020年深圳福田区校级期中)如果x2+8x+m2是一个完全平方式,那么m的值是 ( )
A.4 B.-4
C.±4 D.±8
C
3.(2020年徐州期中)如图,在边长为6.75 cm的正方形纸片上,剪去一个边长为3.25 cm的小正方形,则图中阴影部分的面积为______ cm2.
35
【第二关】
4.(2020年绍兴柯桥区期末)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如,图1可以用来解释(a+b)2-(a-b)2=4ab.那么通过图2面积的计算,验证了一个恒等式,此等式是 ( )
A.a2-b2=(a+b)(a-b)
B.(a-b)(a+2b)=a2+ab-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
C
5.(2020年淮南田家庵区期末)如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为______.
?
6.计算下列各题:
(1)(3a+b)2;
解:原式=(3a)2+2×(3a)·b+b2 =9a2+6ab+b2.
(2)(-3+2a)2;
解:原式=(-3)2+2×(-3)·2a+(2a)2=9-12a+4a2.
(3)(x-2y)2;
解:原式=x2-2·x·2y+(2y)2 =x2-4xy+4y2.
(4)(-2x-3y)2.
解:原式=(-2x)2+2·(-2x)(-3y)+(-3y)2=4x2+12xy+9y2.
【第三关】
7.已知x2+x-5=0,求代数式(x-1)2-x(x-3)+(x+2)(x-2)的值.
解:(x-1)2-x(x-3)+(x+2)(x-2)=x2-2x+1-x2+3x+x2-4=x2+x-3.
∵x2+x-5=0,∴x2+x=5,
∴原式=5-3=2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
