四年级数学下册课件-2.3 探索与发现:三角形内角和北师大版(共24张PPT)
文档属性
| 名称 | 四年级数学下册课件-2.3 探索与发现:三角形内角和北师大版(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:44:40 | ||
图片预览



文档简介
三角形的内角和
不对。我有一个大钝角,所以我的内角和才最大!
我的三角形小,那我的内角和就小喽……
我的三角形最大,所以我的内角和最大!
(一)创设情境,设疑导新
1、什么是三角形的内角?
1
2
3
∠1+∠2+∠3
2、什么是三角形的内角和?
∠1,
∠2,
∠3
思考:
量一量
探究一(对学):
合作要求:
(1)找到自己的合作伙伴。 (2)用量角器测量你们手中的三角形每个内角的度数,并算出三个角度数之和。 (3)一人测量,一人做好记录。
(二)动手实践,发现新知
∠1
∠2
∠3
内角和
发现规律
锐角三角形
直角三角形
钝角三角形
锐角三角形
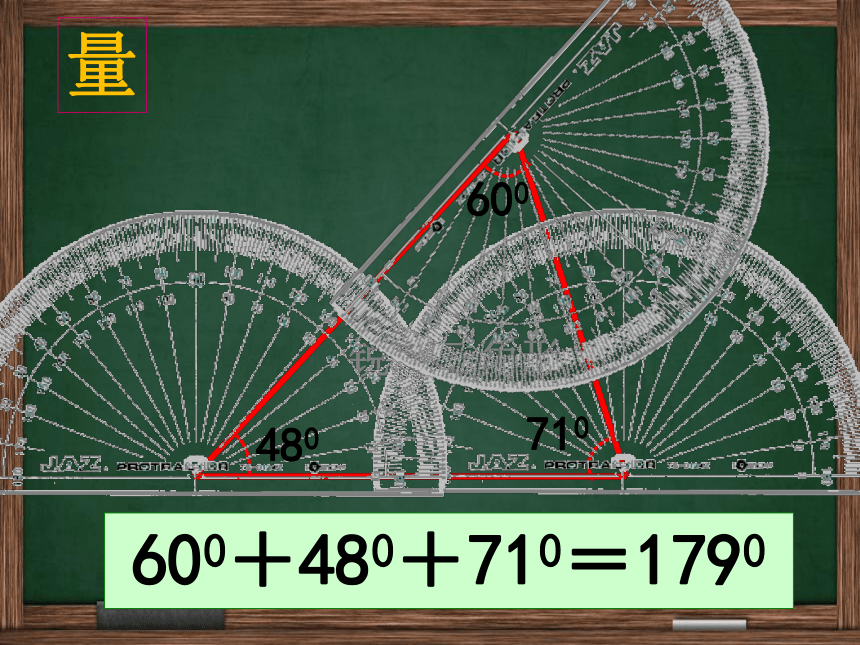
量
480
710
600
600+480+710=1790
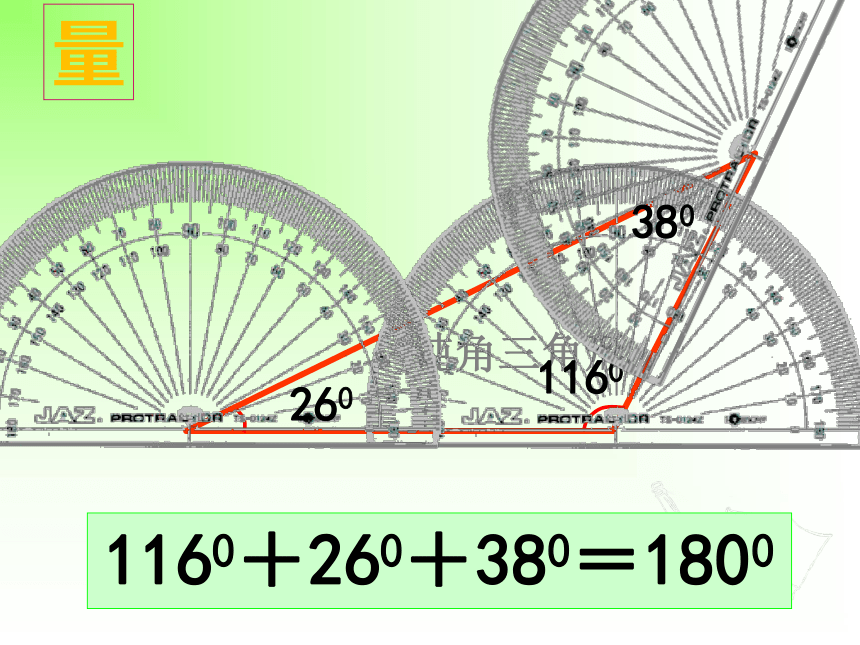
钝角三角形
260
1160
1160+260+380=1800
380
量
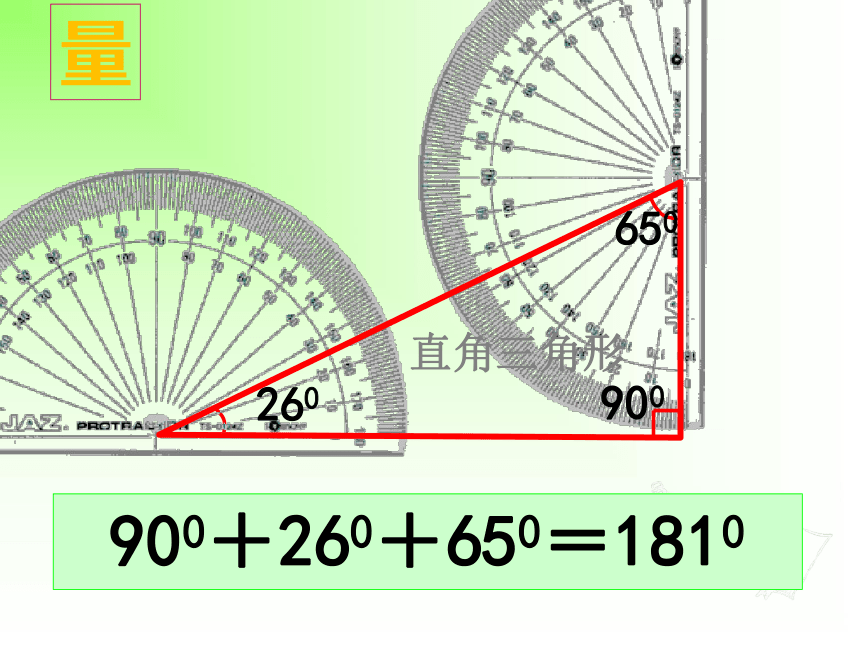
直角三角形
260
900
650
量
900+260+650=1810
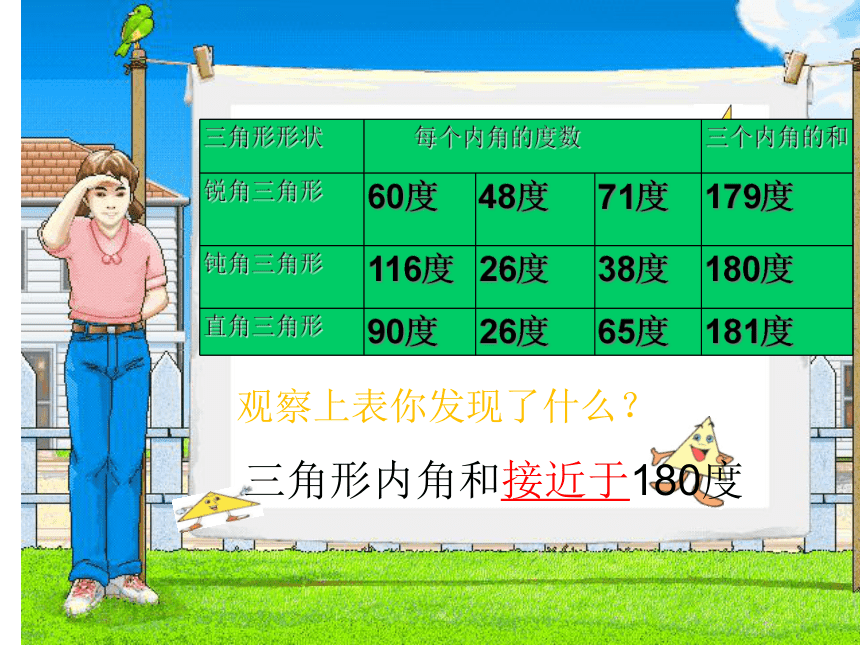
三角形形状
每个内角的度数
三个内角的和
锐角三角形
60度
48度
71度
179度
钝角三角形
116度
26度
38度
180度
直角三角形
90度
26度
65度
181度
观察上表你发现了什么?
三角形内角和接近于180度
*
(1)剪一剪、拼一拼
探究二(小组合作):选用自己喜欢的方法验证
学法导航:在剪之前要分别在三个角上标好角1、角2和角3。然后剪下三个角,把三个角的一条边、顶点重合。
(2)折一折、拼一拼
学法导航:比如折的是一个锐角三角形,可以先把它上面的一个角折下,顶点和
下面的边重合,再分别把左边、右边
的角往里折,三个角的顶点要
重合。
拼一拼:
3
平角:1800
平角:1800
平角:1800
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折:
平角:180°
三角形不论大小,内角和都是180度。
无论是锐角三角形,直角三角形还是钝角三角形,它们的内角和都是180°。
发现秘密
1
1
1
2
2
2
3
3
3
①三角形越大,它的内角和就越大。 ( )
②一个三角形的三个内角度数是:70°,64°, 45°。 ?( )
③一个三角形至少有两个角是锐角。 ( )
④钝角三角形的内角和大于锐角三角形的内角和。 ( )
(对的画“√”,错的画“×”)
第一关:
请你来当数学小判官
(三)应用新知,解决问题
在一个三角形,∠1=140°,
∠3=25°,求∠2的度数.
第二关:
求出三角形各个角的度数。
第三关:
算一算,内角和是多少?
拓展练习
返回
(四)评价总结,交流反思
同学们,今天你学到了哪些知识?你是怎样获取这些知识的?说一说吧!
帕斯卡,法国数学家,物理学家,近代概率论的奠基者。早在300多年前这位法国的科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
数学文化
(五)延伸知识,激发兴趣
谢谢!
不对。我有一个大钝角,所以我的内角和才最大!
我的三角形小,那我的内角和就小喽……
我的三角形最大,所以我的内角和最大!
(一)创设情境,设疑导新
1、什么是三角形的内角?
1
2
3
∠1+∠2+∠3
2、什么是三角形的内角和?
∠1,
∠2,
∠3
思考:
量一量
探究一(对学):
合作要求:
(1)找到自己的合作伙伴。 (2)用量角器测量你们手中的三角形每个内角的度数,并算出三个角度数之和。 (3)一人测量,一人做好记录。
(二)动手实践,发现新知
∠1
∠2
∠3
内角和
发现规律
锐角三角形
直角三角形
钝角三角形
锐角三角形
量
480
710
600
600+480+710=1790
钝角三角形
260
1160
1160+260+380=1800
380
量
直角三角形
260
900
650
量
900+260+650=1810
三角形形状
每个内角的度数
三个内角的和
锐角三角形
60度
48度
71度
179度
钝角三角形
116度
26度
38度
180度
直角三角形
90度
26度
65度
181度
观察上表你发现了什么?
三角形内角和接近于180度
*
(1)剪一剪、拼一拼
探究二(小组合作):选用自己喜欢的方法验证
学法导航:在剪之前要分别在三个角上标好角1、角2和角3。然后剪下三个角,把三个角的一条边、顶点重合。
(2)折一折、拼一拼
学法导航:比如折的是一个锐角三角形,可以先把它上面的一个角折下,顶点和
下面的边重合,再分别把左边、右边
的角往里折,三个角的顶点要
重合。
拼一拼:
3
平角:1800
平角:1800
平角:1800
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折:
平角:180°
三角形不论大小,内角和都是180度。
无论是锐角三角形,直角三角形还是钝角三角形,它们的内角和都是180°。
发现秘密
1
1
1
2
2
2
3
3
3
①三角形越大,它的内角和就越大。 ( )
②一个三角形的三个内角度数是:70°,64°, 45°。 ?( )
③一个三角形至少有两个角是锐角。 ( )
④钝角三角形的内角和大于锐角三角形的内角和。 ( )
(对的画“√”,错的画“×”)
第一关:
请你来当数学小判官
(三)应用新知,解决问题
在一个三角形,∠1=140°,
∠3=25°,求∠2的度数.
第二关:
求出三角形各个角的度数。
第三关:
算一算,内角和是多少?
拓展练习
返回
(四)评价总结,交流反思
同学们,今天你学到了哪些知识?你是怎样获取这些知识的?说一说吧!
帕斯卡,法国数学家,物理学家,近代概率论的奠基者。早在300多年前这位法国的科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
数学文化
(五)延伸知识,激发兴趣
谢谢!
