7.2.2 用坐标表示平移 课件(30张)
文档属性
| 名称 | 7.2.2 用坐标表示平移 课件(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 12:35:16 | ||
图片预览








文档简介
用坐标表示平移
情境引入
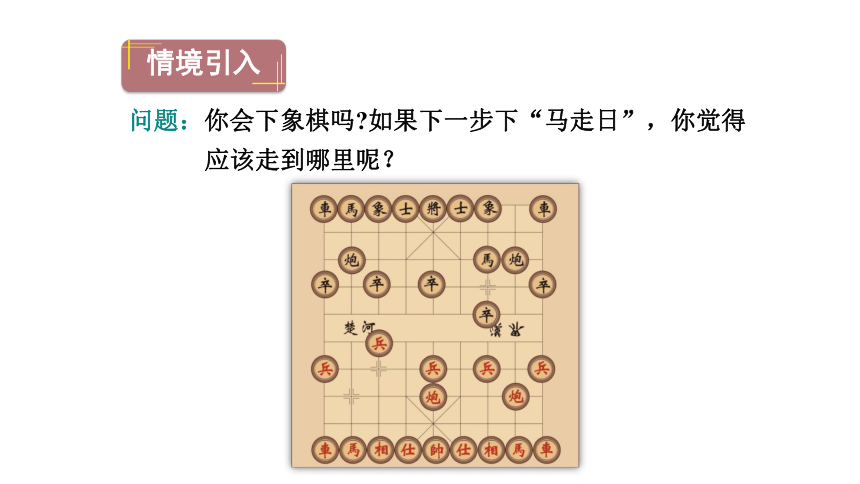
问题:你会下象棋吗?如果下一步下“马走日”,你觉得应该走到哪里呢?
新知讲解
平面直角坐标系中点的平移
1
你还记得什么叫平移吗?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行(或共线)且相等.
3.对应线段平行(或共线)且相等,对应角相等.
图形平移的性质是什么?
新知讲解
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
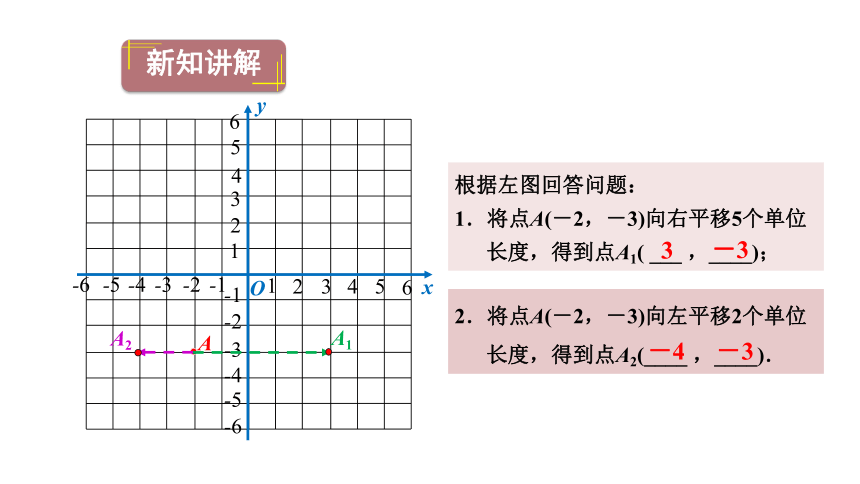
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ ,____);
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ ,____).
A1
-4
-3
3
-3
A2
y
x
新知讲解
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
-2
-5
-2
-1
A4
y
x
新知讲解
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
例1 平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2)
C.(-6,-1) D.(0,-1)
新知应用
C
点的平移变换:左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.
【解析】点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
【变式】1.若将点A向右平移5个单位长度后得到的点为(3,-3),则把点A向上平移4个单位长度后得到的点的坐标为________.
2.平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
(-2,1)
新知演练
D
跟踪练习
1.点A(-3,3)向左平移5个单位长度,得到对应点坐标是 .
(-8,3)
3.点A1(6,3)是由点A(-1,3)经过 得到的,点B(5,2)向 得到B1(7,2).
向右平移7个单位长度
右平移2个单位长度
2.将点A(3,2)向下平移2个单位长度,向右平移4个单位长度得到A1,则A1的坐标 为________.
(7,0)
4.将点P(m+1,n-2)向上平移3个单位长度,得到点Q(2,1-n),则点A(m,n)坐标为 .
(1,0)
跟踪练习
5.将点P(2m+3,m-2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,-2) B.(3,0) C.(7,0) D.(9,1)
6.在平面直角坐标中,点A(1,2)平移后的坐标是A′(-3,3),按照同样的规律平移其它点,则( )变换符合这种要求.
A.(3,2)→(4,-2)
B.(-1,0)→(-5,-4)
C.(2.5,-????????)→(-1.5,????3)
D.(1.2,5)→(-3.2,6)
?
A
C
新知讲解
平面直角坐标系中图形的平移
2
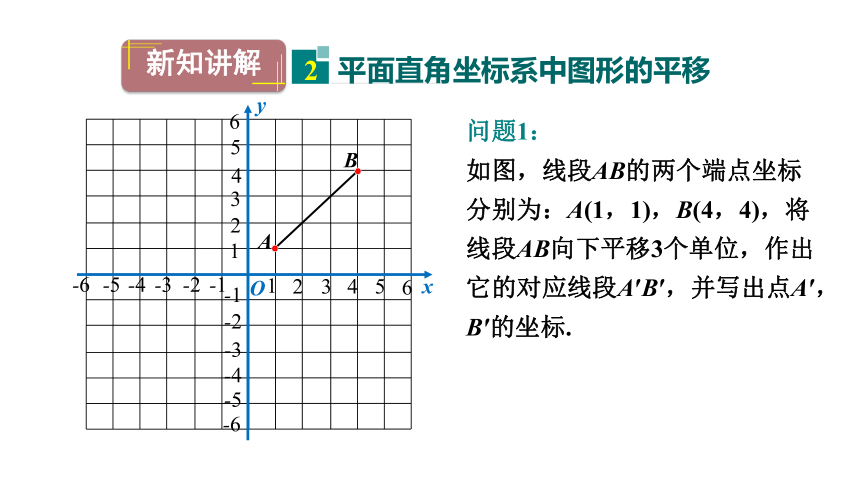
问题1:
如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),将线段AB向下平移3个单位,作出它的对应线段A′B′,并写出点A′,B′的坐标.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
x
y
B
A
新知讲解
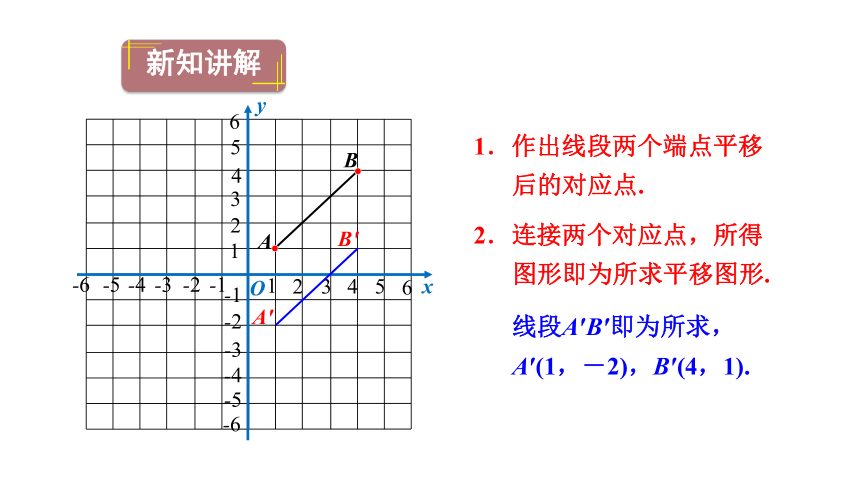
1.作出线段两个端点平移后的对应点.
2.连接两个对应点,所得图形即为所求平移图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
x
B
A
y
A′
B′
线段A′B′即为所求,
A′(1,-2),B′(4,1).
新知讲解
A
B
C
A1
B1
1.三角形ABC是怎样移动得到三角形A1B1C1?
向右平移5个单位
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
新知讲解
A
B
C
A1
B1
2.写出三角形ABC与三角形A1B1C1各点的坐标,它们有怎样的变化?
A(-1,3),B(-4,2), C(-2,1),
A1(4,3),B1(1,2),C1(3,1);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
平移后的对应点的横坐标增加了5,纵坐标不变;
新知讲解
A
B
C
A1
B1
3.如果三角形A1B1C1向下平移4个单位,得到三角形 A2B2C2,写出各点的坐标,它们有怎样的变化?
A2(4,-1),B2(1,-2),C2(3,-3);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
平移后的对应点的横坐标不变,纵坐标减少了4.
A2
B2
C2
新知讲解
A
B
C
A1
B1
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题3:
三角形 ABC能否在坐标平面内直接平移后得到三角形 A2B2C2 ?
C1
一般地,图形经过两次平移后得到的图形,可以通过原来的图形作一次平移得到.
A2
B2
C2
通过对以上问题的探讨,你能说出图形平移的规律吗?
新知讲解
向右平移a个单位
原图形上的点P(x,y)
向左平移a个单位
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
向下平移b个单位
P3(x,y+b)
P4(x,y-b)
图形的平移规律
图形的平移与图形上某一点的平移规律是一致的,因此,图形的平移问题可以转化为某一点的平移问题.
新知讲解
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
(x+a,y+b)
(x+a,y-b)
(x-a,y+b)
(x-a,y-b)
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
图形的平移方向和平移距离
图形上对应点的坐标
例2 如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
新知应用
1
y
O
1
A
B
C
A1
B1
C1
解:三角形A1B1C1如图所示,
各点的坐标分别为:A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
x
(1)请画出上述平移后的三角形A1B1C1,并写出点A、C、
A1、C1的坐标;
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
解:连接AA1,CC1,
新知应用
1
y
O
1
A
B
C
A1
B1
C1
x
=????????×2×7=7=
?
【变式】1.将一个三角形的三个顶点分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别为( )
A.(6,0), (3,2), (8,-6)
B.(-1,-5), (2,-7), (3,-1)
C.(1,5), (2,-7), (-3,1)
D.(-1,5), (2,-7), (-3,1)
A
新知演练
【变式】2.如图,△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出△A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
解:(1)△A1B1C1是由△ABC向左平移3个单位,再向上平移1个单位所得,则
A1(-1,2),B1(2,4),C1 (0,5);
(2)如图,△ABC的面积
=3×3-????????×1×3-????????×1×2-????????×2×3
=3.5
?
新知演练
跟踪练习
1.在6×6方格中,将图①中的图形甲平移后位置如图②所示,则图形甲的平移方法正确的是( )
A.先向左平移1格,再向下平移2格
B.先向右平移3格,再向下平移2格
C.先向右平移1格,再向下平移3格
D.先向右平移2格,再向下平移3格
C
跟踪练习
2.线段CD是由线段AB平移得到的.其中点A(-1,4)的对应点为C(4,4),则点B(-4,-1)的对应点D的坐标为________.
(1,-1)
3.(1)已知线段MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为______________________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为_________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
4.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1. 求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);
B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
A
跟踪练习
拓展练习
1.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
解:(1)如图所示:
A′(0,4)、B′(-1,1)、C′(3,1);
(2)S△ABC=????????×(3+1)×3=6
?
A′
B′
C′
拓展练习
1.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
解:设点P坐标为(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得????????×4×|y+2|=6,
解得y=1或y=-5,
所以点P的坐标为(0,1)或(0,-5).
?
拓展练习
2.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
(2)向右平移5个单位,再向上平移3个单位.
拓展练习
2.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(3)求△BCF的面积.
解:作CH⊥OF于H.设F(m,0),
∵S△AOF=S四边形AOHC+S△CHF,
∴????????×5×m=????????×(3+5)×3+????????×3×(m-3),
解得m=????????????,∴F(????????????,0)
∴S△BCF=????????×BF×Cy=????????×????????????×3=????????????.
?
H
课堂总结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
情境引入
问题:你会下象棋吗?如果下一步下“马走日”,你觉得应该走到哪里呢?
新知讲解
平面直角坐标系中点的平移
1
你还记得什么叫平移吗?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行(或共线)且相等.
3.对应线段平行(或共线)且相等,对应角相等.
图形平移的性质是什么?
新知讲解
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ ,____);
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ ,____).
A1
-4
-3
3
-3
A2
y
x
新知讲解
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
-2
-5
-2
-1
A4
y
x
新知讲解
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
例1 平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2)
C.(-6,-1) D.(0,-1)
新知应用
C
点的平移变换:左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.
【解析】点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
【变式】1.若将点A向右平移5个单位长度后得到的点为(3,-3),则把点A向上平移4个单位长度后得到的点的坐标为________.
2.平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
(-2,1)
新知演练
D
跟踪练习
1.点A(-3,3)向左平移5个单位长度,得到对应点坐标是 .
(-8,3)
3.点A1(6,3)是由点A(-1,3)经过 得到的,点B(5,2)向 得到B1(7,2).
向右平移7个单位长度
右平移2个单位长度
2.将点A(3,2)向下平移2个单位长度,向右平移4个单位长度得到A1,则A1的坐标 为________.
(7,0)
4.将点P(m+1,n-2)向上平移3个单位长度,得到点Q(2,1-n),则点A(m,n)坐标为 .
(1,0)
跟踪练习
5.将点P(2m+3,m-2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,-2) B.(3,0) C.(7,0) D.(9,1)
6.在平面直角坐标中,点A(1,2)平移后的坐标是A′(-3,3),按照同样的规律平移其它点,则( )变换符合这种要求.
A.(3,2)→(4,-2)
B.(-1,0)→(-5,-4)
C.(2.5,-????????)→(-1.5,????3)
D.(1.2,5)→(-3.2,6)
?
A
C
新知讲解
平面直角坐标系中图形的平移
2
问题1:
如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),将线段AB向下平移3个单位,作出它的对应线段A′B′,并写出点A′,B′的坐标.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
x
y
B
A
新知讲解
1.作出线段两个端点平移后的对应点.
2.连接两个对应点,所得图形即为所求平移图形.
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
x
B
A
y
A′
B′
线段A′B′即为所求,
A′(1,-2),B′(4,1).
新知讲解
A
B
C
A1
B1
1.三角形ABC是怎样移动得到三角形A1B1C1?
向右平移5个单位
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
新知讲解
A
B
C
A1
B1
2.写出三角形ABC与三角形A1B1C1各点的坐标,它们有怎样的变化?
A(-1,3),B(-4,2), C(-2,1),
A1(4,3),B1(1,2),C1(3,1);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
平移后的对应点的横坐标增加了5,纵坐标不变;
新知讲解
A
B
C
A1
B1
3.如果三角形A1B1C1向下平移4个单位,得到三角形 A2B2C2,写出各点的坐标,它们有怎样的变化?
A2(4,-1),B2(1,-2),C2(3,-3);
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题2:
如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
C1
平移后的对应点的横坐标不变,纵坐标减少了4.
A2
B2
C2
新知讲解
A
B
C
A1
B1
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
-2
-3
-4
-6
-5
1
y
问题3:
三角形 ABC能否在坐标平面内直接平移后得到三角形 A2B2C2 ?
C1
一般地,图形经过两次平移后得到的图形,可以通过原来的图形作一次平移得到.
A2
B2
C2
通过对以上问题的探讨,你能说出图形平移的规律吗?
新知讲解
向右平移a个单位
原图形上的点P(x,y)
向左平移a个单位
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
向下平移b个单位
P3(x,y+b)
P4(x,y-b)
图形的平移规律
图形的平移与图形上某一点的平移规律是一致的,因此,图形的平移问题可以转化为某一点的平移问题.
新知讲解
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
(x+a,y+b)
(x+a,y-b)
(x-a,y+b)
(x-a,y-b)
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
图形的平移方向和平移距离
图形上对应点的坐标
例2 如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
新知应用
1
y
O
1
A
B
C
A1
B1
C1
解:三角形A1B1C1如图所示,
各点的坐标分别为:A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
x
(1)请画出上述平移后的三角形A1B1C1,并写出点A、C、
A1、C1的坐标;
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
解:连接AA1,CC1,
新知应用
1
y
O
1
A
B
C
A1
B1
C1
x
=????????×2×7=7=
?
【变式】1.将一个三角形的三个顶点分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别为( )
A.(6,0), (3,2), (8,-6)
B.(-1,-5), (2,-7), (3,-1)
C.(1,5), (2,-7), (-3,1)
D.(-1,5), (2,-7), (-3,1)
A
新知演练
【变式】2.如图,△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出△A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
解:(1)△A1B1C1是由△ABC向左平移3个单位,再向上平移1个单位所得,则
A1(-1,2),B1(2,4),C1 (0,5);
(2)如图,△ABC的面积
=3×3-????????×1×3-????????×1×2-????????×2×3
=3.5
?
新知演练
跟踪练习
1.在6×6方格中,将图①中的图形甲平移后位置如图②所示,则图形甲的平移方法正确的是( )
A.先向左平移1格,再向下平移2格
B.先向右平移3格,再向下平移2格
C.先向右平移1格,再向下平移3格
D.先向右平移2格,再向下平移3格
C
跟踪练习
2.线段CD是由线段AB平移得到的.其中点A(-1,4)的对应点为C(4,4),则点B(-4,-1)的对应点D的坐标为________.
(1,-1)
3.(1)已知线段MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为______________________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为_________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
4.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1. 求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);
B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
A
跟踪练习
拓展练习
1.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
解:(1)如图所示:
A′(0,4)、B′(-1,1)、C′(3,1);
(2)S△ABC=????????×(3+1)×3=6
?
A′
B′
C′
拓展练习
1.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
解:设点P坐标为(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得????????×4×|y+2|=6,
解得y=1或y=-5,
所以点P的坐标为(0,1)或(0,-5).
?
拓展练习
2.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
(2)向右平移5个单位,再向上平移3个单位.
拓展练习
2.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(3)求△BCF的面积.
解:作CH⊥OF于H.设F(m,0),
∵S△AOF=S四边形AOHC+S△CHF,
∴????????×5×m=????????×(3+5)×3+????????×3×(m-3),
解得m=????????????,∴F(????????????,0)
∴S△BCF=????????×BF×Cy=????????×????????????×3=????????????.
?
H
课堂总结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
