山东省德州市平原江山国际学校2020-2021学年九年级下学期开学摸底考试数学试题 word解析版
文档属性
| 名称 | 山东省德州市平原江山国际学校2020-2021学年九年级下学期开学摸底考试数学试题 word解析版 |
|
|
| 格式 | doc | ||
| 文件大小 | 624.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览

文档简介
山东省德州市平原江山国际学校2020-2021学年九年级下学期开学摸底考试数学试题
一.选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号写在答题卡上)
1.2020的倒数的相反数是( )
A.﹣2020 B.﹣ C. D.2020
2.如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
A. B. C. D.
3.下列计算结果正确的是( )
A.(﹣a3)2=a9 B.a2?a3=a6
C.﹣22=﹣2 D.=1
4.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b+2019的值是( )
A.2023 B.2021 C.2020 D.2019
5.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
6.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则函数中k的取值范围是( )
A.k≥﹣2 B.k≤﹣2 C.k≥2 D.k≤2
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为( )
A.4 B.3 C.2 D.
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,2+) D.(﹣1,2+)
9.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )
A. B.
C. D.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
11.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,) C.(2,) D.(,)
12.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而增大.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
二.填空题(本大题共6个题每题4分,共24分,把答案填在答题卡的相应位置上)
13.从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是
14.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
15.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 .
16.把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是 cm2.
17.若满足不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,则a+b的值为
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
三.解答题(共78分.解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
19.用适当的方法解下列方程:
(1)x2﹣4x﹣5=0;
(2)(x﹣1)2=2x﹣2.
20.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2;
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标;
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
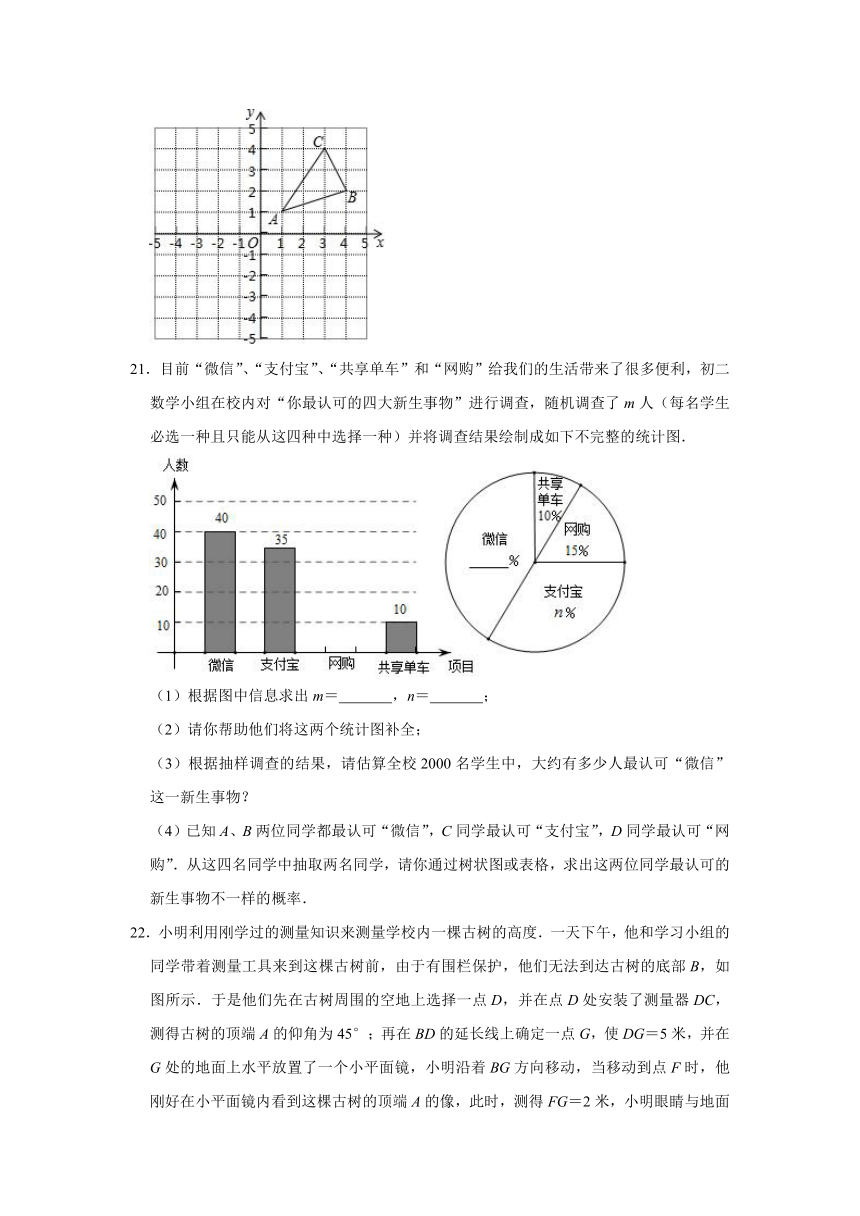
21.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”.从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
22.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
23.某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式;
(2)求W与x的函数关系式(不必写出x的取值范围)
(3)若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?
24.如图,在△ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6,求此时DE的长.
25.如图,二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.
参考答案
一.选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号写在答题卡上)
1.2020的倒数的相反数是( )
A.﹣2020 B.﹣ C. D.2020
【分析】先表示出2020的倒数,再利用相反数的概念求解可得.
【解答】解:2020的倒数为,
所以2020的倒数的相反数是﹣,
故选:B.
2.如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
A. B. C. D.
【分析】根据从上边看得到的图形是俯视图,可得答案.
【解答】解:它的俯视图为
故选:A.
3.下列计算结果正确的是( )
A.(﹣a3)2=a9 B.a2?a3=a6
C.﹣22=﹣2 D.=1
【分析】利用幂的乘方与积的乘方,同底数幂的乘法,零指数幂及负整数指数幂的法则判定即可.
【解答】解:A、(﹣a3)2=a6,故本选项不正确,
B、a2?a3=a5,故本选项不正确,
C、﹣22=﹣2,故本选项正确,
D、cos60°﹣=0,故本选项不正确,
故选:C.
4.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b+2019的值是( )
A.2023 B.2021 C.2020 D.2019
【分析】根据题意可知b=3﹣b2,a+b=﹣1,ab=3,所求式子化为a2﹣b+2019=a2﹣3+b2+2019=(a+b)2﹣2ab+2016即可求解;
【解答】解:a,b是方程x2+x﹣3=0的两个实数根,
∴b=3﹣b2,a+b=﹣1,ab=﹣3,
∴a2﹣b+2019=a2﹣3+b2+2019=(a+b)2﹣2ab+2016=1+6+2016=2023;
故选:A.
5.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
【分析】利用OB=DE,OB=OD得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可.
【解答】解:连结OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
6.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则函数中k的取值范围是( )
A.k≥﹣2 B.k≤﹣2 C.k≥2 D.k≤2
【分析】先利用二次函数的性质求出抛物线的对称轴为直线x=﹣k,则当x>﹣k时,y的值随x值的增大而减小,由于x>﹣2时,y的值随x值的增大而减小,于是得到﹣k≤﹣2,再解不等式即可.
【解答】解:抛物线的对称轴为直线x=﹣k,
因为a=﹣1<0,
所以抛物线开口向下,
所以当x>﹣k时,y的值随x值的增大而减小,
而x>﹣2时,y的值随x值的增大而减小,
所以﹣k≤﹣2,
所以k≥2.
故选:C.
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为( )
A.4 B.3 C.2 D.
【分析】先求出点A,B的坐标,再根据AC∥BD∥y轴,确定点C,点D的坐标,求出AC,BD,最后根据,△OAC与△ABD的面积之和为,即可解答.
【解答】解:∵点A,B在反比例函数y=(x>0)的图象上,点A,B的横坐标分别为1,2,
∴点A的坐标为(1,1),点B的坐标为(2,),
∵AC∥BD∥y轴,
∴点C,D的横坐标分别为1,2,
∵点C,D在反比例函数y=(k>0)的图象上,
∴点C的坐标为(1,k),点D的坐标为(2,),
∴AC=k﹣1,BD=,
∴S△OAC=(k﹣1)×1=,S△ABD=?×(2﹣1)=,
∵△OAC与△ABD的面积之和为,
∴,
解得:k=3.
故选:B.
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,2+) D.(﹣1,2+)
【分析】如图,过点B′作B′H⊥y轴于H.解直角三角形求出OH,B′H即可.
【解答】解:如图,过点B′作B′H⊥y轴于H.
在Rt△A′B′H中,∵A′B′=2,∠B′A′H=60°,
∴A′H=A′B′cos60°=1,B′H=A′B′sin60°=,
∴OH=2+1=3,
∴B′(﹣,3),
故选:A.
9.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )
A. B.
C. D.
【分析】本题主要应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
【解答】解:已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.
故选:B.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
【分析】设合伙人数为x人,根据羊的总价钱不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:设合伙人数为x人,
依题意,得:5x+45=7x+3.
故选:B.
11.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,) C.(2,) D.(,)
【分析】过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2,故OD=4﹣2,即B′点的坐标为(2,).
【解答】解:过点B′作B′D⊥OC
∵∠CPB=60°,CB′=OC=OA=4
∴∠B′CD=30°,B′D=2
根据勾股定理得DC=2
∴OD=4﹣2,即B′点的坐标为(2,)
故选:C.
12.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而增大.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:①由图象可知:a>0,c<0,
∵﹣=1,
∴b=﹣2a<0,
∴abc>0,故①错误;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,故④正确;
⑤当x=1时,y取到值最小,此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,
故a+b≤am2+bm,即a+b≤m(am+b),故⑤正确,
⑥当x<﹣1时,y随x的增大而减小,故⑥错误,
故选:A.
二.填空题(本大题共6个题每题4分,共24分,把答案填在答题卡的相应位置上)
13.从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是
【分析】画树状图展示所有6种等可能的结果数,再找出组成的两位数是4的倍数的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有6种等可能的结果数,其中组成的两位数是4的倍数的结果数为2,
所以组成的两位数是4的倍数的概率==.
故答案为.
14.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
【分析】根据圆周角定理得到∠ADC=∠B,因而sinB=sin∠ADC=.
【解答】解:∵AD是直径,
∴∠ACD=90°.
∵AD=3,AC=2,
∴sinADC==.
∵∠ADC=∠B,
∴sinB=.
故答案为.
15.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 2 .
【分析】作OH⊥CD于H,连接OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【解答】解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
16.把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是 27 cm2.
【分析】本题考查直角三角形的性质和勾股定理,利用直角三角形的性质和勾股定理解答.
【解答】解:∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°,
∴=,cos∠ABC=cos30°==,
∴AB=BE=2AC=2DE=2×6=12,BC=×AB=×12=6,
∴BD=6,
过D作DF⊥BE,在Rt△BDF中,∠DBE=30°,
∴==,DF=3,
∴S△BCD=BC?DF=×6×3=27cm2.
故答案为:27.
17.若满足不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,则a+b的值为 ﹣2
【分析】根据不等式﹣3<1﹣2x<的可以求得x的取值范围,从而可以得到a、b的值,进而求得a+b的值.
【解答】解:∵﹣3<1﹣2x<,
解得,﹣<x<2,
∵不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,
∴a=1,b=﹣3,
∴a+b=1+(﹣3)=﹣2,
故答案为:﹣2.
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (2n,1) (用n表示).
【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可.
【解答】解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
三.解答题(共78分.解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
19.用适当的方法解下列方程:
(1)x2﹣4x﹣5=0;
(2)(x﹣1)2=2x﹣2.
【分析】利用因式分解法求解即可.
【解答】解:(1)∵x2﹣4x﹣5=0,
∴(x﹣5)(x+1)=0,
则x﹣5=0或x+1=0,
解得x1=5,x2=﹣1;
(2)∵(x﹣1)2=2x﹣2,
∴(x﹣1)2﹣2(x﹣1)=0,
则(x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
解得x1=1,x2=3.
20.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2;
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标;
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出A,B,C关于点(1,0)的对称点A2,B2,C2即可.
(3)连接A1A2,B1B2交于点M,点M即为所求.
(4)连接BA2交x轴于点P,点P即为所求.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,点M即为所求,点M的坐标(﹣1,0).
(4)如图,点P即为所求,点P的坐标(2,0).
21.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出m= 100 ,n= 35 ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”.从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
【分析】(1)由共享单车人数及其百分比求得总人数m,用支付宝人数除以总人数可得其百分比n的值;
(2)总人数乘以网购人数的百分比可得其人数,用微信人数除以总人数求得其百分比即可补全两个图形;
(3)总人数乘以样本中微信人数所占百分比可得答案;
(4)列表得出所有等可能结果,从中找到这两位同学最认可的新生事物不一样的结果数,根据概率公式计算可得.
【解答】解:(1)∵被调查的总人数m=10÷10%=100人,
∴支付宝的人数所占百分比n%=×100%=35%,即n=35,
故答案为:100、35;
(2)网购人数为100×15%=15人,微信对应的百分比为×100%=40%,
补全图形如下:
(3)估算全校2000名学生中,最认可“微信”这一新生事物的人数为2000×40%=800(人);
答:大约有800人最认可“微信”这一新生事物.
(4)列表如下:
共有12种等可能情况,这两位同学最认可的新生事物不一样的有10种;
所以这两位同学最认可的新生事物不一样的概率为P==.
22.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
【分析】过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5米,解Rt△ACH,得出AH=CH=BD,那么AB=AH+BH=BD+0.5,再证明△EFG∽△ABG,根据相似三角形对应边成比例求出BD=17.5米,进而求出AB即可.
【解答】解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=0.5米.
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由反射角等于入射角得∠EGF=∠AGB,
∴△EFG∽△ABG(AA),
∴=即=,
解得BD=17.5,
∴AB=17.5+0.5=18(m).
∴这棵古树的高AB为18m.
23.某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式;
(2)求W与x的函数关系式(不必写出x的取值范围)
(3)若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?
【分析】(1)根据销售量等于原销售量加上多卖出的量即可求解;
(2)根据每天获得利润等于单件利润乘以销售量即可求解;
(3)根据二次函数的性质即可求解.
【解答】解:(1)根据题意,得
y=30+5x.
答:y与x的函数关系式y=30+5x.
(2)根据题意,得
W=(20﹣10﹣x)(30+5x)
=﹣5x2+20x+300.
答:W与x的函数关系式为W=﹣5x2+20x+300.
(3)W=﹣5x2+20x+300
=﹣5(x﹣2)2+320
∵﹣5<0,对称轴x=2,
∵x不低于4元即x≥4,
在对称轴右侧,W随x的增大而减小,
∴x=4时,W有最大值为300,
答:降价4元(x不低于4元)时,销售这种商品每天获得的利润最大为300元.
24.如图,在△ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6,求此时DE的长.
【分析】(1)连接OD、BD,求出BD⊥AC,可得AD=DC,根据三角形的中位线得出OD∥BC,推出OD⊥DE,根据切线的判定推出即可;
(2)根据题意求得AD,根据勾股定理求得BD,然后证得△CDE∽△ABD,根据相似三角形的性质即可求得DE.
【解答】(1)证明:连接OD、BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴D为AC中点,
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O的切线;
(2)由(1)知BD是AC的中线,
∴AD=CD==3,
∵⊙O的半径为5,
∴AB=10,
∴BD===,
∵AB=BC,
∴∠A=∠C,
∵∠ADB=∠CED=90°,
∴△CDE∽△ABD,
∴,即=,
∴DE=3.
25.如图,二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.
【分析】(1)由题意得出方程组,求出二次函数的解析式为y=﹣x2+3x+4,则C(0,4),由待定系数法求出BC所在直线的表达式即可
(2)证DE∥PF,只要DE=PF,四边形DEFP即为平行四边形,由二次函数解析式求出点D的坐标,由直线BC的解析式求出点E的坐标,则DE=,设点P的横坐标为t,则P的坐标为:(t,﹣t2+3t+4),F的坐标为:(t,﹣t+4),由DE=PF得出方程,解方程进而得出答案;
(3)由平行线的性质得出∠CED=∠CFP,当∠PCF=∠CDE时,△PCF∽△CDE,则=,得出方程,解方程即可.
【解答】解:(1)将点A(﹣1,0),B(4,0),代入y=ax2+bx+4,
得:,
解得:,
∴二次函数的表达式为:y=﹣x2+3x+4,
当x=0时,y=4,
∴C(0,4),
设BC所在直线的表达式为:y=mx+n,
将C(0,4)、B(4,0)代入y=mx+n,
得:,
解得:,
∴BC所在直线的表达式为:y=﹣x+4;
(2)∵DE⊥x轴,PF⊥x轴,
∴DE∥PF,
只要DE=PF,四边形DEFP即为平行四边形,
∵y=﹣x2+3x+4=﹣(x﹣)2+,
∴点D的坐标为:(,),
将x=代入y=﹣x+4,即y=﹣+4=,
∴点E的坐标为:(,),
∴DE=﹣=,
设点P的横坐标为t,
则P的坐标为:(t,﹣t2+3t+4),F的坐标为:(t,﹣t+4),
∴PF=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t,
由DE=PF得:﹣t2+4t=,
解得:t1=(不合题意舍去),t2=,
当t=时,﹣t2+3t+4=﹣()2+3×+4=,
∴点P的坐标为(,);
(3)存在,理由如下:
如图2所示:
由(2)得:PF∥DE,
∴∠CED=∠CFP,
又∵∠PCF与∠DCE有共同的顶点C,且∠PCF在∠DCE的内部,
∴∠PCF≠∠DCE,
∴只有∠PCF=∠CDE时,△PCF∽△CDE,
∴=,
∵C(0,4)、E(,),
∴CE==,
由(2)得:DE=,PF=﹣t2+4t,F的坐标为:(t,﹣t+4),
∴CF==t,
∴=,
∵t≠0,
∴(﹣t+4)=3,
解得:t=,
当t=时,﹣t2+3t+4=﹣()2+3×+4=,
∴点P的坐标为:(,).
一.选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号写在答题卡上)
1.2020的倒数的相反数是( )
A.﹣2020 B.﹣ C. D.2020
2.如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
A. B. C. D.
3.下列计算结果正确的是( )
A.(﹣a3)2=a9 B.a2?a3=a6
C.﹣22=﹣2 D.=1
4.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b+2019的值是( )
A.2023 B.2021 C.2020 D.2019
5.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
6.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则函数中k的取值范围是( )
A.k≥﹣2 B.k≤﹣2 C.k≥2 D.k≤2
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为( )
A.4 B.3 C.2 D.
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,2+) D.(﹣1,2+)
9.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )
A. B.
C. D.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
11.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,) C.(2,) D.(,)
12.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而增大.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
二.填空题(本大题共6个题每题4分,共24分,把答案填在答题卡的相应位置上)
13.从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是
14.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
15.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 .
16.把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是 cm2.
17.若满足不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,则a+b的值为
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).
三.解答题(共78分.解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
19.用适当的方法解下列方程:
(1)x2﹣4x﹣5=0;
(2)(x﹣1)2=2x﹣2.
20.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2;
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标;
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
21.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”.从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
22.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
23.某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式;
(2)求W与x的函数关系式(不必写出x的取值范围)
(3)若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?
24.如图,在△ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6,求此时DE的长.
25.如图,二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.
参考答案
一.选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号写在答题卡上)
1.2020的倒数的相反数是( )
A.﹣2020 B.﹣ C. D.2020
【分析】先表示出2020的倒数,再利用相反数的概念求解可得.
【解答】解:2020的倒数为,
所以2020的倒数的相反数是﹣,
故选:B.
2.如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )
A. B. C. D.
【分析】根据从上边看得到的图形是俯视图,可得答案.
【解答】解:它的俯视图为
故选:A.
3.下列计算结果正确的是( )
A.(﹣a3)2=a9 B.a2?a3=a6
C.﹣22=﹣2 D.=1
【分析】利用幂的乘方与积的乘方,同底数幂的乘法,零指数幂及负整数指数幂的法则判定即可.
【解答】解:A、(﹣a3)2=a6,故本选项不正确,
B、a2?a3=a5,故本选项不正确,
C、﹣22=﹣2,故本选项正确,
D、cos60°﹣=0,故本选项不正确,
故选:C.
4.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b+2019的值是( )
A.2023 B.2021 C.2020 D.2019
【分析】根据题意可知b=3﹣b2,a+b=﹣1,ab=3,所求式子化为a2﹣b+2019=a2﹣3+b2+2019=(a+b)2﹣2ab+2016即可求解;
【解答】解:a,b是方程x2+x﹣3=0的两个实数根,
∴b=3﹣b2,a+b=﹣1,ab=﹣3,
∴a2﹣b+2019=a2﹣3+b2+2019=(a+b)2﹣2ab+2016=1+6+2016=2023;
故选:A.
5.如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于( )
A.42° B.28° C.21° D.20°
【分析】利用OB=DE,OB=OD得到DO=DE,则∠E=∠DOE,根据三角形外角性质得∠1=∠DOE+∠E,所以∠1=2∠E,同理得到∠AOC=∠C+∠E=3∠E,然后利用∠E=∠AOC进行计算即可.
【解答】解:连结OD,如图,
∵OB=DE,OB=OD,
∴DO=DE,
∴∠E=∠DOE,
∵∠1=∠DOE+∠E,
∴∠1=2∠E,
而OC=OD,
∴∠C=∠1,
∴∠C=2∠E,
∴∠AOC=∠C+∠E=3∠E,
∴∠E=∠AOC=×84°=28°.
故选:B.
6.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则函数中k的取值范围是( )
A.k≥﹣2 B.k≤﹣2 C.k≥2 D.k≤2
【分析】先利用二次函数的性质求出抛物线的对称轴为直线x=﹣k,则当x>﹣k时,y的值随x值的增大而减小,由于x>﹣2时,y的值随x值的增大而减小,于是得到﹣k≤﹣2,再解不等式即可.
【解答】解:抛物线的对称轴为直线x=﹣k,
因为a=﹣1<0,
所以抛物线开口向下,
所以当x>﹣k时,y的值随x值的增大而减小,
而x>﹣2时,y的值随x值的增大而减小,
所以﹣k≤﹣2,
所以k≥2.
故选:C.
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为( )
A.4 B.3 C.2 D.
【分析】先求出点A,B的坐标,再根据AC∥BD∥y轴,确定点C,点D的坐标,求出AC,BD,最后根据,△OAC与△ABD的面积之和为,即可解答.
【解答】解:∵点A,B在反比例函数y=(x>0)的图象上,点A,B的横坐标分别为1,2,
∴点A的坐标为(1,1),点B的坐标为(2,),
∵AC∥BD∥y轴,
∴点C,D的横坐标分别为1,2,
∵点C,D在反比例函数y=(k>0)的图象上,
∴点C的坐标为(1,k),点D的坐标为(2,),
∴AC=k﹣1,BD=,
∴S△OAC=(k﹣1)×1=,S△ABD=?×(2﹣1)=,
∵△OAC与△ABD的面积之和为,
∴,
解得:k=3.
故选:B.
8.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,2+) D.(﹣1,2+)
【分析】如图,过点B′作B′H⊥y轴于H.解直角三角形求出OH,B′H即可.
【解答】解:如图,过点B′作B′H⊥y轴于H.
在Rt△A′B′H中,∵A′B′=2,∠B′A′H=60°,
∴A′H=A′B′cos60°=1,B′H=A′B′sin60°=,
∴OH=2+1=3,
∴B′(﹣,3),
故选:A.
9.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )
A. B.
C. D.
【分析】本题主要应用两三角形相似判定定理,三边对应成比例,分别对各选项进行分析即可得出答案.
【解答】解:已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.
故选:B.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
【分析】设合伙人数为x人,根据羊的总价钱不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:设合伙人数为x人,
依题意,得:5x+45=7x+3.
故选:B.
11.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,) C.(2,) D.(,)
【分析】过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2,故OD=4﹣2,即B′点的坐标为(2,).
【解答】解:过点B′作B′D⊥OC
∵∠CPB=60°,CB′=OC=OA=4
∴∠B′CD=30°,B′D=2
根据勾股定理得DC=2
∴OD=4﹣2,即B′点的坐标为(2,)
故选:C.
12.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数),⑥当x<﹣1时,y随x的增大而增大.其中结论正确的个数为( )
A.3 B.4 C.5 D.6
【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:①由图象可知:a>0,c<0,
∵﹣=1,
∴b=﹣2a<0,
∴abc>0,故①错误;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,故④正确;
⑤当x=1时,y取到值最小,此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,
故a+b≤am2+bm,即a+b≤m(am+b),故⑤正确,
⑥当x<﹣1时,y随x的增大而减小,故⑥错误,
故选:A.
二.填空题(本大题共6个题每题4分,共24分,把答案填在答题卡的相应位置上)
13.从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是
【分析】画树状图展示所有6种等可能的结果数,再找出组成的两位数是4的倍数的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有6种等可能的结果数,其中组成的两位数是4的倍数的结果数为2,
所以组成的两位数是4的倍数的概率==.
故答案为.
14.如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值是 .
【分析】根据圆周角定理得到∠ADC=∠B,因而sinB=sin∠ADC=.
【解答】解:∵AD是直径,
∴∠ACD=90°.
∵AD=3,AC=2,
∴sinADC==.
∵∠ADC=∠B,
∴sinB=.
故答案为.
15.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为 2 .
【分析】作OH⊥CD于H,连接OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA﹣AP=2,接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【解答】解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
16.把两块含有30°的相同的直角三角尺按如图所示摆放,使点C、B、E在同一直线上,连接CD,若AC=6cm,则△BCD的面积是 27 cm2.
【分析】本题考查直角三角形的性质和勾股定理,利用直角三角形的性质和勾股定理解答.
【解答】解:∵两块三角尺是有30°的相同的直角三角尺,∠ABC=∠EBD=30°,
∴=,cos∠ABC=cos30°==,
∴AB=BE=2AC=2DE=2×6=12,BC=×AB=×12=6,
∴BD=6,
过D作DF⊥BE,在Rt△BDF中,∠DBE=30°,
∴==,DF=3,
∴S△BCD=BC?DF=×6×3=27cm2.
故答案为:27.
17.若满足不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,则a+b的值为 ﹣2
【分析】根据不等式﹣3<1﹣2x<的可以求得x的取值范围,从而可以得到a、b的值,进而求得a+b的值.
【解答】解:∵﹣3<1﹣2x<,
解得,﹣<x<2,
∵不等式﹣3<1﹣2x<的最大整数解为a,最小整数解为b,
∴a=1,b=﹣3,
∴a+b=1+(﹣3)=﹣2,
故答案为:﹣2.
18.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (2n,1) (用n表示).
【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可.
【解答】解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
三.解答题(共78分.解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
19.用适当的方法解下列方程:
(1)x2﹣4x﹣5=0;
(2)(x﹣1)2=2x﹣2.
【分析】利用因式分解法求解即可.
【解答】解:(1)∵x2﹣4x﹣5=0,
∴(x﹣5)(x+1)=0,
则x﹣5=0或x+1=0,
解得x1=5,x2=﹣1;
(2)∵(x﹣1)2=2x﹣2,
∴(x﹣1)2﹣2(x﹣1)=0,
则(x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
解得x1=1,x2=3.
20.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2;
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标;
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出A,B,C关于点(1,0)的对称点A2,B2,C2即可.
(3)连接A1A2,B1B2交于点M,点M即为所求.
(4)连接BA2交x轴于点P,点P即为所求.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,点M即为所求,点M的坐标(﹣1,0).
(4)如图,点P即为所求,点P的坐标(2,0).
21.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出m= 100 ,n= 35 ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”.从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
【分析】(1)由共享单车人数及其百分比求得总人数m,用支付宝人数除以总人数可得其百分比n的值;
(2)总人数乘以网购人数的百分比可得其人数,用微信人数除以总人数求得其百分比即可补全两个图形;
(3)总人数乘以样本中微信人数所占百分比可得答案;
(4)列表得出所有等可能结果,从中找到这两位同学最认可的新生事物不一样的结果数,根据概率公式计算可得.
【解答】解:(1)∵被调查的总人数m=10÷10%=100人,
∴支付宝的人数所占百分比n%=×100%=35%,即n=35,
故答案为:100、35;
(2)网购人数为100×15%=15人,微信对应的百分比为×100%=40%,
补全图形如下:
(3)估算全校2000名学生中,最认可“微信”这一新生事物的人数为2000×40%=800(人);
答:大约有800人最认可“微信”这一新生事物.
(4)列表如下:
共有12种等可能情况,这两位同学最认可的新生事物不一样的有10种;
所以这两位同学最认可的新生事物不一样的概率为P==.
22.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
【分析】过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5米,解Rt△ACH,得出AH=CH=BD,那么AB=AH+BH=BD+0.5,再证明△EFG∽△ABG,根据相似三角形对应边成比例求出BD=17.5米,进而求出AB即可.
【解答】解:如图,过点C作CH⊥AB于点H,
则CH=BD,BH=CD=0.5米.
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由反射角等于入射角得∠EGF=∠AGB,
∴△EFG∽△ABG(AA),
∴=即=,
解得BD=17.5,
∴AB=17.5+0.5=18(m).
∴这棵古树的高AB为18m.
23.某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数关系式;
(2)求W与x的函数关系式(不必写出x的取值范围)
(3)若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?
【分析】(1)根据销售量等于原销售量加上多卖出的量即可求解;
(2)根据每天获得利润等于单件利润乘以销售量即可求解;
(3)根据二次函数的性质即可求解.
【解答】解:(1)根据题意,得
y=30+5x.
答:y与x的函数关系式y=30+5x.
(2)根据题意,得
W=(20﹣10﹣x)(30+5x)
=﹣5x2+20x+300.
答:W与x的函数关系式为W=﹣5x2+20x+300.
(3)W=﹣5x2+20x+300
=﹣5(x﹣2)2+320
∵﹣5<0,对称轴x=2,
∵x不低于4元即x≥4,
在对称轴右侧,W随x的增大而减小,
∴x=4时,W有最大值为300,
答:降价4元(x不低于4元)时,销售这种商品每天获得的利润最大为300元.
24.如图,在△ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6,求此时DE的长.
【分析】(1)连接OD、BD,求出BD⊥AC,可得AD=DC,根据三角形的中位线得出OD∥BC,推出OD⊥DE,根据切线的判定推出即可;
(2)根据题意求得AD,根据勾股定理求得BD,然后证得△CDE∽△ABD,根据相似三角形的性质即可求得DE.
【解答】(1)证明:连接OD、BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴D为AC中点,
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O的切线;
(2)由(1)知BD是AC的中线,
∴AD=CD==3,
∵⊙O的半径为5,
∴AB=10,
∴BD===,
∵AB=BC,
∴∠A=∠C,
∵∠ADB=∠CED=90°,
∴△CDE∽△ABD,
∴,即=,
∴DE=3.
25.如图,二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.
【分析】(1)由题意得出方程组,求出二次函数的解析式为y=﹣x2+3x+4,则C(0,4),由待定系数法求出BC所在直线的表达式即可
(2)证DE∥PF,只要DE=PF,四边形DEFP即为平行四边形,由二次函数解析式求出点D的坐标,由直线BC的解析式求出点E的坐标,则DE=,设点P的横坐标为t,则P的坐标为:(t,﹣t2+3t+4),F的坐标为:(t,﹣t+4),由DE=PF得出方程,解方程进而得出答案;
(3)由平行线的性质得出∠CED=∠CFP,当∠PCF=∠CDE时,△PCF∽△CDE,则=,得出方程,解方程即可.
【解答】解:(1)将点A(﹣1,0),B(4,0),代入y=ax2+bx+4,
得:,
解得:,
∴二次函数的表达式为:y=﹣x2+3x+4,
当x=0时,y=4,
∴C(0,4),
设BC所在直线的表达式为:y=mx+n,
将C(0,4)、B(4,0)代入y=mx+n,
得:,
解得:,
∴BC所在直线的表达式为:y=﹣x+4;
(2)∵DE⊥x轴,PF⊥x轴,
∴DE∥PF,
只要DE=PF,四边形DEFP即为平行四边形,
∵y=﹣x2+3x+4=﹣(x﹣)2+,
∴点D的坐标为:(,),
将x=代入y=﹣x+4,即y=﹣+4=,
∴点E的坐标为:(,),
∴DE=﹣=,
设点P的横坐标为t,
则P的坐标为:(t,﹣t2+3t+4),F的坐标为:(t,﹣t+4),
∴PF=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t,
由DE=PF得:﹣t2+4t=,
解得:t1=(不合题意舍去),t2=,
当t=时,﹣t2+3t+4=﹣()2+3×+4=,
∴点P的坐标为(,);
(3)存在,理由如下:
如图2所示:
由(2)得:PF∥DE,
∴∠CED=∠CFP,
又∵∠PCF与∠DCE有共同的顶点C,且∠PCF在∠DCE的内部,
∴∠PCF≠∠DCE,
∴只有∠PCF=∠CDE时,△PCF∽△CDE,
∴=,
∵C(0,4)、E(,),
∴CE==,
由(2)得:DE=,PF=﹣t2+4t,F的坐标为:(t,﹣t+4),
∴CF==t,
∴=,
∵t≠0,
∴(﹣t+4)=3,
解得:t=,
当t=时,﹣t2+3t+4=﹣()2+3×+4=,
∴点P的坐标为:(,).
同课章节目录
