2020-2021学年北师大版九年级数学下册第三章圆单元测试题(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第三章圆单元测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 402.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:04:21 | ||
图片预览

文档简介
2020-2021学年北师大版九年级数学下册第三章
圆
单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.下列说法正确的是(
)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(
)
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(
)
A.70°
B.60°
C.50°
D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(
)
A.r=R
B.r=R
C.r=R
D.r=R
5.如图,在平面直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为(
)
A.12
B.10
C.14
D.15
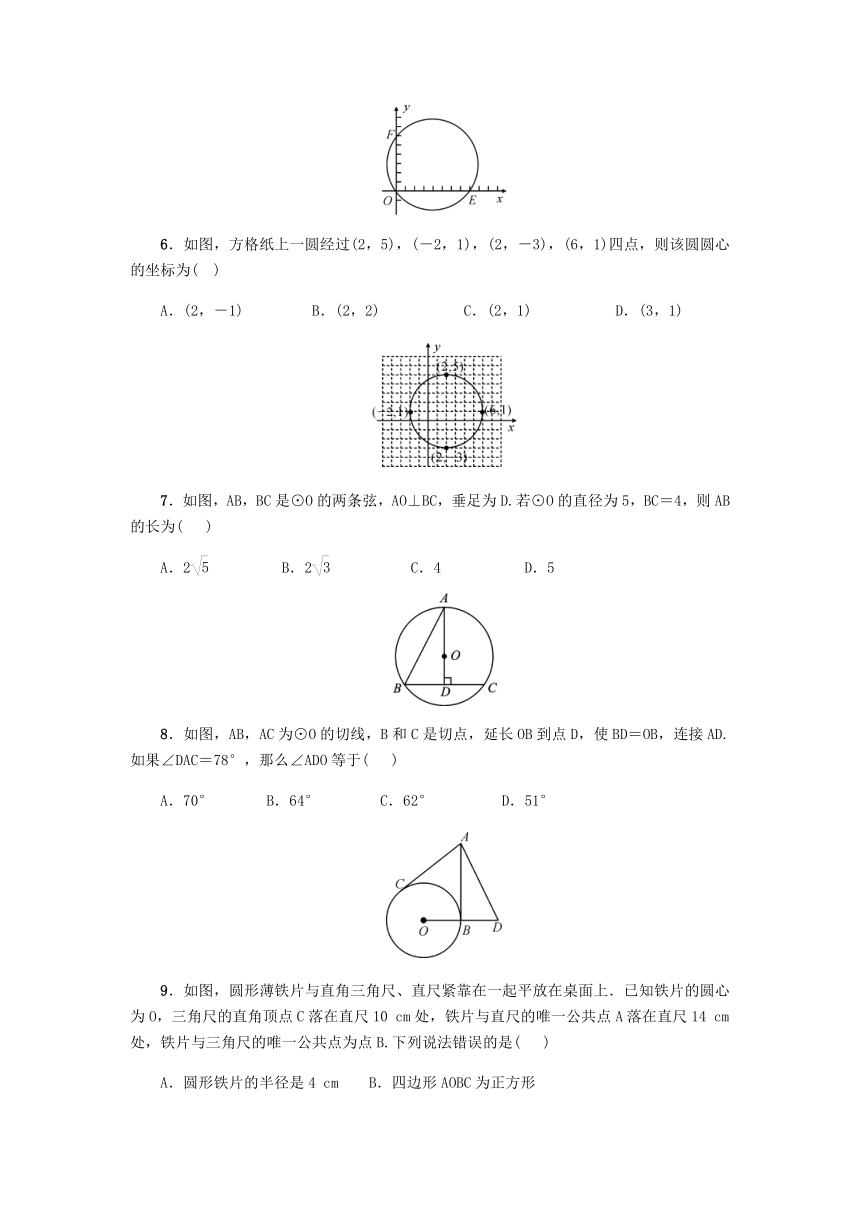
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(
)
A.(2,-1)
B.(2,2)
C.(2,1)
D.(3,1)
7.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D.若⊙O的直径为5,BC=4,则AB的长为(
)
A.2
B.2
C.4
D.5
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于(
)
A.70°
B.64°
C.62°
D.51°
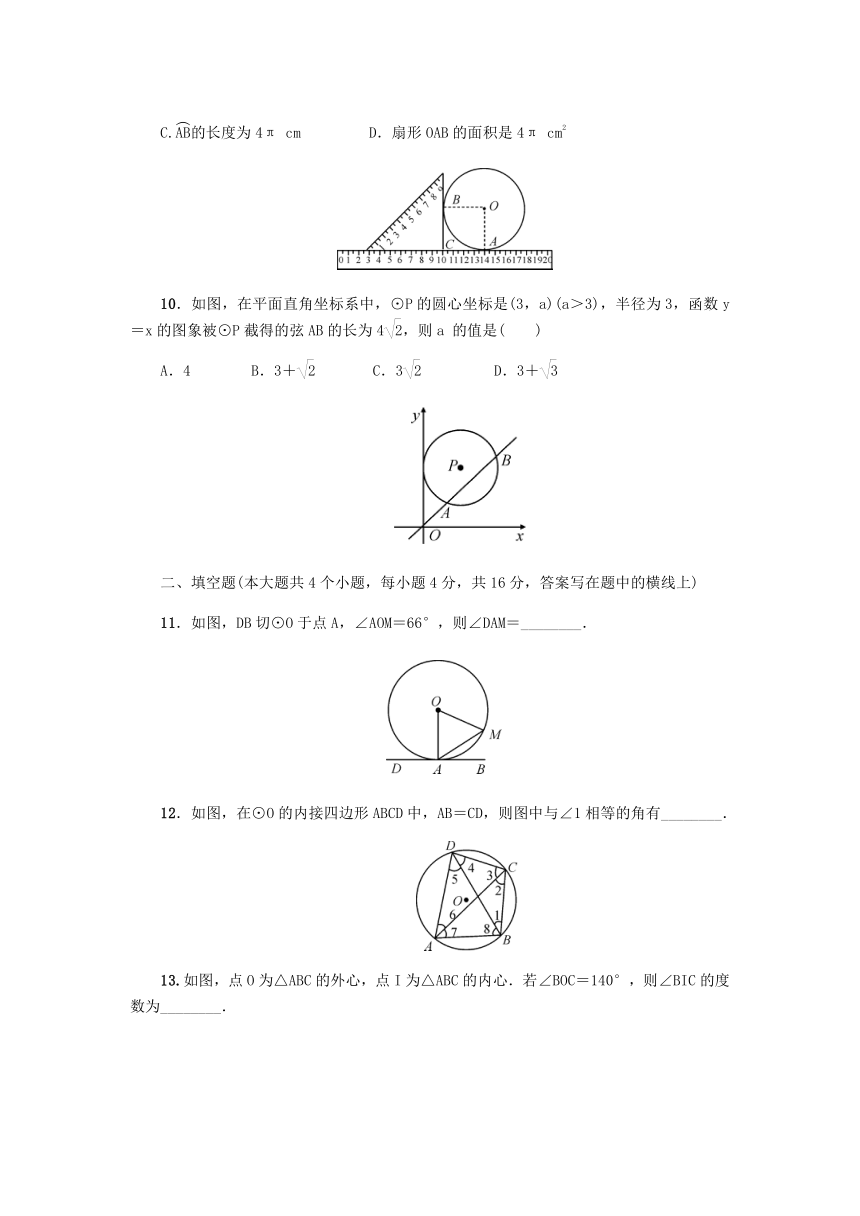
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10
cm处,铁片与直尺的唯一公共点A落在直尺14
cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(
)
A.圆形铁片的半径是4
cm
B.四边形AOBC为正方形
C.的长度为4π
cm
D.扇形OAB的面积是4π
cm2
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a
的值是(
)
A.4
B.3+
C.3
D.3+
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=________.
12.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有________.
13.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为________.
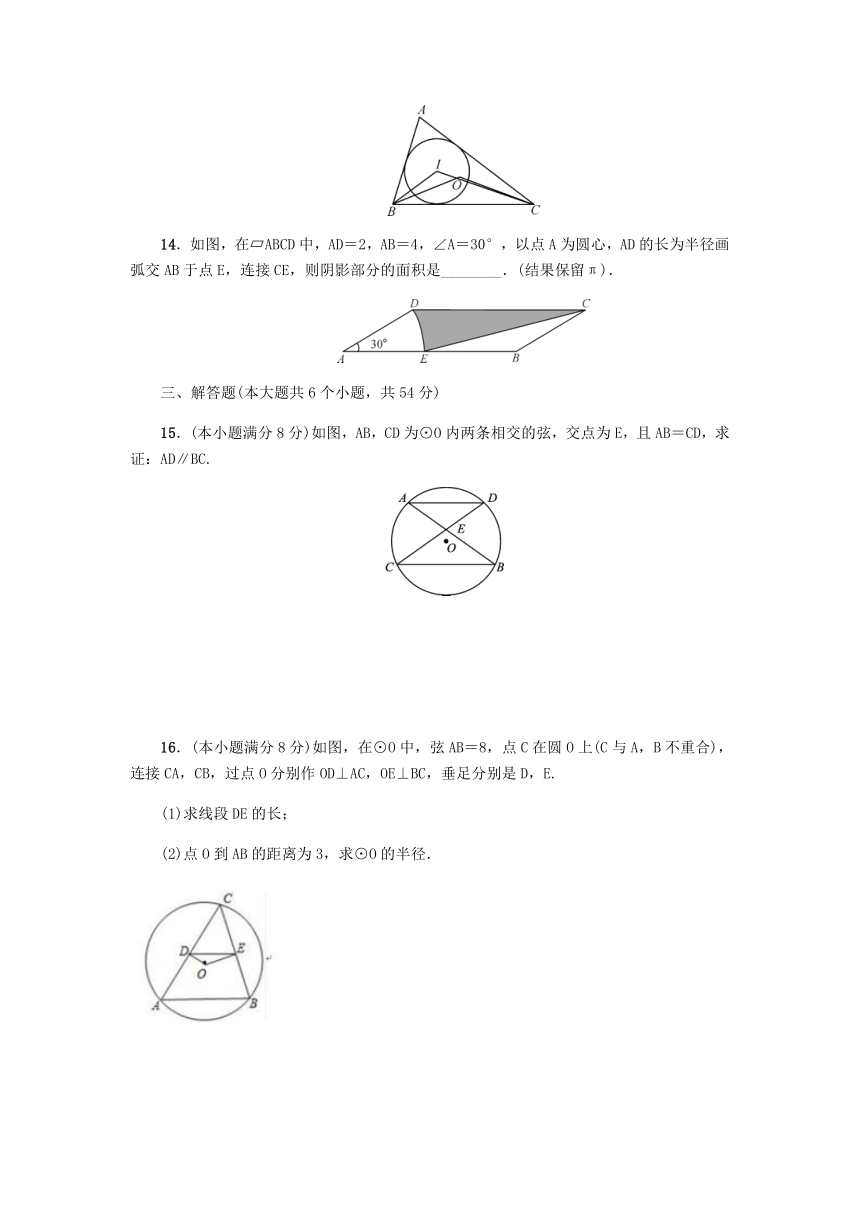
14.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是________.(结果保留π).
三、解答题(本大题共6个小题,共54分)
15.(本小题满分8分)如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
16.(本小题满分8分)如图,在⊙O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA,CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是D,E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求⊙O的半径.
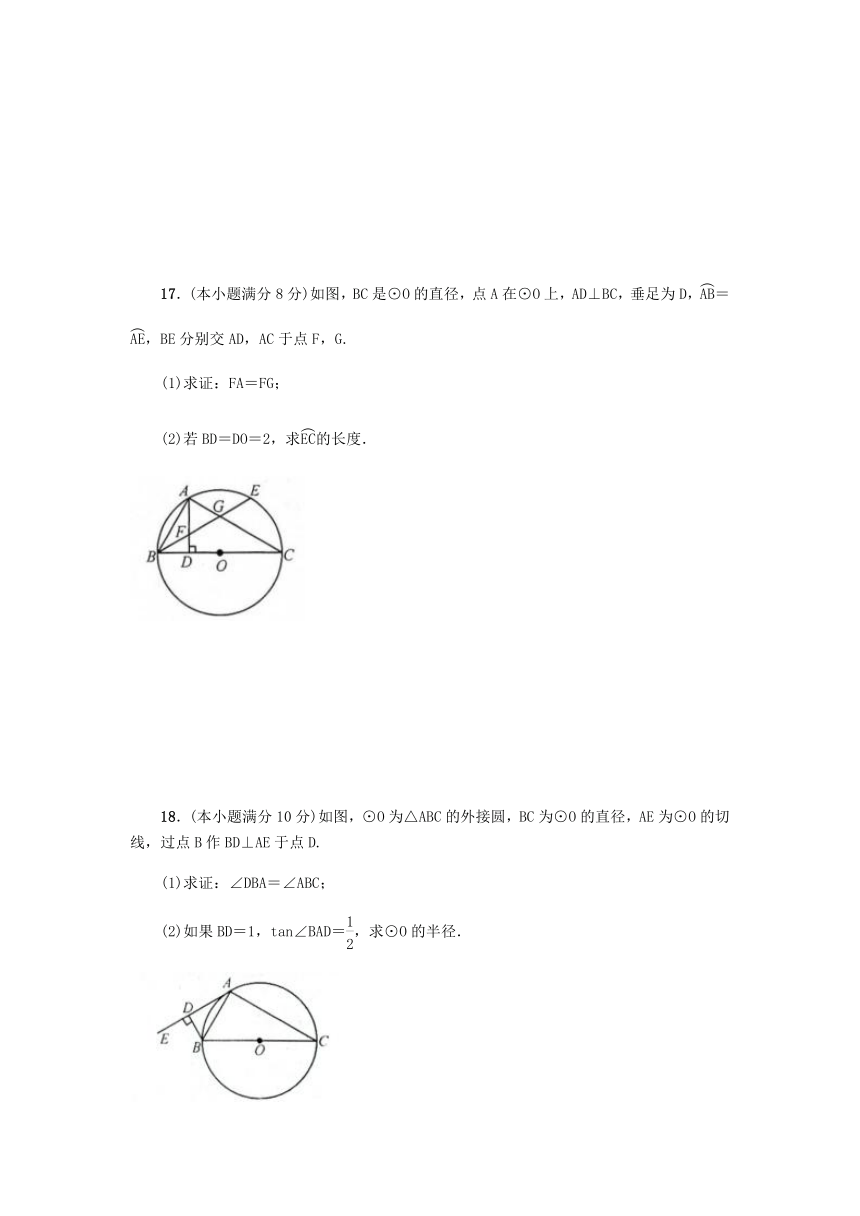
17.(本小题满分8分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
18.(本小题满分10分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=,求⊙O的半径.
19.(本小题满分10分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
20.(本小题满分10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,分别与AC,AB相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.如图,BA,BC是⊙O的两条弦,以点B为圆心,任意长为半径画弧,分别交BA,BC于点M,N.分别以点M,N为圆心,以大于MN为半径画弧,两弧交于点P,连接BP并延长交⊙O于点D,连接OD,OC.若∠COD=70°,则∠ABD等于________.
22.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB=________.
23.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径是7,则GE+FH的最大值是________.
24.如图,在矩形ABCD中,已知AB=6,BC=4,以CD为直径作⊙O,将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为M,边CD′与⊙O相交于点N,则CN的长为________.
25.如图,直线y=-x+m(m>0)分别与x轴、y轴交于点A,B,C是AB的中点,点D在直线y=-2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是________.
二、解答题(本大题共3个小题,共30分)
26.(本小题满分8分)如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6
cm时.
①直接写出扇形AOB的面积约为________.cm2(结果精确到1
cm2);
②点E是⊙O上一动点(点E不与点A,B重合),连接AE,BE,请直接写出∠AEB=________.
27.(本小题满分10分)如图,AB为⊙O的直径,C,D为⊙O上异于A,B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,垂足为E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC.
①求证:CF是⊙O的切线;
②当BD=6,tanF=时,求CF的长.
28.(本小题满分12分)如图1,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是⊙O的切线;
(2)如图2,若A为EH的中点,求的值;
(3)如图2,若EA=EF=1,求⊙O的半径.
图1
图2
参考答案
2020-2021学年北师大版九年级数学下册第三章
圆
单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
B
A
B
C
A
B
C
B
1.下列说法正确的是(B)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(C)
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(B)
A.70°
B.60°
C.50°
D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(A)
A.r=R
B.r=R
C.r=R
D.r=R
5.如图,在平面直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为(B)
A.12
B.10
C.14
D.15
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(C)
A.(2,-1)
B.(2,2)
C.(2,1)
D.(3,1)
7.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D.若⊙O的直径为5,BC=4,则AB的长为(A)
A.2
B.2
C.4
D.5
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于(B)
A.70°
B.64°
C.62°
D.51°
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10
cm处,铁片与直尺的唯一公共点A落在直尺14
cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(C)
A.圆形铁片的半径是4
cm
B.四边形AOBC为正方形
C.的长度为4π
cm
D.扇形OAB的面积是4π
cm2
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a
的值是(B)
A.4
B.3+
C.3
D.3+
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=147°.
12.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有∠6,∠2,∠5.
13.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为125°.
14.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是3-π(结果保留π).
三、解答题(本大题共6个小题,共54分)
15.(本小题满分8分)如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
证明:∵AB=CD,
∴
=.
∴-=-,即
=.
∴∠A=∠B.
∴AD∥BC.
16.(本小题满分8分)如图,在⊙O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA,CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是D,E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求⊙O的半径.
解:(1)∵OD⊥AC,DE⊥BC,∴AD=DC,CE=EB.
∴DE是△ABC的中位线,∴DE=AB.
∵AB=8,∴DE=4.
(2)过点O作OH⊥AB,垂足为H,连接OA,
∴AH=BH=AB=4.
在Rt△AHO中,OH=3,AH2+OH2=AO2,∴AO=5,即⊙O的半径为5.
17.(本小题满分8分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
解:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°.∴∠ABE+∠AGB=90°.
∵AD⊥BC,∴∠C+∠CAD=90°.∵=,∴∠C=∠ABE.
∴∠AGB=∠CAD.∴FA=FG.
(2)连接AO,EO.∵BD=DO=2,AD⊥BC,∴AB=AO.
∵AO=BO,∴AB=AO=BO.
∴△ABO是等边三角形.∴∠AOB=60°.∵=,∴∠AOE=60°.∴∠EOC=60°.
∴的长为π×(2+2)×=π.
18.(本小题满分10分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=,求⊙O的半径.
解:(1)证明:连接OA.
∵AE为⊙O的切线,BD⊥AE,∴∠DAO=∠EDB=90°.
∴DB∥AO.∴∠DBA=∠BAO.
又∵OA=OB,∴∠ABC=∠BAO.∴∠DBA=∠ABC.
(2)∵BD=1,tan∠BAD=,∴AD=2.∴AB==.∴cos∠DBA=.
∵∠DBA=∠CBA,∴BC===5.∴⊙O的半径为2.5.
19.(本小题满分10分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD.∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴EB=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.解得BE=.
20.(本小题满分10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,分别与AC,AB相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
解:(1)证明:连接OD.
∵⊙O与BC相切于点D,∴OD⊥BC.
∵∠C=90°,∴OD∥AC.∴∠CAD=∠ODA.
∵OA=OD,∴∠OAD=∠ODA.∴∠CAD=∠BAD.∴AD平分∠CAB.
(2)①DF=DH.理由如下:
∵FH平分∠AFE,∴∠AFH=∠EFH.
又∵AD平分∠CAB,∴∠DFG=∠EAD=∠HAF.
∴∠DFG+∠GFH=∠HAF+∠HFA,即∠DFH=∠DHF.∴DF=DH.
②设HG=x,则DH=DF=1+x.
∵OH⊥AD,∴AD=2DH=2(1+x).
∵∠DFG=∠DAF,∠FDG=∠FDA,∴△DFG∽△DAF.∴=.∴=.∴x=1.
∵AF为直径,∴∠ADF=90°.∴AF===2.∴⊙O的半径为.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.如图,BA,BC是⊙O的两条弦,以点B为圆心,任意长为半径画弧,分别交BA,BC于点M,N.分别以点M,N为圆心,以大于MN为半径画弧,两弧交于点P,连接BP并延长交⊙O于点D,连接OD,OC.若∠COD=70°,则∠ABD等于35°.
22.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB=119°.
23.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径是7,则GE+FH的最大值是10.5.
24.如图,在矩形ABCD中,已知AB=6,BC=4,以CD为直径作⊙O,将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为M,边CD′与⊙O相交于点N,则CN的长为4.
25.如图,直线y=-x+m(m>0)分别与x轴、y轴交于点A,B,C是AB的中点,点D在直线y=-2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是3.
二、解答题(本大题共3个小题,共30分)
26.(本小题满分8分)如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6
cm时.
①直接写出扇形AOB的面积约为31
cm2(结果精确到1
cm2);
②点E是⊙O上一动点(点E不与点A,B重合),连接AE,BE,请直接写出∠AEB=50或130°.
证明:∵OA=OB,∴∠OBA=∠OAB.
∵直线BC与⊙O相切,∴OB⊥CB.
又∵AD⊥BC,∴OB∥AD.
∴∠OBA=∠DAB.
∴∠OAB=∠DAB.
∴AB平分∠OAD.
27.(本小题满分10分)如图,AB为⊙O的直径,C,D为⊙O上异于A,B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,垂足为E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC.
①求证:CF是⊙O的切线;
②当BD=6,tanF=时,求CF的长.
解:(1)证明:∵AB为⊙O的直径,∴∠ADB=90°.
∴AD⊥DB,∵CE⊥DB,∴AD∥CF.
∴∠DAC+∠ACF=180°.
(2)连接OC,
∵OA=OC,∴∠OAC=∠OCA.
又∵∠COB=∠OAC+∠OCA,∴∠COB=2∠OAC.
又∵∠DBA=2∠BDC,∠BDC=∠OAC,
∴∠DBA=2∠OAC,∴∠DBA=∠COB,∴OC∥DB.
∵CE⊥DB,∴OC⊥CF.
又∵OC为⊙O的半径,∴CF为⊙O的切线.
②∵CF∥AD,∴∠BAD=∠F,∴tan∠BAD=tanF==.
∵BD=6,∴AD=BD=8,∴AB==10,∴OB=OC=5.
∵OC⊥CF,∴∠OCF=90°,∴tanF==,解得CF=.
28.(本小题满分12分)如图1,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是⊙O的切线;
(2)如图2,若A为EH的中点,求的值;
(3)如图2,若EA=EF=1,求⊙O的半径.
证明:(1)连接OD,
∵OB=OD,∴△ODB是等腰三角形.
∠OBD=∠ODB①.
在△ABC中,∵AB=AC,∴∠ABC=∠ACB②.
由①②得∠ODB=∠OBD=∠ACB,∴OD∥AC.
∵DH⊥AC,∴DH⊥OD.
又∵OD为⊙O的半径,∴DH是⊙O的切线.
(2)在⊙O中,∵∠E=∠B,∴由(1)可知∠E=∠B=∠C,
∴△EDC是等腰三角形.
∵DH⊥AC,且点A是EH中点,设AE=x,EC=4x,则AC=3x.
连接OD,AD,则在⊙O中,∠ADB=90°,AD⊥BD,∵AB=AC,∴D是BC的中点.
∴OD是△ABC的中位线,∴OD∥AC,OD=AC=×3x
=.
∵OD∥AC,∴∠E=∠ODF.
在△AEF和△ODF中,∵∠E=∠ODF,∠AFE=∠OFD,∴△AEF∽△ODF.
∴=,∴==,∴=.
(3)设⊙O的半径为r,即OD=OB=r.
∵EF=EA,∴∠EFA=∠EAF.
∵OD∥EC,∴∠FOD=∠EAF.
则∠FOD=∠EAF=∠EFA=∠OFD.
∴DF=OD=r,∴DE=DF+EF=r+1,∴BD=CD=DE=r+1.
在⊙O中,∵∠BDE=∠EAB,∴∠BFD=∠EFA=∠EAB=∠BDE,∴BF=BD,△BDF是等腰三角形.
∴BF=BD=r+1,∴AF=AB-BF=2OB-BF=2r-(1+r)=r-1.
在△BFD和△EFA中,
∵∠BFD=∠EFA
,∠B=∠E,∴△BFD∽△EFA,∴=,∴=.
解得r1=,r2=(舍去).
综上所述,⊙O的半径为.
圆
单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.下列说法正确的是(
)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(
)
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(
)
A.70°
B.60°
C.50°
D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(
)
A.r=R
B.r=R
C.r=R
D.r=R
5.如图,在平面直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为(
)
A.12
B.10
C.14
D.15
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(
)
A.(2,-1)
B.(2,2)
C.(2,1)
D.(3,1)
7.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D.若⊙O的直径为5,BC=4,则AB的长为(
)
A.2
B.2
C.4
D.5
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于(
)
A.70°
B.64°
C.62°
D.51°
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10
cm处,铁片与直尺的唯一公共点A落在直尺14
cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(
)
A.圆形铁片的半径是4
cm
B.四边形AOBC为正方形
C.的长度为4π
cm
D.扇形OAB的面积是4π
cm2
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a
的值是(
)
A.4
B.3+
C.3
D.3+
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=________.
12.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有________.
13.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为________.
14.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是________.(结果保留π).
三、解答题(本大题共6个小题,共54分)
15.(本小题满分8分)如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
16.(本小题满分8分)如图,在⊙O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA,CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是D,E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求⊙O的半径.
17.(本小题满分8分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
18.(本小题满分10分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=,求⊙O的半径.
19.(本小题满分10分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
20.(本小题满分10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,分别与AC,AB相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.如图,BA,BC是⊙O的两条弦,以点B为圆心,任意长为半径画弧,分别交BA,BC于点M,N.分别以点M,N为圆心,以大于MN为半径画弧,两弧交于点P,连接BP并延长交⊙O于点D,连接OD,OC.若∠COD=70°,则∠ABD等于________.
22.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB=________.
23.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径是7,则GE+FH的最大值是________.
24.如图,在矩形ABCD中,已知AB=6,BC=4,以CD为直径作⊙O,将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为M,边CD′与⊙O相交于点N,则CN的长为________.
25.如图,直线y=-x+m(m>0)分别与x轴、y轴交于点A,B,C是AB的中点,点D在直线y=-2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是________.
二、解答题(本大题共3个小题,共30分)
26.(本小题满分8分)如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6
cm时.
①直接写出扇形AOB的面积约为________.cm2(结果精确到1
cm2);
②点E是⊙O上一动点(点E不与点A,B重合),连接AE,BE,请直接写出∠AEB=________.
27.(本小题满分10分)如图,AB为⊙O的直径,C,D为⊙O上异于A,B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,垂足为E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC.
①求证:CF是⊙O的切线;
②当BD=6,tanF=时,求CF的长.
28.(本小题满分12分)如图1,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是⊙O的切线;
(2)如图2,若A为EH的中点,求的值;
(3)如图2,若EA=EF=1,求⊙O的半径.
图1
图2
参考答案
2020-2021学年北师大版九年级数学下册第三章
圆
单元测试题
(时间:120分钟 满分:150分)
A卷(共100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
B
A
B
C
A
B
C
B
1.下列说法正确的是(B)
A.直径是弦,弦是直径
B.半圆是轴对称图形
C.无论过圆内哪一点,只能作一条直径
D.直径的长度是半径的2倍
2.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是(C)
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是(B)
A.70°
B.60°
C.50°
D.30°
4.一个正六边形的半径为R,边心距为r,那么R与r的关系是(A)
A.r=R
B.r=R
C.r=R
D.r=R
5.如图,在平面直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为(B)
A.12
B.10
C.14
D.15
6.如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1)四点,则该圆圆心的坐标为(C)
A.(2,-1)
B.(2,2)
C.(2,1)
D.(3,1)
7.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D.若⊙O的直径为5,BC=4,则AB的长为(A)
A.2
B.2
C.4
D.5
8.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到点D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于(B)
A.70°
B.64°
C.62°
D.51°
9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺10
cm处,铁片与直尺的唯一公共点A落在直尺14
cm处,铁片与三角尺的唯一公共点为点B.下列说法错误的是(C)
A.圆形铁片的半径是4
cm
B.四边形AOBC为正方形
C.的长度为4π
cm
D.扇形OAB的面积是4π
cm2
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a
的值是(B)
A.4
B.3+
C.3
D.3+
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=147°.
12.如图,在⊙O的内接四边形ABCD中,AB=CD,则图中与∠1相等的角有∠6,∠2,∠5.
13.如图,点O为△ABC的外心,点I为△ABC的内心.若∠BOC=140°,则∠BIC的度数为125°.
14.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是3-π(结果保留π).
三、解答题(本大题共6个小题,共54分)
15.(本小题满分8分)如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
证明:∵AB=CD,
∴
=.
∴-=-,即
=.
∴∠A=∠B.
∴AD∥BC.
16.(本小题满分8分)如图,在⊙O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA,CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是D,E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求⊙O的半径.
解:(1)∵OD⊥AC,DE⊥BC,∴AD=DC,CE=EB.
∴DE是△ABC的中位线,∴DE=AB.
∵AB=8,∴DE=4.
(2)过点O作OH⊥AB,垂足为H,连接OA,
∴AH=BH=AB=4.
在Rt△AHO中,OH=3,AH2+OH2=AO2,∴AO=5,即⊙O的半径为5.
17.(本小题满分8分)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求的长度.
解:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°.∴∠ABE+∠AGB=90°.
∵AD⊥BC,∴∠C+∠CAD=90°.∵=,∴∠C=∠ABE.
∴∠AGB=∠CAD.∴FA=FG.
(2)连接AO,EO.∵BD=DO=2,AD⊥BC,∴AB=AO.
∵AO=BO,∴AB=AO=BO.
∴△ABO是等边三角形.∴∠AOB=60°.∵=,∴∠AOE=60°.∴∠EOC=60°.
∴的长为π×(2+2)×=π.
18.(本小题满分10分)如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于点D.
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=,求⊙O的半径.
解:(1)证明:连接OA.
∵AE为⊙O的切线,BD⊥AE,∴∠DAO=∠EDB=90°.
∴DB∥AO.∴∠DBA=∠BAO.
又∵OA=OB,∴∠ABC=∠BAO.∴∠DBA=∠ABC.
(2)∵BD=1,tan∠BAD=,∴AD=2.∴AB==.∴cos∠DBA=.
∵∠DBA=∠CBA,∴BC===5.∴⊙O的半径为2.5.
19.(本小题满分10分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD.∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴EB=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.解得BE=.
20.(本小题满分10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,分别与AC,AB相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
解:(1)证明:连接OD.
∵⊙O与BC相切于点D,∴OD⊥BC.
∵∠C=90°,∴OD∥AC.∴∠CAD=∠ODA.
∵OA=OD,∴∠OAD=∠ODA.∴∠CAD=∠BAD.∴AD平分∠CAB.
(2)①DF=DH.理由如下:
∵FH平分∠AFE,∴∠AFH=∠EFH.
又∵AD平分∠CAB,∴∠DFG=∠EAD=∠HAF.
∴∠DFG+∠GFH=∠HAF+∠HFA,即∠DFH=∠DHF.∴DF=DH.
②设HG=x,则DH=DF=1+x.
∵OH⊥AD,∴AD=2DH=2(1+x).
∵∠DFG=∠DAF,∠FDG=∠FDA,∴△DFG∽△DAF.∴=.∴=.∴x=1.
∵AF为直径,∴∠ADF=90°.∴AF===2.∴⊙O的半径为.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在题中的横线上)
21.如图,BA,BC是⊙O的两条弦,以点B为圆心,任意长为半径画弧,分别交BA,BC于点M,N.分别以点M,N为圆心,以大于MN为半径画弧,两弧交于点P,连接BP并延长交⊙O于点D,连接OD,OC.若∠COD=70°,则∠ABD等于35°.
22.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB=119°.
23.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径是7,则GE+FH的最大值是10.5.
24.如图,在矩形ABCD中,已知AB=6,BC=4,以CD为直径作⊙O,将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为M,边CD′与⊙O相交于点N,则CN的长为4.
25.如图,直线y=-x+m(m>0)分别与x轴、y轴交于点A,B,C是AB的中点,点D在直线y=-2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是3.
二、解答题(本大题共3个小题,共30分)
26.(本小题满分8分)如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6
cm时.
①直接写出扇形AOB的面积约为31
cm2(结果精确到1
cm2);
②点E是⊙O上一动点(点E不与点A,B重合),连接AE,BE,请直接写出∠AEB=50或130°.
证明:∵OA=OB,∴∠OBA=∠OAB.
∵直线BC与⊙O相切,∴OB⊥CB.
又∵AD⊥BC,∴OB∥AD.
∴∠OBA=∠DAB.
∴∠OAB=∠DAB.
∴AB平分∠OAD.
27.(本小题满分10分)如图,AB为⊙O的直径,C,D为⊙O上异于A,B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,垂足为E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC.
①求证:CF是⊙O的切线;
②当BD=6,tanF=时,求CF的长.
解:(1)证明:∵AB为⊙O的直径,∴∠ADB=90°.
∴AD⊥DB,∵CE⊥DB,∴AD∥CF.
∴∠DAC+∠ACF=180°.
(2)连接OC,
∵OA=OC,∴∠OAC=∠OCA.
又∵∠COB=∠OAC+∠OCA,∴∠COB=2∠OAC.
又∵∠DBA=2∠BDC,∠BDC=∠OAC,
∴∠DBA=2∠OAC,∴∠DBA=∠COB,∴OC∥DB.
∵CE⊥DB,∴OC⊥CF.
又∵OC为⊙O的半径,∴CF为⊙O的切线.
②∵CF∥AD,∴∠BAD=∠F,∴tan∠BAD=tanF==.
∵BD=6,∴AD=BD=8,∴AB==10,∴OB=OC=5.
∵OC⊥CF,∴∠OCF=90°,∴tanF==,解得CF=.
28.(本小题满分12分)如图1,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是⊙O的切线;
(2)如图2,若A为EH的中点,求的值;
(3)如图2,若EA=EF=1,求⊙O的半径.
证明:(1)连接OD,
∵OB=OD,∴△ODB是等腰三角形.
∠OBD=∠ODB①.
在△ABC中,∵AB=AC,∴∠ABC=∠ACB②.
由①②得∠ODB=∠OBD=∠ACB,∴OD∥AC.
∵DH⊥AC,∴DH⊥OD.
又∵OD为⊙O的半径,∴DH是⊙O的切线.
(2)在⊙O中,∵∠E=∠B,∴由(1)可知∠E=∠B=∠C,
∴△EDC是等腰三角形.
∵DH⊥AC,且点A是EH中点,设AE=x,EC=4x,则AC=3x.
连接OD,AD,则在⊙O中,∠ADB=90°,AD⊥BD,∵AB=AC,∴D是BC的中点.
∴OD是△ABC的中位线,∴OD∥AC,OD=AC=×3x
=.
∵OD∥AC,∴∠E=∠ODF.
在△AEF和△ODF中,∵∠E=∠ODF,∠AFE=∠OFD,∴△AEF∽△ODF.
∴=,∴==,∴=.
(3)设⊙O的半径为r,即OD=OB=r.
∵EF=EA,∴∠EFA=∠EAF.
∵OD∥EC,∴∠FOD=∠EAF.
则∠FOD=∠EAF=∠EFA=∠OFD.
∴DF=OD=r,∴DE=DF+EF=r+1,∴BD=CD=DE=r+1.
在⊙O中,∵∠BDE=∠EAB,∴∠BFD=∠EFA=∠EAB=∠BDE,∴BF=BD,△BDF是等腰三角形.
∴BF=BD=r+1,∴AF=AB-BF=2OB-BF=2r-(1+r)=r-1.
在△BFD和△EFA中,
∵∠BFD=∠EFA
,∠B=∠E,∴△BFD∽△EFA,∴=,∴=.
解得r1=,r2=(舍去).
综上所述,⊙O的半径为.
