西师大版数学六下2.2圆锥 一课一练(含解析)
文档属性
| 名称 | 西师大版数学六下2.2圆锥 一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.2圆锥 同步练习
一、选择题
1.圆锥的高与底面直径都是4厘米,则圆锥的体积是(?? )立方厘米。
A.?π???????????????????????????????????B.?π???????????????????????????????????C.?16π???????????????????????????????????D.?64π
2.下面的圆柱与圆锥体积相等的是(????? )。(单位:厘米)
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C???????????????????????????????????????????D.?D
3.一个圆柱_???????????????1_8升水,把一个与它等底等高的铁圆锥倒插入杯底,拿出圆锥后,圆柱形杯中还有(????? )水。 【来源:21·世纪·教育·网】
A.?12升?????????????????????????????????????B.?9升?????????????????????????????????????C.?15升?????????????????????????????????????D.?9升
4.一个圆锥的底面半径扩大到原来的3倍,高不变,则它的体积扩大(??? )。
A.?6倍?????????????????????????????????????B.?9倍?????????????????????????????????????C.?18倍?????????????????????????????????????D.?27倍
5.下面图形以虚线为轴快速旋转后形成的图形是(?? )
A.?三角形????????????????????????????????????????B.?圆锥????????????????????????????????????????C.?圆柱21·世纪*教育网
6.—个底面直径是_28cm???é??_是6cm的圆锥形木块,锯成形状、大小完全相同的两个木块后,表面积比原来增加(?? )。 21*cnjy*com
A.?84cm???????????????????????????????B.?168cm???????????????????????????????C.?186cm???????????????????????????????D.?336cm?
二、判断题
7.正方体、长方体、圆柱和圆锥的体积都可以用“底面积×高”来计算。( ??)
8.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。( ???)
9.圆锥的底面是一个椭圆。(?? )
10.圆锥的侧面展开后是一个等腰三角形。(?? )
三、填空题
11.一堆玉米成圆锥形,底面周长是18.84米,高1米,把它装入底面是2平方米的圆柱形粮囤中,能装________米高。 21世纪教育网版权所有
12.有一根半径是2厘米,高6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去________立方厘米钢材。 21教育网
13.一堆6.28立方米的煤,近似于一个圆锥。测量出底面直径是4米,这堆煤大约高________厘米。
14.一个圆锥的底面半径是3厘米,体积为18.84立方厘米,这个圆锥的高是________厘米.
四、计算题
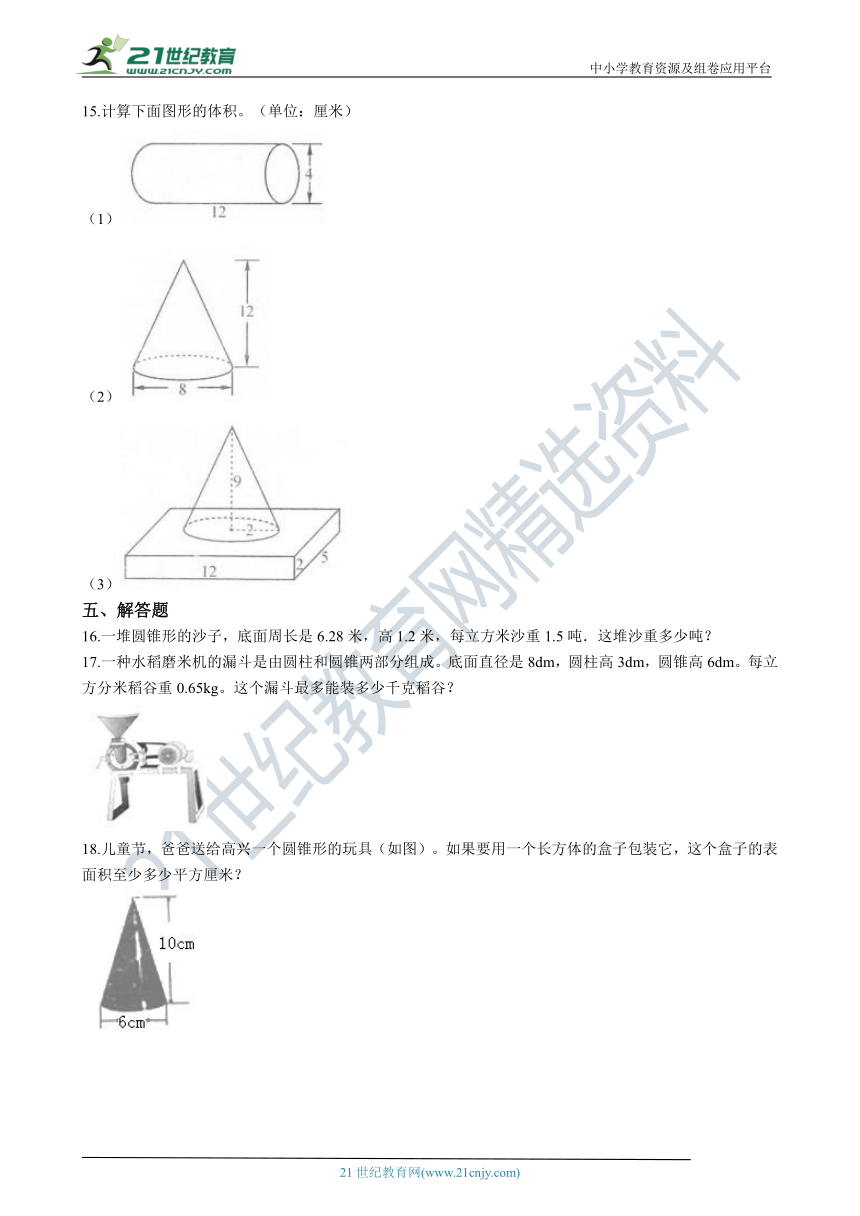
15.计算下面图形的体积。(单位:厘米)
(1)
(2)
(3)
五、解答题
16.一堆圆锥形的沙子,底面周长是6.28米,高1.2米,每立方米沙重1.5吨.这堆沙重多少吨?
17.一种水稻磨_?±????????????????_由圆柱和圆锥两部分组成。底面直径是8dm,圆柱高3dm,圆锥高6dm。每立方分米稻谷重0.65kg。这个漏斗最多能装多少千克稻谷? 21cnjy.com
18.儿童节,爸爸送给高兴一个圆锥形的玩具(如图)。如果要用一个长方体的盒子包装它,这个盒子的表面积至少多少平方厘米? 21·cn·jy·com
答案解析部分
一、选择题
1. A
【解答】(4÷2)2×π×4×=π,所以圆锥的体积是π。
故答案为:A。
分析:圆锥的体积=π×(直径÷2)2×h,据此作答即可。www.21-cn-jy.com
2. C
【解答】圆锥的体积是:3.14×(12÷2)2×15×=565.2立方厘米。
图形A与圆锥等底等高,所以,它与圆锥的体积不相等;
图形B的体积是:3.14×(4÷2)2×15=188.4立方厘米;
图形C的底面与圆锥的底面相等,高是圆锥的, 所以,图形C的体积与圆锥的体积相等;
图形D的底面与圆锥的底面不相等,高是圆锥的, 所以,图形C的体积与圆锥的体积不相等;
故答案为:C。
分析:圆锥的体积=×πr2h;圆柱的体积=πr2h。据此作答即可。www-2-1-cnjy-com
3. A
【解答】18×=12(升)
故答案为:A。
分析: 一个与圆柱等底等高的铁圆锥的体积是圆柱体积的, 拿出圆锥后,圆柱形杯中还有的水。
4. B
【解答】一个圆锥的底面半径扩大到原来的3倍,高不变,则它的体积扩大3×3=9倍。
故答案为:B。 2-1-c-n-j-y
分析:圆锥的体积=πr2h,当底面半径扩大到原来的3倍,高不变时,现在它的体积=π(r×3)2h= πr2h×9。
5. B
【解答】下面_????????????è?????_为轴快速旋转后形成的图形是圆锥。
故答案为:B。
分析:以直角三角形的一条直角边为轴旋转一周形成的图形是圆锥,为轴的直角边是圆锥的高,另一条直角边就是圆锥的底面半径。【来源:21cnj*y.co*m】
6. B
【解答】28×6÷2×2=168cm2 , 所以表面积比原来增加168cm2。
故答案为:B。 【出处:21教育名师】
分析:把一_??????é??é????????_状、大小完全相同的两个木块,就是沿着圆锥的顶点垂直于底面切开,所以会增加两个三角形面,其中三角形的底=圆锥的底面周长,三角形的高=圆锥的高,所以增加的表面积=三角形的底×三角形的高÷2×2。21教育名师原创作品
二、判断题
7. 错误
【解答】正方体、长方体、圆柱体积都可以用“底面积×高”来计算,圆锥的体积用“底面积×高×”来计算。原题说法错误。
故答案为:错误。
分析:等底等高的圆柱体积是圆锥体积的3倍,所以圆锥的体积=底面积×高×。
8. 错误
【解答】 以三角形的一条边为轴旋转一周得到的不一定是一个圆锥体。
故答案为:错误。
分析:以直角三角形的一条直角边为轴,旋转一周得到的才是一个圆锥体,如果以斜边为轴旋转一周,得到的就不是一个圆锥体。21*cnjy*com
9. 错误
【解答】_???é????????_面是一个圆,即说法错误。
故答案为:错误。
分析:圆锥是一种几何图形,立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。 垂直于轴的边旋转而成的曲面叫做圆锥的底面,圆锥的底面是一个圆形。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
10. 错误
【解答】圆锥的侧面展开后是一个扇形,原说法错误。
故答案为:错误。
分析:
圆锥的侧面展开后是一个扇形,据图判断即可。
三、填空题
11. 4.71
【解答】r=18.84÷3.14÷2=3(米),圆锥的体积=×3.14×3×3×1=9.42(立方米),
能装:9.42÷2=4.71(米)
故答案为:4.71。
分析:先根据周长求出圆锥的底面半径,半径=面积÷3.14÷2,再求出圆锥形玉米的体积,圆锥的体积=×底面积×高,装入圆柱形粮囤中,体积不变,由圆柱的高=体积÷底面积即可求出。
12. 50.24
【解答】3.14×22×6-3.14×22×6×
=3.14×24-3.14×8
=3.14×16
=50.24(立方厘米)
故答案为:50.24。 【版权所有:21教育】
分析:圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 用圆柱的体积减去圆锥的体积即可求出要切去钢材的体积。
13. 150
【解答】6_.28??3?·_[(4÷2)2×3.14]=1.5米=150厘米,所以这堆煤大约高150厘米。
故答案为:150。
分析:这堆煤的高=这堆煤的体积×3÷底面积,其中底面积=(底面直径÷2)2×π,然后进行单位换算,即1米=100厘米。
14. 2
【解答】18.84×3÷(3.14×32)
=56.52÷28.26
=2(厘米)
故答案为:2。
分析:圆锥的体积=底面积×高×, 高=圆锥的体积×3÷底面积,根据公式计算即可。
四、计算题
15. (1)12×(4÷2)2×3.14
=12×4×3.14
=48×3.14
=150.72(立方厘来)
(2)×12×(8÷2)2×3.14
=4×50.24
=200.96(立方厘米)
(3)12×2×5+×22×3.14×9
=120+4×3.14×3
=157.68(立方厘米) 2·1·c·n·j·y
分析:圆柱的体积=(底面直径÷2)2×π×h;圆锥的体积=×(底面直径÷2)2×π×h;长方体的体积=长×宽。据此作答即可。
五、解答题
16. 6.28÷3.14÷2=1(米)
3.14×12×1.2× ×1.5
=3.14×0.4×1.5
=3.14×0.6
=1.884(吨)
答:这堆沙重1.884吨。
分析:这堆沙的底面半径=这堆沙的底面周长÷π÷2,那么这堆沙的体积=πr2h,故这堆沙的重量=这堆沙的体积×每立方米沙的重量。
17. 体积:3.14×(8÷2)2×3+3.14×(8÷2)2×6×
=50.24×(3+2)
=251.2(立方分米)
装稻谷:251.2×0.65=163.28(千克)
答: 这个漏斗最多能装163.28千克稻谷。?
分析:圆柱的体积=π×(底面直径÷2)2×圆柱的高,圆锥的体积=π×(底面直径÷2)2×圆锥的高×, 装稻谷的数量=(圆柱的体积+圆锥的体积)×每立方分米稻谷重量。
18. 6×6×2+6×10×4
=72+240
=312(平方厘米)
答:这个盒子的表面积至少312平方厘米。
分析:盒子的底面边长至少是6cm,高至少是10cm,根据长方体表面积公式计算盒子的表面积即可。
_21?????????è?????(www.21cnjy.com)_
2.2圆锥 同步练习
一、选择题
1.圆锥的高与底面直径都是4厘米,则圆锥的体积是(?? )立方厘米。
A.?π???????????????????????????????????B.?π???????????????????????????????????C.?16π???????????????????????????????????D.?64π
2.下面的圆柱与圆锥体积相等的是(????? )。(单位:厘米)
A.?A???????????????????????????????????????????B.?B???????????????????????????????????????????C.?C???????????????????????????????????????????D.?D
3.一个圆柱_???????????????1_8升水,把一个与它等底等高的铁圆锥倒插入杯底,拿出圆锥后,圆柱形杯中还有(????? )水。 【来源:21·世纪·教育·网】
A.?12升?????????????????????????????????????B.?9升?????????????????????????????????????C.?15升?????????????????????????????????????D.?9升
4.一个圆锥的底面半径扩大到原来的3倍,高不变,则它的体积扩大(??? )。
A.?6倍?????????????????????????????????????B.?9倍?????????????????????????????????????C.?18倍?????????????????????????????????????D.?27倍
5.下面图形以虚线为轴快速旋转后形成的图形是(?? )
A.?三角形????????????????????????????????????????B.?圆锥????????????????????????????????????????C.?圆柱21·世纪*教育网
6.—个底面直径是_28cm???é??_是6cm的圆锥形木块,锯成形状、大小完全相同的两个木块后,表面积比原来增加(?? )。 21*cnjy*com
A.?84cm???????????????????????????????B.?168cm???????????????????????????????C.?186cm???????????????????????????????D.?336cm?
二、判断题
7.正方体、长方体、圆柱和圆锥的体积都可以用“底面积×高”来计算。( ??)
8.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。( ???)
9.圆锥的底面是一个椭圆。(?? )
10.圆锥的侧面展开后是一个等腰三角形。(?? )
三、填空题
11.一堆玉米成圆锥形,底面周长是18.84米,高1米,把它装入底面是2平方米的圆柱形粮囤中,能装________米高。 21世纪教育网版权所有
12.有一根半径是2厘米,高6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去________立方厘米钢材。 21教育网
13.一堆6.28立方米的煤,近似于一个圆锥。测量出底面直径是4米,这堆煤大约高________厘米。
14.一个圆锥的底面半径是3厘米,体积为18.84立方厘米,这个圆锥的高是________厘米.
四、计算题
15.计算下面图形的体积。(单位:厘米)
(1)
(2)
(3)
五、解答题
16.一堆圆锥形的沙子,底面周长是6.28米,高1.2米,每立方米沙重1.5吨.这堆沙重多少吨?
17.一种水稻磨_?±????????????????_由圆柱和圆锥两部分组成。底面直径是8dm,圆柱高3dm,圆锥高6dm。每立方分米稻谷重0.65kg。这个漏斗最多能装多少千克稻谷? 21cnjy.com
18.儿童节,爸爸送给高兴一个圆锥形的玩具(如图)。如果要用一个长方体的盒子包装它,这个盒子的表面积至少多少平方厘米? 21·cn·jy·com
答案解析部分
一、选择题
1. A
【解答】(4÷2)2×π×4×=π,所以圆锥的体积是π。
故答案为:A。
分析:圆锥的体积=π×(直径÷2)2×h,据此作答即可。www.21-cn-jy.com
2. C
【解答】圆锥的体积是:3.14×(12÷2)2×15×=565.2立方厘米。
图形A与圆锥等底等高,所以,它与圆锥的体积不相等;
图形B的体积是:3.14×(4÷2)2×15=188.4立方厘米;
图形C的底面与圆锥的底面相等,高是圆锥的, 所以,图形C的体积与圆锥的体积相等;
图形D的底面与圆锥的底面不相等,高是圆锥的, 所以,图形C的体积与圆锥的体积不相等;
故答案为:C。
分析:圆锥的体积=×πr2h;圆柱的体积=πr2h。据此作答即可。www-2-1-cnjy-com
3. A
【解答】18×=12(升)
故答案为:A。
分析: 一个与圆柱等底等高的铁圆锥的体积是圆柱体积的, 拿出圆锥后,圆柱形杯中还有的水。
4. B
【解答】一个圆锥的底面半径扩大到原来的3倍,高不变,则它的体积扩大3×3=9倍。
故答案为:B。 2-1-c-n-j-y
分析:圆锥的体积=πr2h,当底面半径扩大到原来的3倍,高不变时,现在它的体积=π(r×3)2h= πr2h×9。
5. B
【解答】下面_????????????è?????_为轴快速旋转后形成的图形是圆锥。
故答案为:B。
分析:以直角三角形的一条直角边为轴旋转一周形成的图形是圆锥,为轴的直角边是圆锥的高,另一条直角边就是圆锥的底面半径。【来源:21cnj*y.co*m】
6. B
【解答】28×6÷2×2=168cm2 , 所以表面积比原来增加168cm2。
故答案为:B。 【出处:21教育名师】
分析:把一_??????é??é????????_状、大小完全相同的两个木块,就是沿着圆锥的顶点垂直于底面切开,所以会增加两个三角形面,其中三角形的底=圆锥的底面周长,三角形的高=圆锥的高,所以增加的表面积=三角形的底×三角形的高÷2×2。21教育名师原创作品
二、判断题
7. 错误
【解答】正方体、长方体、圆柱体积都可以用“底面积×高”来计算,圆锥的体积用“底面积×高×”来计算。原题说法错误。
故答案为:错误。
分析:等底等高的圆柱体积是圆锥体积的3倍,所以圆锥的体积=底面积×高×。
8. 错误
【解答】 以三角形的一条边为轴旋转一周得到的不一定是一个圆锥体。
故答案为:错误。
分析:以直角三角形的一条直角边为轴,旋转一周得到的才是一个圆锥体,如果以斜边为轴旋转一周,得到的就不是一个圆锥体。21*cnjy*com
9. 错误
【解答】_???é????????_面是一个圆,即说法错误。
故答案为:错误。
分析:圆锥是一种几何图形,立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。 垂直于轴的边旋转而成的曲面叫做圆锥的底面,圆锥的底面是一个圆形。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。
10. 错误
【解答】圆锥的侧面展开后是一个扇形,原说法错误。
故答案为:错误。
分析:
圆锥的侧面展开后是一个扇形,据图判断即可。
三、填空题
11. 4.71
【解答】r=18.84÷3.14÷2=3(米),圆锥的体积=×3.14×3×3×1=9.42(立方米),
能装:9.42÷2=4.71(米)
故答案为:4.71。
分析:先根据周长求出圆锥的底面半径,半径=面积÷3.14÷2,再求出圆锥形玉米的体积,圆锥的体积=×底面积×高,装入圆柱形粮囤中,体积不变,由圆柱的高=体积÷底面积即可求出。
12. 50.24
【解答】3.14×22×6-3.14×22×6×
=3.14×24-3.14×8
=3.14×16
=50.24(立方厘米)
故答案为:50.24。 【版权所有:21教育】
分析:圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 用圆柱的体积减去圆锥的体积即可求出要切去钢材的体积。
13. 150
【解答】6_.28??3?·_[(4÷2)2×3.14]=1.5米=150厘米,所以这堆煤大约高150厘米。
故答案为:150。
分析:这堆煤的高=这堆煤的体积×3÷底面积,其中底面积=(底面直径÷2)2×π,然后进行单位换算,即1米=100厘米。
14. 2
【解答】18.84×3÷(3.14×32)
=56.52÷28.26
=2(厘米)
故答案为:2。
分析:圆锥的体积=底面积×高×, 高=圆锥的体积×3÷底面积,根据公式计算即可。
四、计算题
15. (1)12×(4÷2)2×3.14
=12×4×3.14
=48×3.14
=150.72(立方厘来)
(2)×12×(8÷2)2×3.14
=4×50.24
=200.96(立方厘米)
(3)12×2×5+×22×3.14×9
=120+4×3.14×3
=157.68(立方厘米) 2·1·c·n·j·y
分析:圆柱的体积=(底面直径÷2)2×π×h;圆锥的体积=×(底面直径÷2)2×π×h;长方体的体积=长×宽。据此作答即可。
五、解答题
16. 6.28÷3.14÷2=1(米)
3.14×12×1.2× ×1.5
=3.14×0.4×1.5
=3.14×0.6
=1.884(吨)
答:这堆沙重1.884吨。
分析:这堆沙的底面半径=这堆沙的底面周长÷π÷2,那么这堆沙的体积=πr2h,故这堆沙的重量=这堆沙的体积×每立方米沙的重量。
17. 体积:3.14×(8÷2)2×3+3.14×(8÷2)2×6×
=50.24×(3+2)
=251.2(立方分米)
装稻谷:251.2×0.65=163.28(千克)
答: 这个漏斗最多能装163.28千克稻谷。?
分析:圆柱的体积=π×(底面直径÷2)2×圆柱的高,圆锥的体积=π×(底面直径÷2)2×圆锥的高×, 装稻谷的数量=(圆柱的体积+圆锥的体积)×每立方分米稻谷重量。
18. 6×6×2+6×10×4
=72+240
=312(平方厘米)
答:这个盒子的表面积至少312平方厘米。
分析:盒子的底面边长至少是6cm,高至少是10cm,根据长方体表面积公式计算盒子的表面积即可。
_21?????????è?????(www.21cnjy.com)_
