广东省汕头市2012届高三毕业班教学质量检测(数学理)
文档属性
| 名称 | 广东省汕头市2012届高三毕业班教学质量检测(数学理) |

|
|
| 格式 | zip | ||
| 文件大小 | 192.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-11 00:00:00 | ||
图片预览




文档简介
汕 头 市
2011—2012学年度普通高中毕业班教学质量
数学试题(理科)
本试卷共21小题,满分150分.考试时间120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号.试室号.座位号填写在答题卡上.用2B铅笔将试卷类型(A)填涂在答题卡相应位置上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.作答选做题时.请先用2B铅笔填涂选做题的题号对应的信息点,再作答。漏涂.错涂.多涂的.答案无效.
5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
参考公式: 柱体的体积公式V=sh,其中S是柱体的底面积,h为柱体的高.
棱锥的体积公式,其中S是棱锥体的底面积,h为棱锥体的高.
第 一 卷
一、选择题(每小题5分,共40分,每小题给出的四个选项中,只有一项符合题目要求)
1.复数在复平面上对应的点的坐标是 ( )
A. B. C. D.
2.已知等比数列{an}的公比q为正数,且2a3+a4=a5,则q的值为 ( )
A. B.2 C. D.3
3.下列判断错误的是 ( )
A.“”是“”的充分不必要条件
B.命题“”的否定是“”
C.设随机变量
D.若为假命题,则p,q均为假命题
4.右图是某篮球运动员在一个赛季的30场比赛
中得分的茎叶图,则得分的中位数与众数分别
为( )
A.3与3
B.23与3
C.3与23
D.23与23
A. B. C. D.
6.若一个三位数的十位数字比个位数字和百位数字都大,称这个数为 “伞数”。现从1,2,3,4,5,6这六个数字中取3个数,组成无重复数字的三位数,其中“伞数”有 ( )
A.120个 B.80个 C.40个 D.20个
7.如图,半圆的直径AB=6,O为圆心,C为半圆上不同于
A.B的任意一点,若P为半径OC上的动点,
则的最小值是( )
A. B. C. D.
8.用表示非空集合A中的元素个数,定义,若,,且,由的所有可能值构成的集合是S,那么等于( )
A.4 B. 3 C.2 D. 1
第 二 卷
二、填空题:(本大题共6小题,考生作答6小题,每小题5分,满分30分.)
(一)必做题(9~13题)
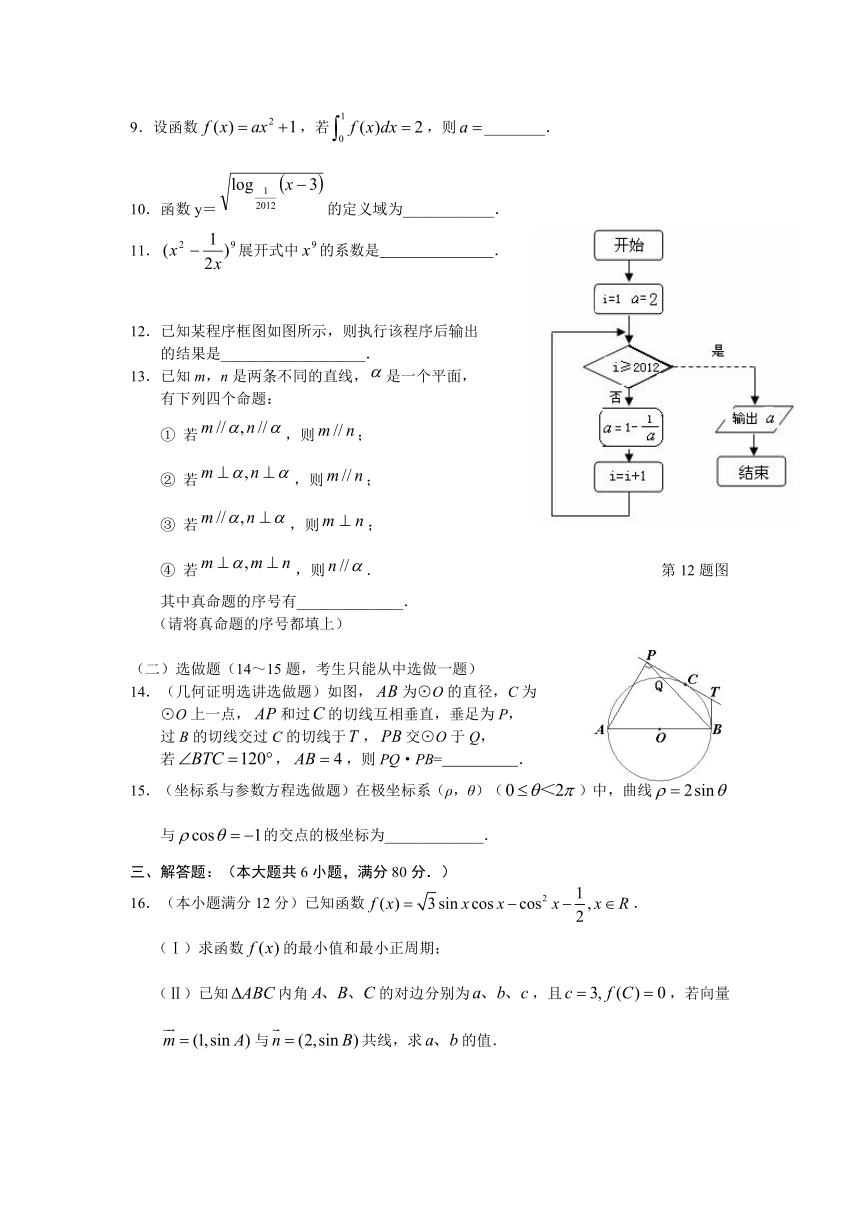
9.设函数,若,则________.
10.函数y=的定义域为____________.
11.展开式中的系数是 .
12.已知某程序框图如图所示,则执行该程序后输出
的结果是___________________.
13.已知m,n是两条不同的直线,是一个平面,
有下列四个命题:
① 若,则;
② 若,则;
③ 若,则;
④ 若,则. 第12题图
其中真命题的序号有______________.
(请将真命题的序号都填上)
(二)选做题(14~15题,考生只能从中选做一题)
14.(几何证明选讲选做题)如图,为⊙O的直径,C为
⊙O上一点,和过的切线互相垂直,垂足为P,
过B的切线交过C的切线于,交⊙O于Q,
若,,则PQ·PB= .
15.(坐标系与参数方程选做题)在极坐标系(ρ,θ)()中,曲线与的交点的极坐标为_____________.
三、解答题:(本大题共6小题,满分80分.)
16.(本小题满分12分)已知函数.
(Ⅰ)求函数的最小值和最小正周期;
(Ⅱ)已知内角的对边分别为,且,若向量与共线,求的值.
17.(本小题满分12分)已知函数f(x)=;
(Ⅰ)证明:函数f(x)在上为减函数;
(Ⅱ)是否存在负数,使得成立,若存在求出;若不存在,请说明理由。
18.(本小题满分14分)如图,为圆柱的母线,是底面圆的直径,
分别是的中点,DE⊥面CBB1.
(Ⅰ)证明:DE //面ABC;
(Ⅱ)求四棱锥与圆柱的体积比;
(Ⅲ)若,求与面所成角的正弦值.
19.(本小题满分14分)
已知汕头市某学校高中部某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查。
(Ⅰ)若要从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;
(Ⅱ)若男学生考前心理状态好的概率为0.6,女学生考前心理状态好的概率为0.5, 表示抽取的5名学生中考前心理状态好的人数,求P(=1)及E.
20.(本小题满分14分)
已知数列满足:
(Ⅰ)探究数列是等差数列还是等比数列,并由此求数列的通项公式;
(Ⅱ)求数列的前n项和
21.(本小题满分14分) 设函数
(Ⅰ)求的单调区间;
(Ⅱ)当时,若方程在上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,.
参考答案
一、选择题 1.A 2.B 3.D 4.D 5.C 6.C 7.A 8.B
7.A 解析:设 , 则
, 所以
8. B 解析:依题意知或,当时,方程恰有1个根,有,得;当时,方程恰有3个根,有,得;故的可能值有3个,故.
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
9. 3 10. (3,4 】 11. 12. 13. ②③
14. 3 15.
三、解答题
①……………………9分
又c=3,由余弦定理,得 ②……………………10分
解方程组①②,得 ……………………12分
17. 解:(1)任取,且
∵ …………4分
∴函数在上为减函数 ………………………6分
另解:如果应用导数证明请相应给分
(2)不存在 ……………………………………………………7分
假设存在负数,使得成立,则 即
………………………10分
与矛盾,
所以不存在负数,使得成立。 ……………………………12分
另解:,由得: 或但,
所以不存在。
18. 解:证明:连结.
分别为的中点,∴.…2分
又,且.
∴四边形是平行四边形,
即.………………3分
∴.………………4分
∵,且由知.
∴,∴,∴.………………6分
因是底面圆的直径,得,且,
∴即为四棱锥的高. ………………………………7分
设圆柱高为,底半径为,则,,
∴.………………………………9分
解一:由可知,可分别以为
坐标轴建立空间直角标系,如图设,
则,,,
从而,
,由题设知是面的法向量,
设所求的角为.…………………………………12分
则.………………………………14分
解二:作过的母线,连结,则是上底
面圆的直径,连结,得,
又,∴,连结,
则为与面所成的角,
设,则,.(12分),
在中,.(14分)
19.解:(1)男生被抽取人数为3人,女生被抽取人数为2人.……………………………2分
选取的两名学生都是女生的概率,所求的概率为.……………6分
(2).…………………9分
用表示3个男生中考前心理状态好的人数,表示2个女生中考前心理状态好的人数,
则
∴. …………………………………………………………14分
法二:的可能取值为0.1.2.3.4.5. ……………………8分
P(=0)=
E=2.8 ……………………14分
21.解析:(Ⅰ)
①时, ∴在(—1,+)上是增函数 ……………1分
②当时,在上递增,在单调递减. …………4分
(Ⅱ)由(Ⅰ)知,在上单调递增,在上单调递减
又
∴
∴当时,方程有两解 ………………8分
(Ⅲ)要证:只需证
只需证:
设, 则………………10分
由(Ⅰ)知在单调递减 ………………12分
∴,即是减函数,而m>n
∴,故原不等式成立。 ………………14分
8 9
1 2 3 4 6 7 8 9
0 1 1 3 3 3 5 7 8 8
0 1 2 2 3 4 8 9
0 1
第7题图
x
y
z
2011—2012学年度普通高中毕业班教学质量
数学试题(理科)
本试卷共21小题,满分150分.考试时间120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号.试室号.座位号填写在答题卡上.用2B铅笔将试卷类型(A)填涂在答题卡相应位置上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
4.作答选做题时.请先用2B铅笔填涂选做题的题号对应的信息点,再作答。漏涂.错涂.多涂的.答案无效.
5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
参考公式: 柱体的体积公式V=sh,其中S是柱体的底面积,h为柱体的高.
棱锥的体积公式,其中S是棱锥体的底面积,h为棱锥体的高.
第 一 卷
一、选择题(每小题5分,共40分,每小题给出的四个选项中,只有一项符合题目要求)
1.复数在复平面上对应的点的坐标是 ( )
A. B. C. D.
2.已知等比数列{an}的公比q为正数,且2a3+a4=a5,则q的值为 ( )
A. B.2 C. D.3
3.下列判断错误的是 ( )
A.“”是“”的充分不必要条件
B.命题“”的否定是“”
C.设随机变量
D.若为假命题,则p,q均为假命题
4.右图是某篮球运动员在一个赛季的30场比赛
中得分的茎叶图,则得分的中位数与众数分别
为( )
A.3与3
B.23与3
C.3与23
D.23与23
A. B. C. D.
6.若一个三位数的十位数字比个位数字和百位数字都大,称这个数为 “伞数”。现从1,2,3,4,5,6这六个数字中取3个数,组成无重复数字的三位数,其中“伞数”有 ( )
A.120个 B.80个 C.40个 D.20个
7.如图,半圆的直径AB=6,O为圆心,C为半圆上不同于
A.B的任意一点,若P为半径OC上的动点,
则的最小值是( )
A. B. C. D.
8.用表示非空集合A中的元素个数,定义,若,,且,由的所有可能值构成的集合是S,那么等于( )
A.4 B. 3 C.2 D. 1
第 二 卷
二、填空题:(本大题共6小题,考生作答6小题,每小题5分,满分30分.)
(一)必做题(9~13题)
9.设函数,若,则________.
10.函数y=的定义域为____________.
11.展开式中的系数是 .
12.已知某程序框图如图所示,则执行该程序后输出
的结果是___________________.
13.已知m,n是两条不同的直线,是一个平面,
有下列四个命题:
① 若,则;
② 若,则;
③ 若,则;
④ 若,则. 第12题图
其中真命题的序号有______________.
(请将真命题的序号都填上)
(二)选做题(14~15题,考生只能从中选做一题)
14.(几何证明选讲选做题)如图,为⊙O的直径,C为
⊙O上一点,和过的切线互相垂直,垂足为P,
过B的切线交过C的切线于,交⊙O于Q,
若,,则PQ·PB= .
15.(坐标系与参数方程选做题)在极坐标系(ρ,θ)()中,曲线与的交点的极坐标为_____________.
三、解答题:(本大题共6小题,满分80分.)
16.(本小题满分12分)已知函数.
(Ⅰ)求函数的最小值和最小正周期;
(Ⅱ)已知内角的对边分别为,且,若向量与共线,求的值.
17.(本小题满分12分)已知函数f(x)=;
(Ⅰ)证明:函数f(x)在上为减函数;
(Ⅱ)是否存在负数,使得成立,若存在求出;若不存在,请说明理由。
18.(本小题满分14分)如图,为圆柱的母线,是底面圆的直径,
分别是的中点,DE⊥面CBB1.
(Ⅰ)证明:DE //面ABC;
(Ⅱ)求四棱锥与圆柱的体积比;
(Ⅲ)若,求与面所成角的正弦值.
19.(本小题满分14分)
已知汕头市某学校高中部某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查。
(Ⅰ)若要从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;
(Ⅱ)若男学生考前心理状态好的概率为0.6,女学生考前心理状态好的概率为0.5, 表示抽取的5名学生中考前心理状态好的人数,求P(=1)及E.
20.(本小题满分14分)
已知数列满足:
(Ⅰ)探究数列是等差数列还是等比数列,并由此求数列的通项公式;
(Ⅱ)求数列的前n项和
21.(本小题满分14分) 设函数
(Ⅰ)求的单调区间;
(Ⅱ)当时,若方程在上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,.
参考答案
一、选择题 1.A 2.B 3.D 4.D 5.C 6.C 7.A 8.B
7.A 解析:设 , 则
, 所以
8. B 解析:依题意知或,当时,方程恰有1个根,有,得;当时,方程恰有3个根,有,得;故的可能值有3个,故.
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
9. 3 10. (3,4 】 11. 12. 13. ②③
14. 3 15.
三、解答题
①……………………9分
又c=3,由余弦定理,得 ②……………………10分
解方程组①②,得 ……………………12分
17. 解:(1)任取,且
∵ …………4分
∴函数在上为减函数 ………………………6分
另解:如果应用导数证明请相应给分
(2)不存在 ……………………………………………………7分
假设存在负数,使得成立,则 即
………………………10分
与矛盾,
所以不存在负数,使得成立。 ……………………………12分
另解:,由得: 或但,
所以不存在。
18. 解:证明:连结.
分别为的中点,∴.…2分
又,且.
∴四边形是平行四边形,
即.………………3分
∴.………………4分
∵,且由知.
∴,∴,∴.………………6分
因是底面圆的直径,得,且,
∴即为四棱锥的高. ………………………………7分
设圆柱高为,底半径为,则,,
∴.………………………………9分
解一:由可知,可分别以为
坐标轴建立空间直角标系,如图设,
则,,,
从而,
,由题设知是面的法向量,
设所求的角为.…………………………………12分
则.………………………………14分
解二:作过的母线,连结,则是上底
面圆的直径,连结,得,
又,∴,连结,
则为与面所成的角,
设,则,.(12分),
在中,.(14分)
19.解:(1)男生被抽取人数为3人,女生被抽取人数为2人.……………………………2分
选取的两名学生都是女生的概率,所求的概率为.……………6分
(2).…………………9分
用表示3个男生中考前心理状态好的人数,表示2个女生中考前心理状态好的人数,
则
∴. …………………………………………………………14分
法二:的可能取值为0.1.2.3.4.5. ……………………8分
P(=0)=
E=2.8 ……………………14分
21.解析:(Ⅰ)
①时, ∴在(—1,+)上是增函数 ……………1分
②当时,在上递增,在单调递减. …………4分
(Ⅱ)由(Ⅰ)知,在上单调递增,在上单调递减
又
∴
∴当时,方程有两解 ………………8分
(Ⅲ)要证:只需证
只需证:
设, 则………………10分
由(Ⅰ)知在单调递减 ………………12分
∴,即是减函数,而m>n
∴,故原不等式成立。 ………………14分
8 9
1 2 3 4 6 7 8 9
0 1 1 3 3 3 5 7 8 8
0 1 2 2 3 4 8 9
0 1
第7题图
x
y
z
同课章节目录
