4.3 角 (复习课件)
图片预览









文档简介
(共33张PPT)
§4.3 角
4.3.1 角
第1部分 角的有关概念
第2部分 角的度量
4.3.2 角的比较与运算
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
第2部分 方位角
【要点归纳】
1.角的定义:
(1)有 的两条 组成的图形叫做角.
(2)由一条射线 的图形叫做角.
2.角的表示方法:
(1)用三个大写英文字母表示任意一个角;
(2)用一个大写英文字母表示一个独立的角(在一顶点处只有一个角);
(3)加弧线、标数字表示一个角;
(4)加弧线、标小写希腊字母表示一个角.
4.3.1 角 第1部分 角的有关概念
3.角的分类
(1)直角:等于 的角叫直角.
(2)平角:等于 的角或一条射线绕着端点旋转,当终止位置与起始位置成一条直线时,所成的角叫做平角.
(3)周角:等于 的角或一条射线绕着端点旋转,当终止位置又回到起始位置时所成的角叫做周角.
(4)锐角:小于 大于 的角叫锐角.
(5)钝角:大于 而小于 的角叫钝角.
4.3.1 角 第1部分 角的有关概念
【题型归类】
类型一、角的有关概念
例1.下列说法正确有( )
两条射线组成的图形叫做角;
平角是一条直线;
周角是一条射线;
角的两边越长,角就越大;
∠AOB与∠BOA表示同一个角.
A.1个 B.2个 C.3个 D.4个
4.3.1 角 第1部分 角的有关概念
类型二、角的表示方法
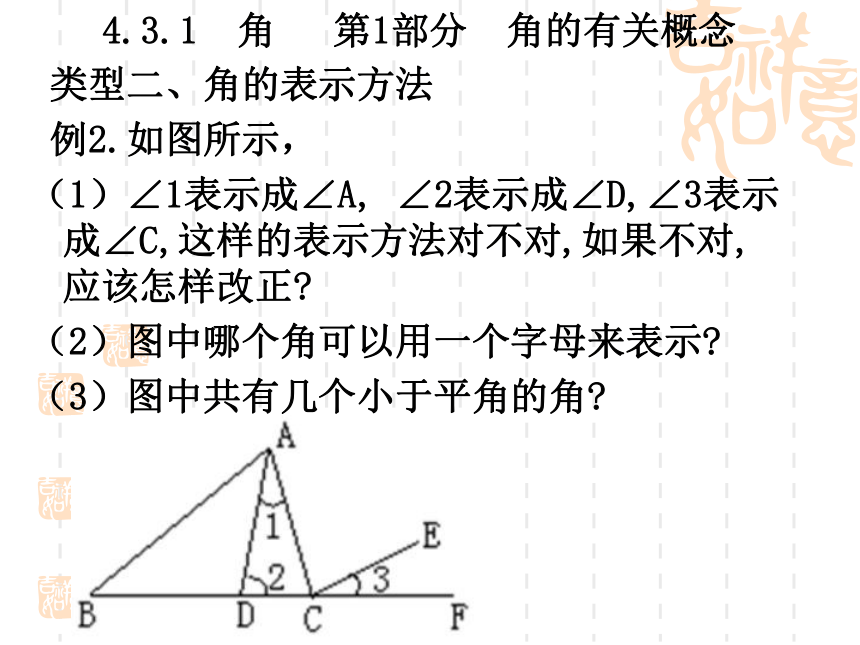
例2.如图所示,
(1)∠1表示成∠A, ∠2表示成∠D,∠3表示成∠C,这样的表示方法对不对,如果不对,应该怎样改正
(2)图中哪个角可以用一个字母来表示
(3)图中共有几个小于平角的角
4.3.1 角 第1部分 角的有关概念
类型三、角的计数
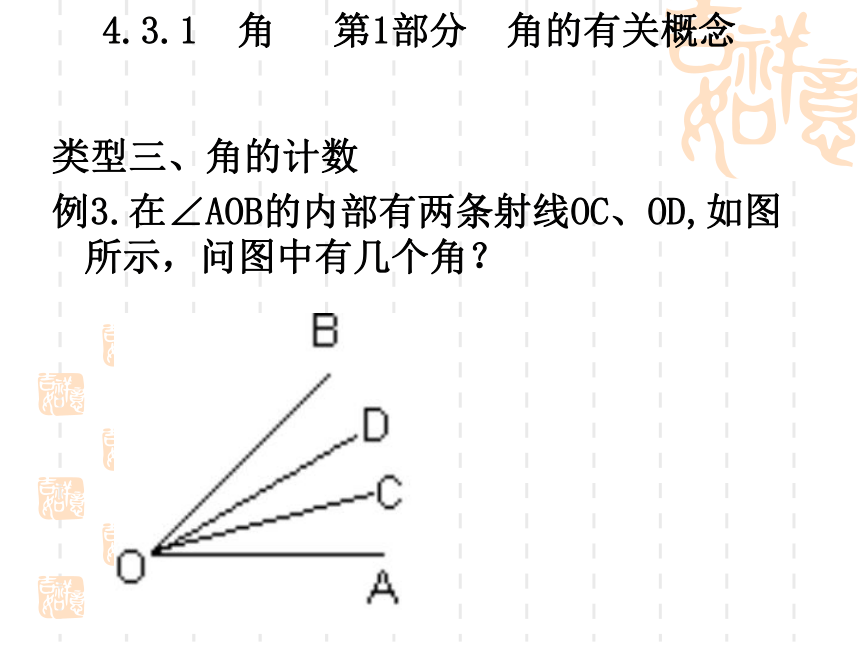
例3.在∠AOB的内部有两条射线OC、OD,如图所示,问图中有几个角?
4.3.1 角 第1部分 角的有关概念
【易错点示】
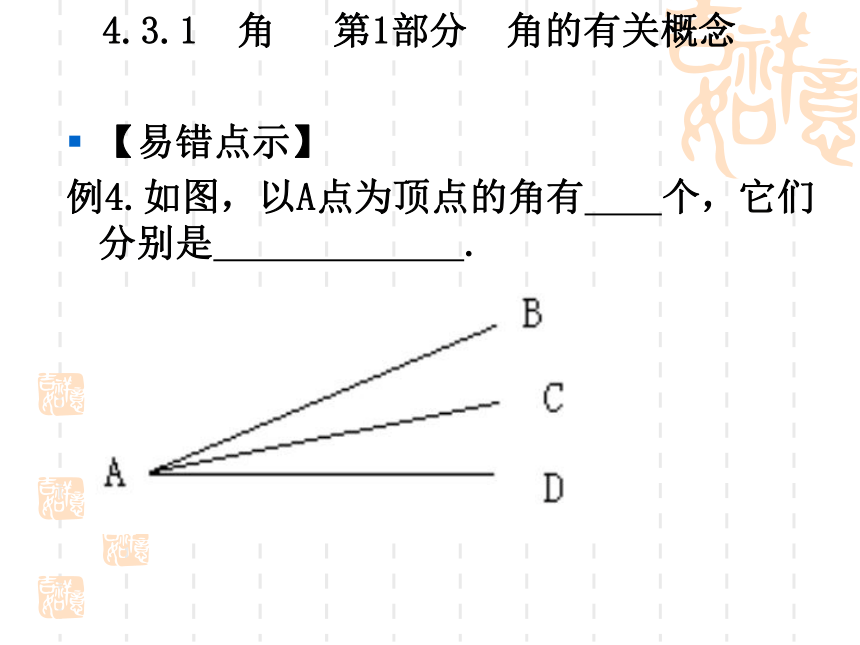
例4.如图,以A点为顶点的角有 个,它们分别是 .
4.3.1 角 第1部分 角的有关概念
4.3.1 角
第2部分 角的度量
【要点归纳】
1.度、分、秒是常用的角的度量单位. 1°= ,1′= .
2.借助三角尺,可以画出30°、45°、60°、90°等特殊角,借助量角器,可以画出任意给定度数的角.
4.3.1 角 第2部分 角的度量
【题型归类】
类型一、度、分、秒单位间的换算
例1.计算:
⑴1.45°等于多少分 等于多少秒
⑵1800″等于多少分 等于多少度
4.3.1 角 第2部分 角的度量
类型二、角度的计算
例2. 计算:
(1)180°-(48°39′40″+67°41′35″)
(2)23°41′34″×3
(3)109°11′4″÷7
4.3.1 角 第2部分 角的度量
类型三、钟表上的角度问题
例3. 在时刻8:30,时钟上的时针和分针之间的夹角为( )度.
A. 85 B. 75 C. 70 D. 60
4.3.1 角 第2部分 角的度量
【易错点示】
例4.纸上有一个9°的角,如果用十倍放大镜观察这个角,就会得到一个 度的角.
4.3.1 角 第2部分 角的度量
4.3.2 角的比较与运算
【要点归纳】
1.角的大小可以有两种比较方法: 和 .
(1)重叠比较法:在比较角的大小的过程中,要让角的顶点和角的一条边都重合,看另一条边落在角内还是角外.
(2)度量法:因为角可以用量角器来量出度数,度数大的角大于度数小的角,通过角的度数来比较角的大小.
2.角的和、差、倍、分运算也可以有两种方法:作图法和度量计算法.
(1)作图法:在图中作出两个角的和、差、倍、分.
(2)度量计算法.
4.3.2 角的比较与运算
3.角平分线定义:一条射线把一个角分成 的角,这条射线叫做这个角的平分线.
角平分线是一条 .
4.如图,射线OB是∠AOC的平分线,则有
∠AOB= = 或 2∠AOB=2 = .
4.3.2 角的比较与运算
【题型归类】
类型一、角平分线的识别
例1.已知∠AOB,下列能说明射线OC是∠AOB的角平分线的是( )
A. ∠AOB=2∠AOC B. ∠BOC=
C. ∠AOC=∠BOC D. ∠AOC=∠AOB
4.3.2 角的比较与运算
类型二、角的和、差、倍、分的计算
例2.如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD,
∠COE=72°,求∠EOB的度数.
4.3.2 角的比较与运算
类型三、与角平分线有关的计算题
例3.如图所示,ON是∠BOC的平分线,OM是∠AOC的平分线,如果∠AOC=28°,∠BOC=42°,
(1)求∠MON的度数?
(2)当射线OC在∠AOB的内部绕点O转动,那么射线OM、ON的位置是否发生变化?
(3)∠MON的大小是否发生变化?如果不变,请说出其度数,如果变化,请说出变化范围.
4.3.2 角的比较与运算
【易错点示】
例4.已知具有公共顶点的两个角∠AOB和∠BOC,且∠AOB=70°,∠BOC=30°,求∠AOC的度数.
4.3.2 角的比较与运算
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【要点归纳】
1.如果两个角的和等于 ,那么这两个角互为余角,锐角α的余角是 .
2.如果两个角的和等于 ,那么这两个角互为补角,角α的补角是 .
3.互余、互补角的性质
等角或同角的余角 .
等角或同角的补角 .
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【题型归类】
类型一、互余、互补两角的概念
例1.
A.4个 B.3个 C.2个 D.1个
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
类型二、作已知角的余角或补角
例2. 如图所示,已知钝角∠α,画出它的补角和它的补角的余角.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
类型三、求一个角的余角或补角
例3.一个角的余角比它的补角的少20°,求这个角的度数.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【易错点示】
例4.下列描述正确的是( )
A.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补.
B.若∠1=90°-∠2,那么∠1与∠2互为余角.
C.互补的两个角一定是一个锐角,一个钝角.
D.任何角都有余角.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
4.3.3 余角和补角
第2部分 方位角
【要点归纳】
1.在现实生活中,有一种角经常用于航空、航海,测绘中领航员常用地图和罗盘进行这种角的测定,这就是 .
2.方位角就是表示方向的角,这种角以正北,正南方向为基准描述物体的方向,如“北偏东300”,“南偏西400”等,方位角不能以正 ,正 为基准,如不能说成“东偏北600,西偏南500”等,但有时如北偏东450时,我们可以说成 方向.
4.3.3 余角和补角 第2部分 方位角
【题型归类】
类型一、方位角
例1.指出图中的射线OA、OB、OC、OD、OE、OF所表示的方位角.
4.3.3 余角和补角 第2部分 方位角
类型二、方位角的作图
例2.某哨兵上午8时测得一艘船的位置在哨所A的南偏西300的B处,距哨所10km的地方,上午10时,测得该船在哨所的北偏东600,距哨所8km的C处.
(1)请按比例尺1:200000画出图形;
(2)通过测量计算,确定船航行的方向和进度.
4.3.3 余角和补角 第2部分 方位角
类型三、方位角的实际应用
例3.如图所示,一只蚂蚁从O点出发,沿北偏东45°的方向爬行2.5cm,碰到障碍物(记作B)后折向北偏西60°的方向爬行3cm(此时位置记作C点).
(1)画出蚂蚁的爬行路线;
(2)求出∠OBC的度数.
4.3.3 余角和补角 第2部分 方位角
【易错点示】
例4.如图,由 点B观测点A的方向是 .
4.3.3 余角和补角 第2部分 方位角
§4.3 角
4.3.1 角
第1部分 角的有关概念
第2部分 角的度量
4.3.2 角的比较与运算
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
第2部分 方位角
【要点归纳】
1.角的定义:
(1)有 的两条 组成的图形叫做角.
(2)由一条射线 的图形叫做角.
2.角的表示方法:
(1)用三个大写英文字母表示任意一个角;
(2)用一个大写英文字母表示一个独立的角(在一顶点处只有一个角);
(3)加弧线、标数字表示一个角;
(4)加弧线、标小写希腊字母表示一个角.
4.3.1 角 第1部分 角的有关概念
3.角的分类
(1)直角:等于 的角叫直角.
(2)平角:等于 的角或一条射线绕着端点旋转,当终止位置与起始位置成一条直线时,所成的角叫做平角.
(3)周角:等于 的角或一条射线绕着端点旋转,当终止位置又回到起始位置时所成的角叫做周角.
(4)锐角:小于 大于 的角叫锐角.
(5)钝角:大于 而小于 的角叫钝角.
4.3.1 角 第1部分 角的有关概念
【题型归类】
类型一、角的有关概念
例1.下列说法正确有( )
两条射线组成的图形叫做角;
平角是一条直线;
周角是一条射线;
角的两边越长,角就越大;
∠AOB与∠BOA表示同一个角.
A.1个 B.2个 C.3个 D.4个
4.3.1 角 第1部分 角的有关概念
类型二、角的表示方法
例2.如图所示,
(1)∠1表示成∠A, ∠2表示成∠D,∠3表示成∠C,这样的表示方法对不对,如果不对,应该怎样改正
(2)图中哪个角可以用一个字母来表示
(3)图中共有几个小于平角的角
4.3.1 角 第1部分 角的有关概念
类型三、角的计数
例3.在∠AOB的内部有两条射线OC、OD,如图所示,问图中有几个角?
4.3.1 角 第1部分 角的有关概念
【易错点示】
例4.如图,以A点为顶点的角有 个,它们分别是 .
4.3.1 角 第1部分 角的有关概念
4.3.1 角
第2部分 角的度量
【要点归纳】
1.度、分、秒是常用的角的度量单位. 1°= ,1′= .
2.借助三角尺,可以画出30°、45°、60°、90°等特殊角,借助量角器,可以画出任意给定度数的角.
4.3.1 角 第2部分 角的度量
【题型归类】
类型一、度、分、秒单位间的换算
例1.计算:
⑴1.45°等于多少分 等于多少秒
⑵1800″等于多少分 等于多少度
4.3.1 角 第2部分 角的度量
类型二、角度的计算
例2. 计算:
(1)180°-(48°39′40″+67°41′35″)
(2)23°41′34″×3
(3)109°11′4″÷7
4.3.1 角 第2部分 角的度量
类型三、钟表上的角度问题
例3. 在时刻8:30,时钟上的时针和分针之间的夹角为( )度.
A. 85 B. 75 C. 70 D. 60
4.3.1 角 第2部分 角的度量
【易错点示】
例4.纸上有一个9°的角,如果用十倍放大镜观察这个角,就会得到一个 度的角.
4.3.1 角 第2部分 角的度量
4.3.2 角的比较与运算
【要点归纳】
1.角的大小可以有两种比较方法: 和 .
(1)重叠比较法:在比较角的大小的过程中,要让角的顶点和角的一条边都重合,看另一条边落在角内还是角外.
(2)度量法:因为角可以用量角器来量出度数,度数大的角大于度数小的角,通过角的度数来比较角的大小.
2.角的和、差、倍、分运算也可以有两种方法:作图法和度量计算法.
(1)作图法:在图中作出两个角的和、差、倍、分.
(2)度量计算法.
4.3.2 角的比较与运算
3.角平分线定义:一条射线把一个角分成 的角,这条射线叫做这个角的平分线.
角平分线是一条 .
4.如图,射线OB是∠AOC的平分线,则有
∠AOB= = 或 2∠AOB=2 = .
4.3.2 角的比较与运算
【题型归类】
类型一、角平分线的识别
例1.已知∠AOB,下列能说明射线OC是∠AOB的角平分线的是( )
A. ∠AOB=2∠AOC B. ∠BOC=
C. ∠AOC=∠BOC D. ∠AOC=∠AOB
4.3.2 角的比较与运算
类型二、角的和、差、倍、分的计算
例2.如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD,
∠COE=72°,求∠EOB的度数.
4.3.2 角的比较与运算
类型三、与角平分线有关的计算题
例3.如图所示,ON是∠BOC的平分线,OM是∠AOC的平分线,如果∠AOC=28°,∠BOC=42°,
(1)求∠MON的度数?
(2)当射线OC在∠AOB的内部绕点O转动,那么射线OM、ON的位置是否发生变化?
(3)∠MON的大小是否发生变化?如果不变,请说出其度数,如果变化,请说出变化范围.
4.3.2 角的比较与运算
【易错点示】
例4.已知具有公共顶点的两个角∠AOB和∠BOC,且∠AOB=70°,∠BOC=30°,求∠AOC的度数.
4.3.2 角的比较与运算
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【要点归纳】
1.如果两个角的和等于 ,那么这两个角互为余角,锐角α的余角是 .
2.如果两个角的和等于 ,那么这两个角互为补角,角α的补角是 .
3.互余、互补角的性质
等角或同角的余角 .
等角或同角的补角 .
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【题型归类】
类型一、互余、互补两角的概念
例1.
A.4个 B.3个 C.2个 D.1个
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
类型二、作已知角的余角或补角
例2. 如图所示,已知钝角∠α,画出它的补角和它的补角的余角.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
类型三、求一个角的余角或补角
例3.一个角的余角比它的补角的少20°,求这个角的度数.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
【易错点示】
例4.下列描述正确的是( )
A.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补.
B.若∠1=90°-∠2,那么∠1与∠2互为余角.
C.互补的两个角一定是一个锐角,一个钝角.
D.任何角都有余角.
4.3.3 余角和补角
第1部分 余角和补角有关概念和计算
4.3.3 余角和补角
第2部分 方位角
【要点归纳】
1.在现实生活中,有一种角经常用于航空、航海,测绘中领航员常用地图和罗盘进行这种角的测定,这就是 .
2.方位角就是表示方向的角,这种角以正北,正南方向为基准描述物体的方向,如“北偏东300”,“南偏西400”等,方位角不能以正 ,正 为基准,如不能说成“东偏北600,西偏南500”等,但有时如北偏东450时,我们可以说成 方向.
4.3.3 余角和补角 第2部分 方位角
【题型归类】
类型一、方位角
例1.指出图中的射线OA、OB、OC、OD、OE、OF所表示的方位角.
4.3.3 余角和补角 第2部分 方位角
类型二、方位角的作图
例2.某哨兵上午8时测得一艘船的位置在哨所A的南偏西300的B处,距哨所10km的地方,上午10时,测得该船在哨所的北偏东600,距哨所8km的C处.
(1)请按比例尺1:200000画出图形;
(2)通过测量计算,确定船航行的方向和进度.
4.3.3 余角和补角 第2部分 方位角
类型三、方位角的实际应用
例3.如图所示,一只蚂蚁从O点出发,沿北偏东45°的方向爬行2.5cm,碰到障碍物(记作B)后折向北偏西60°的方向爬行3cm(此时位置记作C点).
(1)画出蚂蚁的爬行路线;
(2)求出∠OBC的度数.
4.3.3 余角和补角 第2部分 方位角
【易错点示】
例4.如图,由 点B观测点A的方向是 .
4.3.3 余角和补角 第2部分 方位角
